Trigonometric Functions | The Complete SAT Course - Class 10 PDF Download
Trigonometric functions are the basic six functions that have a domain input value as an angle of a right triangle, and a numeric answer as the range. The trigonometric function (also called the 'trig function') of f(x) = sinθ has a domain, which is the angle θ given in degrees or radians, and a range of [-1, 1]. Similarly we have the domain and range from all other functions. Trigonometric functions are extensively used in calculus, geometry, algebra.
Here in the below content, we shall aim at understanding the trigonometric functions across the four quadrants, their graphs, the domain and range, the formulas, and the differentiation, integration of trigonometric functions. We will solve a few examples using these six trig functions for a better understanding of them and their applications.
What are Trigonometric Functions?
There are six basic trigonometric functions used in Trigonometry. These functions are trigonometric ratios. The six basic trigonometric functions are sine function, cosine function, secant function, co-secant function, tangent function, and co-tangent function. The trigonometric functions and identities are the ratio of sides of a right-angled triangle. The sides of a right triangle are the perpendicular side, hypotenuse, and base, which are used to calculate the sine, cosine, tangent, secant, cosecant, and cotangent values using trigonometric formulas.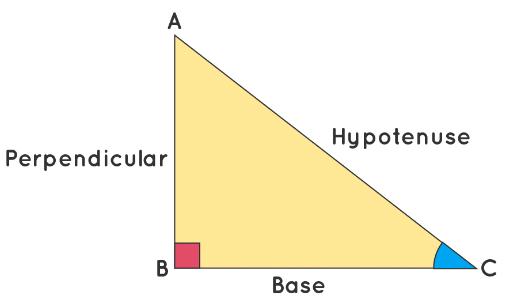
Trigonometric Functions Formulas
We have certain formulas to find the values of the trig functions using the sides of a right-angled triangle. To write these formulas, we use the abbreviated form of these functions. Sine is written as sin, cosine is written as cos, tangent is denoted by tan, secant is denoted by sec, cosecant is abbreviated as cosec, and cotangent is abbreviated as cot. The basic formulas to find the trigonometric functions are as follows:
- sin θ = Perpendicular/Hypotenuse
- cos θ = Base/Hypotenuse
- tan θ = Perpendicular/Base
- sec θ = Hypotenuse/Base
- cosec θ = Hypotenuse/Perpendicular
- cot θ = Base/Perpendicular
As we can observe from the above-given formulas, sine and cosecant are reciprocals of each other. Similarly, the reciprocal pairs are cosine and secant, and tangent and cotangent.
Trigonometric Functions Values
The trigonometric functions have a domain θ, which is in degrees or radians. Some of the principal values of θ for the different trigonometric functions are presented below in a table. These principal values are also referred to as standard values of trig functions at specific angles and are frequently used in calculations. The principal values of trigonometric functions have been derived from a unit circle. These values also satisfy all the trigonometric formulas.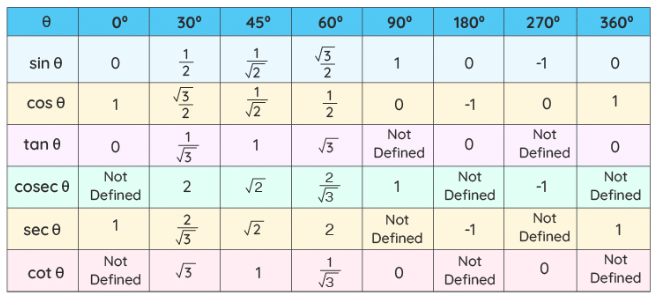
Trigonometric Functions in Four Quadrants
The angle θ is an acute angle (θ < 90°) and is measured with reference to the positive x-axis, in the anticlockwise direction. Further, these trig functions have different numeric signs (+ or -) in the different quadrants, which are based on the positive or negative axis of the quadrant. The trigonometric functions of Sinθ, Cosecθ are positive in quadrants I and II, and are negative in quadrants III and IV. All the trigonometric functions have a positive range in the first quadrant. The trigonometric functions Tanθ, Cotθ are positive only in Quadrants I and III, and the trigonometric ratios of Cosθ, Secθ are positive only in quadrants I and IV.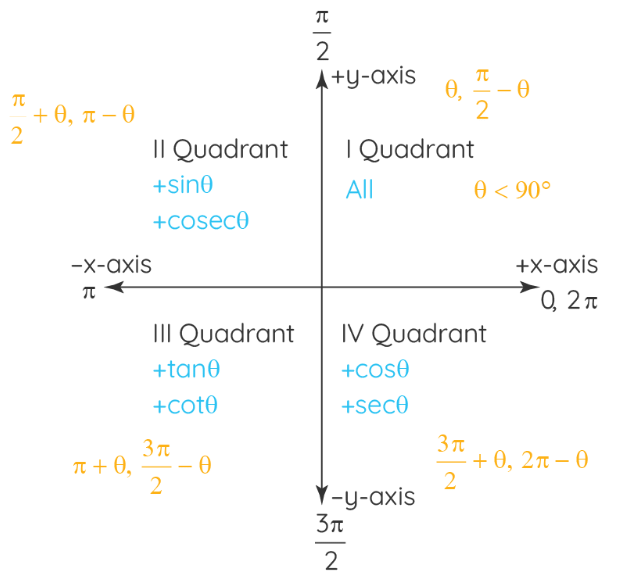
The trigonometric functions have values of θ, (90° - θ) in the first quadrant. The cofunction identities provide the interrelationship between the different complementary trigonometric functions for the angle (90° - θ).
- sin(90°−θ) = cos θ
- cos(90°−θ) = sin θ
- tan(90°−θ) = cot θ
- cot(90°−θ) = tan θ
- sec(90°−θ) = cosec θ
- cosec(90°−θ) = sec θ
The domain θ value for different trigonometric function in the second quadrant is (π/2 + θ, π - θ), in the third quadrant is (π + θ, 3π/2 - θ), and in the fourth quadrant is (3π/2 + θ, 2π - θ). For π/2, 3π/2 the trigonometric values changes as their complementary ratios such as Sinθ⇔Cosθ, Tanθ⇔Cotθ, Secθ⇔Cosecθ. For π, 2π the trigonometric values remain the same. The changing trigonometric ratios in different quadrants and angles can be understood from the below table.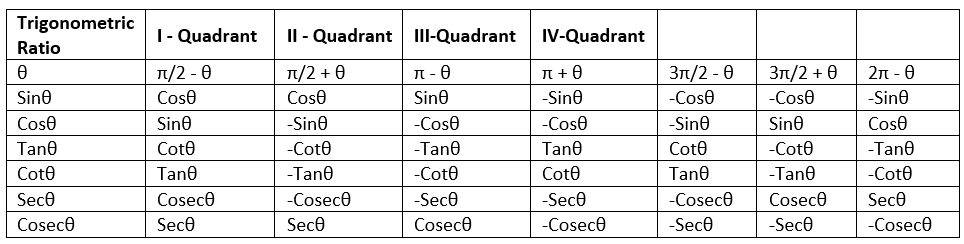
Trigonometric Functions Graph
The graphs of trigonometric functions have the domain value of θ represented on the horizontal x-axis and the range value represented along the vertical y-axis. The graphs of Sinθ and Tanθ pass through the origin and the graphs of other trigonometric functions do not pass through the origin. The range of Sinθ and Cosθ is limited to [-1, 1]. The range of infinite values is presented as drawn beside the dotted lines.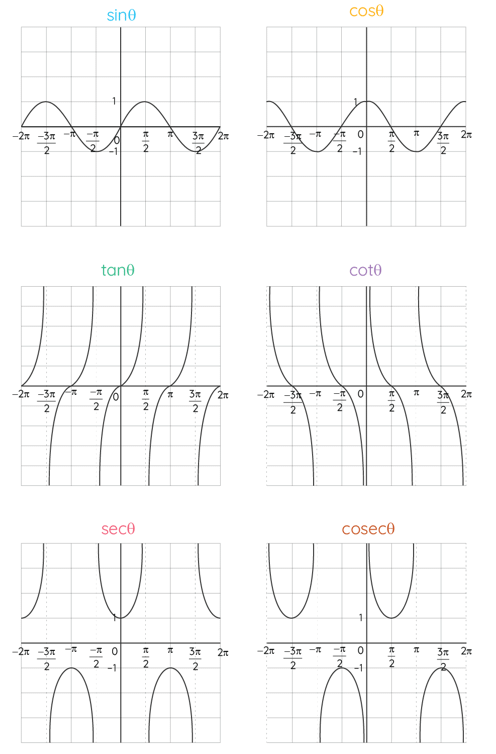
Domain and Range of Trigonometric Functions
The value of θ represents the domain of the trigonometric functions and the resultant value is the range of the trigonometric function. The domain values of θ are in degrees or radians and the range is a real number value. Generally, the domain of the trigonometric function is a real number value, but in certain cases, a few angle values are excluded because it results in a range as an infinite value. The trigonometric function are periodic functions. The below table presents the domain and range of the six trigonometric functions.
Trigonometric Functions Identities
The trigonometric functions identities are broadly divided into reciprocal identities, Pythagorean formulas, sum and difference of trig functions identities, formulas for multiple and sub-multiple angles, sum and product of identities. All of these below formulas can be easily derived using the ratio of sides of a right-angled triangle. The higher formulas can be derived by using the basic trigonometric function formulas. Reciprocal identities are used frequently to simplify trigonometric problems.
Reciprocal Identities
- cosec θ = 1/sin θ
- sec θ = 1/cos θ
- cot θ = 1/tan θ
- sin θ = 1/cosec θ
- cos θ = 1/sec θ
- tan θ = 1/cot θ
Pythagorean Identities
- Sin2θ + Cos2θ = 1
- 1 + Tan2θ = Sec2θ
- 1 + Cot2θ = Cosec2θ
Sum and Difference Identities
- sin(x+y) = sin(x)cos(y) + cos(x)sin(y)
- cos(x+y) = cos(x)cos(y) – sin(x)sin(y)
- tan(x+y) = (tan x + tan y)/ (1−tan x tan y)
- sin(x–y) = sin(x)cos(y) – cos(x)sin(y)
- cos(x–y) = cos(x)cos(y) + sin(x)sin(y)
- tan(x−y) = (tan x–tan y)/ (1+tan x tan y)
Half-Angle Identities
- sin A/2 = ±√[(1 - cos A) / 2]
- cos A/2 = ±√[(1 + cos A) / 2]
- tan A/2 = ±√[(1 - cos A) / (1 + cos A)] (or) sin A / (1 + cos A) (or) (1 - cos A) / sin A
Double Angle Identities
- sin(2x) = 2sin(x) cos(x) = [2tan x/(1+tan2 x)]
- cos(2x) = cos2(x)–sin2(x) = [(1-tan2 x)/(1+tan2 x)]
- cos(2x) = 2cos2(x)−1 = 1–2sin2(x)
- tan(2x) = [2tan(x)]/ [1−tan2(x)]
- cot(2x) = [cot2(x) - 1]/[2cot(x)]
- sec (2x) = sec2x/(2-sec2 x)
- cosec (2x) = (sec x. cosec x)/2
Triple Angle Identities
- Sin 3x = 3sin x – 4sin3x
- Cos 3x = 4cos3x - 3cos x
- Tan 3x = [3tanx-tan3x]/[1-3tan2x]
Product identities
- 2sinx⋅cosy=sin(x+y)+sin(x−y)
- 2cosx⋅cosy=cos(x+y)+cos(x−y)
- 2sinx⋅siny=cos(x−y)−cos(x+y)
Sum of Identities
- sinx+siny=2sin((x+y)/2) . cos((x−y)/2)
- sinx−siny=2cos((x+y)/2) . sin((x−y)/2)
- cosx+cosy=2cos((x+y)/2) . cos((x−y)/2)
- cosx−cosy=−2sin((x+y)/2 . sin((x−y)/2)
Inverse Trigonometric Functions
Inverse trigonometric functions are the inverse ratio of the basic trigonometric ratios. Here the basic trigonometric function of Sin θ = x, can be changed to Sin-1 x = θ. Here x can have values in whole numbers, decimals, fractions, or exponents. For θ = 30° we have θ = Sin-1 (1/2). All the trigonometric formulas can be transformed into inverse trigonometric function formulas.
Arbitrary Values: The inverse trigonometric ratio formula for arbitrary values is applicable for all the six trigonometric functions. For the inverse trigonometric functions of sine, tangent, cosecant, the negative of the values are translated as the negatives of the function. And for functions of cosecant, secant, cotangent, the negatives of the domain are translated as the subtraction of the function from the π value.
- Sin-1(-x) = -Sin-1x
- Tan-1(-x) = -Tan-1x
- Cosec-1(-x) = -Cosec-1x
- Cos-1(-x) = π - Cos-1x
- Sec-1(-x) = π - Sec-1x
- Cot-1(-x) = π - Cot-1x
The inverse trigonometric functions of reciprocal and complementary functions are similar to the basic trigonometric functions. The reciprocal relationship of the basic trigonometric functions, sine-cosecant, cos-secant, tangent-cotangent, can be interpreted for the inverse trigonometric functions. Also the complementary functions, since-cosine, tangent-cotangent, and secant-cosecant can be interpreted into:
Reciprocal Functions: The inverse trigonometric formula of inverse sine, inverse cosine, and inverse tangent can also be expressed in the following forms.
- Sin-1x = Cosec-11/x
- Cos-1x = Sec-11/x
- Tan-1x = Cot-11/x
Complementary Functions: The complementary functions of sine-cosine, tangent-cotangent, secant-cosecant, sum up to π/2.
- Sin-1x + Cos-1x = π/2
- Tan-1x + Cot-1x = π/2
- Sec-1x + Cosec-1x = π/2
Trigonometric Functions Derivatives
The differentiation of trigonometric functions gives the slope of the tangent of the curve. The differentiation of Sinx is Cosx and here on applying the x value in degrees for Cosx we can obtain the slope of the tangent of the curve of Sinx at a particular point. The formulas of differentiation of trigonometric functions are useful to find the equation of a tangent, normal, to find the errors in calculations.
- d/dx. Sinx = Cosx
- d/dx. Cosx = -Sinx
- d/dx. Tanx = Sec2x
- d/dx. Cotx = -Cosec2x
- d/dx.Secx = Secx.Tanx
- d/dx. Cosecx = - Cosecx.Cotx
Integration of Trigonometric Function
The integration of trigonometric functions is helpful to find the area under the graph of the trigonometric function. Generally, the area under the graph of the trigonometric function can be calculated with reference to any of the axis lines and within a defined limit value. The integration of trigonometric functions is helpful to generally find the area of irregularly shaped plane surfaces.
- ∫ cosx dx = sinx + C
- ∫ sinx dx = -cosx + C
- ∫ sec2x dx = tanx + C
- ∫ cosec2x dx = -cotx + C
- ∫ secx.tanx dx = secx + C
- ∫ cosecx.cotx dx = -cosecx + C
- ∫ tanx dx = log|secx| + C
- ∫ cotx.dx = log|sinx| + C
- ∫ secx dx = log|secx + tanx| + C
- ∫ cosecx.dx = log|cosecx - cotx| + C
|
433 videos|220 docs|166 tests
|





















