Hydraulic Similitude | Irrigation Engineering - Civil Engineering (CE) PDF Download
Introduction
Solutions of complicated problems in hydraulic engineering is simplified by model analysis. Model analysis is also required for predicting performance of hydraulic structures like dams and spillways, hydraulic machines such as turbines and pumps, structures, ships, aircrafts etc. The results of model studies represent the behaviour of prototype, if there is similitude or similarities between model and prototype. Three similarities required are:
- Geometric similarity
- Kinematic similarity
- Dynamic similarity
Geometric Similarity
Geometrically similar objects are similar in their shape. They differs only in their size. The ratio of any length of the prototype to the corresponding length in the model is same everywhere. The ratio is known as scale factor.
For perfect geometric similarity, roughness of surface also should be geometrically similar. But this is not easily attained.
If lm, bm, dm, hm, etc., are certain linear dimensions of the model and cp, lp, dp, hp, etc., are the corresponding linear dimensions of the prototype, condition for geometric similarity is,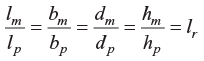
lr is called scale ratio or scale factor or model ratio
Area ratio, 
Volume ratio, 
Kinematic Similarity
Similarity of motion is called kinematic similarity. Kinematic similarity between prototype and model exists when the ratios of corresponding kinematic quantities such as velocity, acceleration, etc., at corresponding points are same.
Therefore, velocity ratios,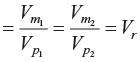
Similarly acceleration ratio,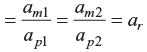
In terms of scale ratio,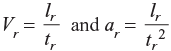
Where, tr = ratio of corresponding time intervals.
Geometric similarity is a pre-requisite for kinematic similarity. Also the directions of velocities in the model and prototype should be same.
Dynamic Similarity
Dynamic similarity is the similarity of masses and forces. The ratios of masses of corresponding fluid particles should be same. Similarly magnitudes of forces at corresponding points in each system should be in a fixed ratio. Therefore the ratio of magnitudes of any two forces in the prototype should be same as the magnitude ratio of the corresponding forces in the model. The different forces that may act on a fluid element are:
- Viscous force (Fv)
- Pressure force (Fp)
- Gravity force (Fg)
- Surface tension or capillary force (Fs)
- Elastic force (Fe) (due to compressibility)
Resultant of these forces causes acceleration of the fluid element which is opposed by the inertia force (Fi),
∴ FR = Fv + Fp + Fg + Fs + Fe
= –Fi and Fv + Fp + Fg + Fs + Fe + Fi = 0
For dynamic similarity, the ratio of these forces should be same for prototype and model. Generally Fi is taken as the common one to describe ratios.
For example,  etc.
etc.
For absolute dynamic similarity the ratios corresponding to all the forces should be same for model and prototype, but it is not possible to satisfy all these equations simultaneously. Therefore for practical cases ratio of the predominant force with inertia force is considered for dynamic similarity.
Various forces acting on a fluid element as mentioned above are functions of certain variables which can be classified into three:
- Linear dimension (l, d)
- Fluid properties (ρ , μ , σ , E)
- Kinematic and dynamic characteristics (v, p, g)
Various forces can be expressed in terms of the above as follows:
1. Viscous force,
Fv = Shear stress × Area
= μ × Velocity gradient × Area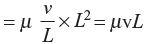
2. Pressure force,
Fp = Pressure intensity × Area
= pL2
3. Gravity force,
Fg = mg = ρL3g
4. Surface tension force,
Fs = Surface tension × Length
= σL
5. Elastic force,
Fe = Stress × Area
= Strain × Modulus of elasticity × Area
= EL2
6. Inertia force,
Fi = Mass × Acceleration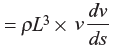
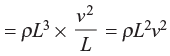
|
7 videos|49 docs|31 tests
|















