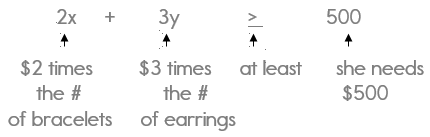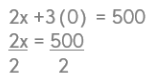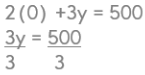Systems of Linear Inequalities Word Problems | The Complete SAT Course - Class 10 PDF Download
As you get further into Algebra 1, you will find that the real world problems become more complex. They have more questions to be answered and require more steps to find the solution.
When you get into systems of inequalities, this is especially true because you are dealing with two inequalities. But... don't let that intimidate you! You have all the skills that you need to solve these problems. Take one step at a time and think about what you need in order to answer the question. Read through my example very carefully, and study how I performed each step. Pay careful attention to the key words (highlighted words) and how each inequality was written based on the problem.
Then complete the practice problems.
Example 1: Systems of Inequalities Word Problem
Sarah is selling bracelets and earrings to make money for summer vacation. The bracelets cost $2 and earrings cost $3. She needs to make at least $500.
- Write an inequality to represent the income from the jewelry sold.
- Sarah knows that she will see more than 50 bracelets. Write an inequality to represent this situation.
- Graph the two inequalities and shade the intersection.
- Identify a solution. How many bracelets and earrings can Sarah sell?
Step 1: Highlight the important information in the problem.
Sarah is selling bracelets and earrings to make money for summer vacation. The bracelets cost $2 and earrings cost $3. She needs to make at least $500.
Step 2: Identify your variables. Think about what you don't know and need to know to solve the problem.
Let x = the number of bracelets sold.
Let y = the number of earrings sold.
Step 3: Write an inequality to represent the income form the jewelry sold. 2x + 3y ≥ 500
Here's how I came up with this inequality.Step 4: Sarah knows that she will sell more than 50 bracelets. Write an inequality to represent this situation.
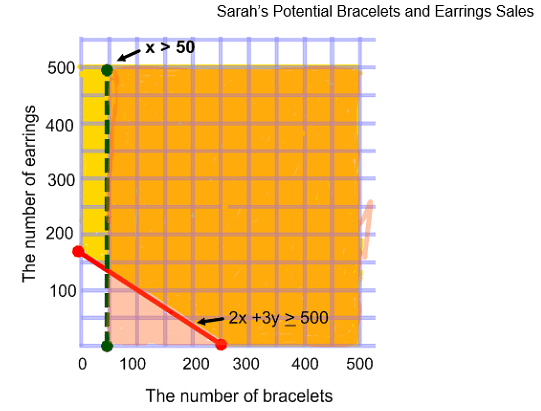
x > 50Step 5: Graph the two inequalities and shade the intersection.
In order to graph 2x +3y ≥ 500, we will need to find the x and y intercept.
So, to find the x intercept, we will let y = 0.
x = 250 (on the x axis, I plotted my point on 250)
To find the y intercept, we will let x = 0.
Y = 166.67 (We will have to estimate where this point is on the y-axis. I know it’s a little above the 150 mark)Then we can draw our line and determine which side to shade. Since 2x + 3y is greater than 500, I know that I can shade above the line. I can double check by using a test point. If I substitute (0,0) here’s what happens:
2x +3y ≥ 500
2(0) +3(0) ≥ 500
0 ≥ 500
Since 0 is not greater than or equal to 500, I am not going to shade the side that contains (0,0). I’ll shade above the red line.
To graph x > 50. we know from the last lesson, that this is a vertical line. Since x is greater than 50. we will shade to the right of the line.The solution to this system of inequalities is the orange shaded region.
Step 6: Identify a solution. How many bracelets and earrings could Sarah sell?
(200, 200) Sarah could sell 200 bracelets and 200 pairs of earrings.
For most real world problems, it will be easiest to graph the inequalities using the x and y intercepts. Make sure that you scale your grid so that both inequalities can be graphed on the same grid.
Here's a few tips to help you as you work through your word problems.
Steps for Solving a System of Inequalities Word Problem
- Read the problem and highlight important information.
- Identify the variables.
- Find one piece of information in the problem that you can use to write an inequality.
- Find a different piece of information that you can use to write a second inequality.
- Graph both inequalities on a grid. Make sure you use appropriate boundary lines and shade the correct half plane for each inequality.
- Identify the intersection of the two inequalities and answer the questions that pertain to the problem.
|
433 videos|220 docs|166 tests
|