Rules of Inference

What are Rules of Inference for?

Mathematical logic provides formal tools to construct and verify proofs. A proof is a valid argument that determines the truth of a statement from other statements. An argument is a finite sequence of statements in which the final statement is the conclusion and the preceding statements are the premises (or hypotheses). The symbol ∴ (read therefore) is often used to mark the conclusion. An argument is valid when the conclusion follows from the premises in such a way that it is impossible for all premises to be true and the conclusion false.

Rules of Inference are standard, sound templates that allow one to derive new statements (conclusions) from given statements (premises). Each rule shows a pattern of premises that guarantees a particular conclusion; using these rules preserves truth when applied correctly.

Table of Rules of Inference

Addition

Logical form: P / ∴ P ∨ Q

Explanation: From a single true proposition P one may infer the disjunction P ∨ Q for any proposition Q. This is truth-preserving because if P is true then the disjunction containing P is also true regardless of Q.

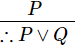
Example

• Let P be the proposition "He studies very hard."
• From P we may conclude: "Either he studies very hard or he is a very bad student." Here Q is "he is a very bad student."

Conjunction

Logical form: P, Q / ∴ P ∧ Q

Explanation: If both P and Q are known to be true, we can form the conjunction P ∧ Q. Conjunction simply combines two true statements into a single statement that is true exactly when both components are true.

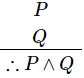
Example

• Let P be "He studies very hard."
• Let Q be "He is the best boy in the class."
• Therefore: "He studies very hard and he is the best boy in the class."

Simplification

Logical form: P ∧ Q / ∴ P (and similarly P ∧ Q / ∴ Q)

Explanation: From a conjunction one may infer either conjunct. This is truth-preserving because if P ∧ Q is true then both P and Q are individually true.

Example

• Given: "He studies very hard and he is the best boy in the class" (P ∧ Q).
• Therefore: "He studies very hard" (P).

Modus Ponens

Logical form: P, P → Q / ∴ Q

Explanation: Also called the rule of detachment. If P is true and "if P then Q" is true, then Q must be true. This rule is one of the most frequently used in proofs.

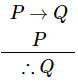
Example

• "If you have a password, then you can log on to Facebook" (P → Q).
• "You have a password" (P).
• Therefore: "You can log on to Facebook" (Q).

Modus Tollens

Logical form: P → Q, ¬Q / ∴ ¬P

Explanation: If "P implies Q" and Q is false, then P cannot be true. Modus tollens is the contrapositive form of modus ponens and is also truth-preserving.

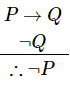
Example

• "If you have a password, then you can log on to Facebook" (P → Q).
• "You cannot log on to Facebook" (¬Q).
• Therefore: "You do not have a password" (¬P).

Disjunctive Syllogism

Logical form: P ∨ Q, ¬P / ∴ Q (or P ∨ Q, ¬Q / ∴ P)

Explanation: If we know that at least one of P or Q is true, and we know one of them is false, then the other must be true. This eliminates the false disjunct and is truth-preserving.

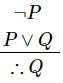
Example

• "The ice cream is not vanilla flavoured" (¬P).
• "The ice cream is either vanilla flavoured or chocolate flavoured" (P ∨ Q).
• Therefore: "The ice cream is chocolate flavoured" (Q).

Hypothetical Syllogism

Logical form: P → Q, Q → R / ∴ P → R

Explanation: If P implies Q and Q implies R, then P implies R. This rule allows chaining of conditional statements.

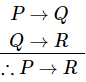
Example

• "If it rains, I shall not go to school" (P → Q).
• "If I don't go to school, I won't need to do homework" (Q → R).
• Therefore: "If it rains, I won't need to do homework" (P → R).

Constructive Dilemma

Logical form: (P → Q) ∧ (R → S), P ∨ R / ∴ Q ∨ S

Explanation: When we have two conditionals and at least one of their antecedents holds, then at least one of the consequents holds. Constructive dilemma combines a disjunction of antecedents with two implications to produce a disjunction of consequents.

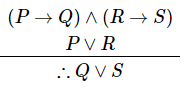
Example

• "If it rains, I will take a leave" (P → Q).
• "If it is hot outside, I will go for a shower" (R → S).
• "Either it will rain or it is hot outside" (P ∨ R).
• Therefore: "I will take a leave or I will go for a shower" (Q ∨ S).

Destructive Dilemma

Logical form: (P → Q) ∧ (R → S), ¬Q ∨ ¬S / ∴ ¬P ∨ ¬R

Explanation: If two conditionals hold and at least one of their consequents is false, then at least one of the corresponding antecedents is false. Destructive dilemma is the dual form of constructive dilemma.

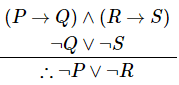
Example

• "If it rains, I will take a leave" (P → Q).
• "If it is hot outside, I will go for a shower" (R → S).
• "Either I will not take a leave or I will not go for a shower" (¬Q ∨ ¬S).
• Therefore: "Either it does not rain or it is not hot outside" (¬P ∨ ¬R).

Notes on Use and Properties

• Soundness: Each rule above is sound: whenever the premises are true, the conclusion produced by the rule is also true.
• Combining rules: Complex arguments are built by applying rules repeatedly. For example, use Conjunction to collect premises, then Modus Ponens to derive further consequences, and finally Simplification to extract components.
• Formal notation: In proofs it is common to write premises above a line and the conclusion below, or to use sequent notation: Γ ⊢ φ meaning "from the set of premises Γ we can infer φ."
• Application: Rules of inference are central to automated reasoning, program verification, formal specification, and many areas of theoretical computer science and discrete mathematics.
• Careful with informal language: Natural language examples help understanding but must be translated precisely into logical form before formal proof to avoid ambiguity.

Short Summary

Rules of inference are small, standard, truth-preserving steps used to derive conclusions from premises. Familiarity with the main rules-Addition, Conjunction, Simplification, Modus Ponens, Modus Tollens, Disjunctive Syllogism, Hypothetical Syllogism, Constructive and Destructive Dilemma-allows construction and checking of formal, valid arguments in propositional logic. These rules form the backbone of reasoning in mathematics and computer science.