Algebra of Functions | Engineering Mathematics - Engineering Mathematics PDF Download
Introduction
Algebra of functions deals with the arithmetic operations of the functions. For doing any arithmetic operation of two functions, their domains must be the same. Let us learn more about the algebra of functions along with formulas and examples.
What is Algebra of Functions?
Algebra of functions means the operations of the functions, specifically the arithmetic operations. Algebra of functions mainly deals with the following four arithmetic operations of functions:
- Addition of functions
- Subtraction of functions
- Multiplication of functions
- Division of functions
Here are the formulas of all these operations.
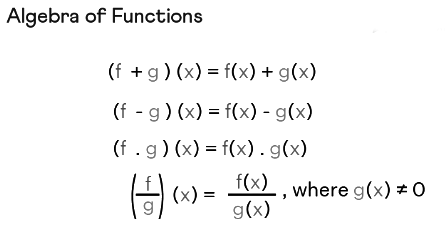
Apart from these operations, we have another two important operations composite functions and inverse functions. To learn these, you cal click on the respective links. Let us study more about these formulas and solve a few examples also using the formulas.
Algebra of Functions Formulas
Any arithmetic operation (addition/subtraction/multiplication/division) of two functions is just nothing but the same operation of independent functions. Here are the formulas for each arithmetic operation for any two functions f(x) and g(x). Note that these formulas hold only when the domains of both the functions are the same (or restricted to the same domain).
Addition of Functions
The domain of the sum of two functions is the intersection of the domain of the independent functions. The sum of two functions at a given input is equal to the sum of the independent functions at the same input. i.e.,
- (f + g) (x) = f(x) + g(x)
Example: When f(x) = x2 + 2 and g(x) = x + 1, then
(f + g)(x) = f(x) + g(x)
= x2 + 2 + x + 1
= x2 + x + 3
Since the domain of each of f(x) and g(x) is the set of all real numbers, R, the domain of (f + g)(x) (which is R ∩ R = R) is R.
Subtraction of Functions
The domain of the difference of two functions is the intersection of the domain of the independent functions. The difference of two functions at a given input is equal to the difference of the independent functions at the same input. i.e.,
- (f - g) (x) = f(x) - g(x)
Example: When f(x) = x2 + 2 and g(x) = x + 1, then
(f - g)(x) = f(x) - g(x)
= x2 + 2 - (x + 1)
= x2 - x + 1
Since the domain of each of f(x) and g(x) is the set of all real numbers, R, the domain of (f - g)(x) is R.
Multiplication of Functions
The domain of the product of two functions is the intersection of the domain of the independent functions. The product of two functions at a given input is equal to the product of the independent functions at the same input. i.e., The product of functions results in a binomial function, cubic function, or a polynomial function.
- (f · g) (x) = f(x) · g(x)
Example: When f(x) = x2 + 2 and g(x) = x + 1, then
(f · g)(x) = f(x) · g(x)
= (x2 + 2) · (x + 1)
= x3 + x2 + 2x + 2
Since the domain of each of f(x) and g(x) is the set of all real numbers, R, the domain of (f · g)(x) is R.
Division of Functions
The domain of the quotient of two functions is the intersection of the domain of the independent functions. But we have to take care of the extra condition, setting the denominator function to "not equal to 0" because if the denominator is 0, then the fraction is undefined. The quotient of two functions at a given input is equal to the quotient of the independent functions at the same input. i.e.,
- (f / g) (x) = f(x) / g(x), given g(x) ≠ 0
Example: When f(x) = x2 + 2 and g(x) = x + 1, then
(f / g)(x) = f(x) / g(x)
= (x2 + 2) / (x + 1)
Since the domain of each of f(x) is the set of all real numbers, R; and the domain of g(x) is the set of all real numbers except -1 (as x + 1 is in the denominator, x + 1 ≠ 0 ⇒ x ≠ -1). So the domain of (f / g)(x) is R - {-1}.
Important Notes on Algebra of Functions:
For any two functions f(x) and g(x):
- (f + g) (x) = f(x) + g(x)
- (f - g) (x) = f(x) - g(x)
- (f · g) (x) = f(x) · g(x)
- (f / g) (x) = f(x) / g(x), g(x) ≠ 0
|
65 videos|129 docs|94 tests
|
















