Laws of Boolen Algebra | Digital Logic - Computer Science Engineering (CSE) PDF Download
| Table of contents |

|
| Introduction |

|
| Truth Tables: |

|
| Description of the Laws of Boolean Algebra |

|
| Boolean Postulates – |

|
| Boolean Algebra Functions |

|
| Example |

|
Introduction
A set of rules or Laws of Boolean Algebra expressions have been invented to help reduce the number of logic gates needed to perform a particular logic operation resulting in a list of functions or theorems known commonly as the Laws of Boolean Algebra.

As well as the logic symbols “0” and “1” being used to represent a digital input or output, we can also use them as constants for a permanently “Open” or “Closed” circuit or contact respectively.
Boolean Algebra is the mathematics we use to analyze digital gates and circuits. We can use these “Laws of Boolean” to both reduce and simplify a complex Boolean expression in an attempt to reduce the number of logic gates required. Boolean Algebra is therefore a system of mathematics based on logic that has its own set of rules or laws, which are used to define and reduce Boolean expressions.
The variables used in Boolean Algebra only have one of two possible values, a logic “0” and a logic “1” but an expression can have an infinite number of variables all labelled individually to represent inputs to the expression, For example, variables A, B, C etc., giving us a logical expression of A + B = C, but each variable can ONLY be a 0 or a 1.
Examples of these individual laws of Boolean, rules and theorems for Boolean Algebra are given in the following table.
Truth Tables:
A truth table is a simple and useful tool used in Boolean algebra to show how a logical expression behaves for all possible combinations of input values. It lists all the possible input values (usually as 0s and 1s) and shows the corresponding output for each case. The following are the truth tables for NOT, AND, OR, and XOR operations.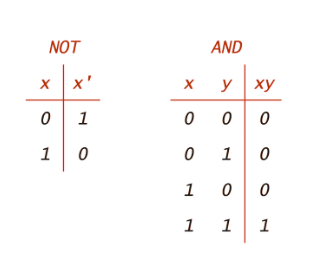

The fundamental laws of Boolean algebra — namely the commutative law (which allows the rearrangement of terms in addition and multiplication), the associative law (which allows the removal or regrouping of brackets), and the distributive law (which allows expressions to be factored) — function similarly to those in regular algebra.
Although these laws are often shown using one or two variables, they are not limited to that. They can be applied to expressions with any number of variables. These Boolean laws are essential tools for proving Boolean expressions and simplifying complex digital circuits.
Below is a brief overview of the different Boolean laws, where A represents a variable input.
Description of the Laws of Boolean Algebra
1. Annulment Law –
A term AND‘ed with a “0” equals 0 or OR‘ed with a “1” will equal 1
- A . 0 = 0 - A variable AND’ed with 0 is always equal to 0
- A + 1 = 1 - A variable OR’ed with 1 is always equal to 1
2. Identity Law –
A term OR‘ed with a “0” or AND‘ed with a “1” will always equal that term
- A + 0 = A - A variable OR’ed with 0 is always equal to the variable
- A . 1 = A - A variable AND’ed with 1 is always equal to the variable
3. Idempotent Law –
An input that is AND‘ed or OR´ed with itself is equal to that input
- A + A = A - A variable OR’ed with itself is always equal to the variable
- A . A = A - A variable AND’ed with itself is always equal to the variable
4. Complement Law –
A term AND‘ed with its complement equals “0” and a term OR´ed with its complement equals “1”
- A . A' = 0 - A variable AND’ed with its complement is always equal to 0
- A + A' = 1 - A variable OR’ed with its complement is always equal to 1
5. Commutative Law –
The order of application of two separate terms is not important
- A . B = B . A - The order in which two variables are AND’ed makes no difference
- A + B = B + A - The order in which two variables are OR’ed makes no difference
6. Double Negation Law –
A term that is inverted twice is equal to the original term
( A' )' = A - A double complement of a variable is always equal to the variable
7. De Morgan’s Theorem –
There are two “de Morgan’s” rules or theorems,
(1) Two separate terms NOR‘ed together is the same as the two terms inverted (Complement) and AND‘ed for example: 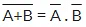
(2) Two separate terms NAND‘ed together is the same as the two terms inverted (Complement) and OR‘ed for example: 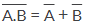
Other algebraic Laws of Boolean not detailed above include:
Boolean Postulates –
While not Boolean Laws in their own right, these are a set of Mathematical Laws which can be used in the simplification of Boolean Expressions.
- 0 . 0 = 0 A 0 AND’ed with itself is always equal to 0
- 1 . 1 = 1 A 1 AND’ed with itself is always equal to 1
- 1 . 0 = 0 A 1 AND’ed with a 0 is equal to 0
- 0 + 0 = 0 A 0 OR’ed with itself is always equal to 0
- 1 + 1 = 1 A 1 OR’ed with itself is always equal to 1
- 1 + 0 = 1 A 1 OR’ed with a 0 is equal to 1
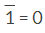 The Inverse (Complement) of a 1 is always equal to 0
The Inverse (Complement) of a 1 is always equal to 0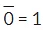 The Inverse (Complement) of a 0 is always equal to 1
The Inverse (Complement) of a 0 is always equal to 1
1. Distributive Law –
This law permits the multiplying or factoring out of an expression.
- A(B + C) = A.B + A.C (OR Distributive Law)
- A + (B.C) = (A + B).(A + C) (AND Distributive Law)
2. Absorptive Law –
This law enables a reduction in a complicated expression to a simpler one by absorbing like terms.
- A + (A.B) = (A.1) + (A.B) = A(1 + B) = A (OR Absorption Law)
- A(A + B) = (A + 0).(A + B) = A + (0.B) = A (AND Absorption Law)
3. Associative Law –
This law allows the removal of brackets from an expression and regrouping of the variables.
- A + (B + C) = (A + B) + C = A + B + C (OR Associate Law)
- A(B.C) = (A.B)C = A . B . C (AND Associate Law)
Boolean Algebra Functions
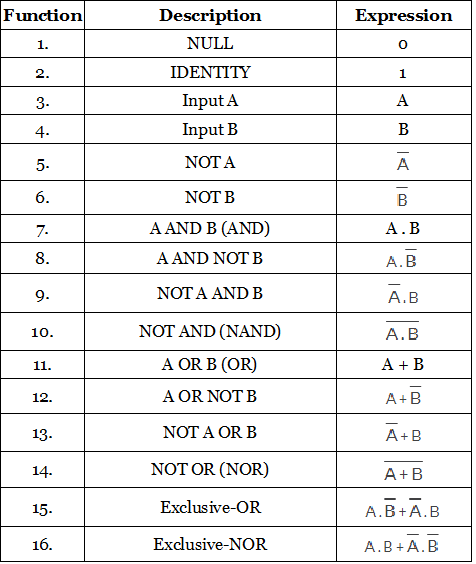
Using the information above, simple 2-input AND, OR and NOT Gates can be represented by 16 possible functions as shown in the following table.
Example
Using the above laws, simplify the following expression: Q = (A + B)(A + C)

Then the expression: (A + B)(A + C) can be simplified to A + (B.C) as in the Distributive law.
|
53 docs|15 tests
|
FAQs on Laws of Boolen Algebra - Digital Logic - Computer Science Engineering (CSE)
| 1. What are truth tables and how are they used in Boolean algebra? |  |
| 2. What are the basic laws of Boolean algebra? |  |
| 3. Can you explain the concept of Boolean postulates? |  |
| 4. How can Boolean algebra functions be simplified? |  |
| 5. What is the significance of Boolean algebra in computer science engineering? |  |















