Arithmetic Circuits - 2 | Digital Logic - Computer Science Engineering (CSE) PDF Download

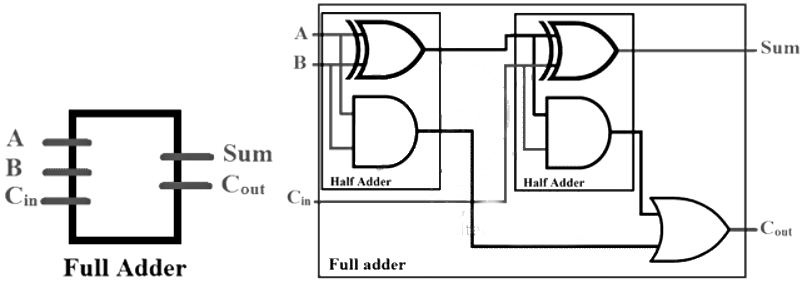
What is Ripple Carry Adder?

• Ripple carry adder as the name suggest is an adder in which the carry bit ripple through all the stages of the adder.
• The ripple carry adder contain individual single bit full adders which consist of 3 inputs (Augend, Addend and carry in) and 2 outputs (Sum, carry out). These full adders are connected together in cascade form to create a ripple carry adder.

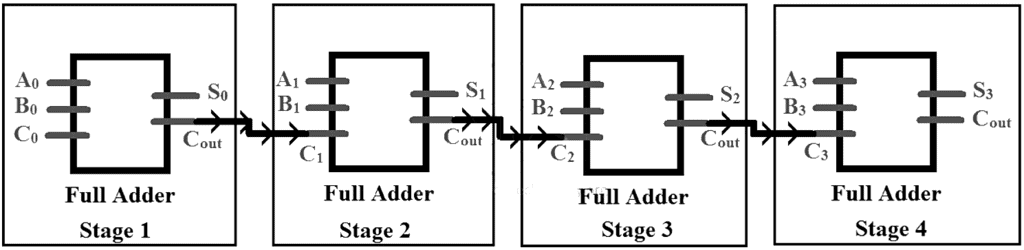
• ‘n’ full adders combine together to form ‘n’ bit adder.
• ‘n’ bit adder will have ‘n’ stages and each stage’s output will depend upon previous stage’s carry out.
• Each stage can calculate the sum at the same time based on the input numbers but the sum will not be valid because the carry in to each of these stages will not be available yet.
• For example in a 4-bit adder, there are 4 stages for each bit addition. The stage 1 being the LSB bit will first evaluate Sum, C_out and pass C_out to 2nd stage as C_in.
• Then the 2nd stage will evaluate C_out ­and pass it to 3rd stage for calculation and then the 3rd stage will pass it forward to the 4th stage and now the 4th stage can evaluate the Sum and C_out. Now the sum we will get will be a valid output.
  
• In 4 bit adder, the time delay for a valid output is the sum of time delay of 4 full adders, if there is an ‘n’ bit adder, than the time delay will be the sum of time delay of ‘n’ full adders. It means, higher the bit size of the numbers, the late the answer we will get. So it is not an efficient design for complex and fast working systems.
• The addition could be done as soon as the input numbers (Augend and addend) were provide to the adder but because of the carry propagation, the adder is not able to provide a valid answer until it reaches the last stage.
• The time that the carry took to propagate from the first adder to the last adder is known as propagation delay. The major drawback of Ripple carry adder is this Propagation delay. But the design of Ripple carry adder is very simple and inexpensive.

What is Carry Look Ahead Adder (CLA)

• As we have discussed in the ripple carry adder that the adder takes a time delay to compute sum because the carry was propagated through all the gates from input to output. To increase the speed of the addition we need to provide the carry bits used by these adders without the wait for the preceding additions.
• So that the addition of all bits is done at the same time.The idea used to compute the carry bits before the addition is known as Carry look ahead logic.
• Carry look ahead is a digital circuit used for determining the carry bits used by the adder for addition without the wait for the carry propagation. It generates the carry bits for all the stages of the addition at the same time as soon as the input signal (Augend, addend, carry in) is provided.
• Due to this technique the adders don’t have to wait for the carry propagation and a valid sum is computed without any delay.

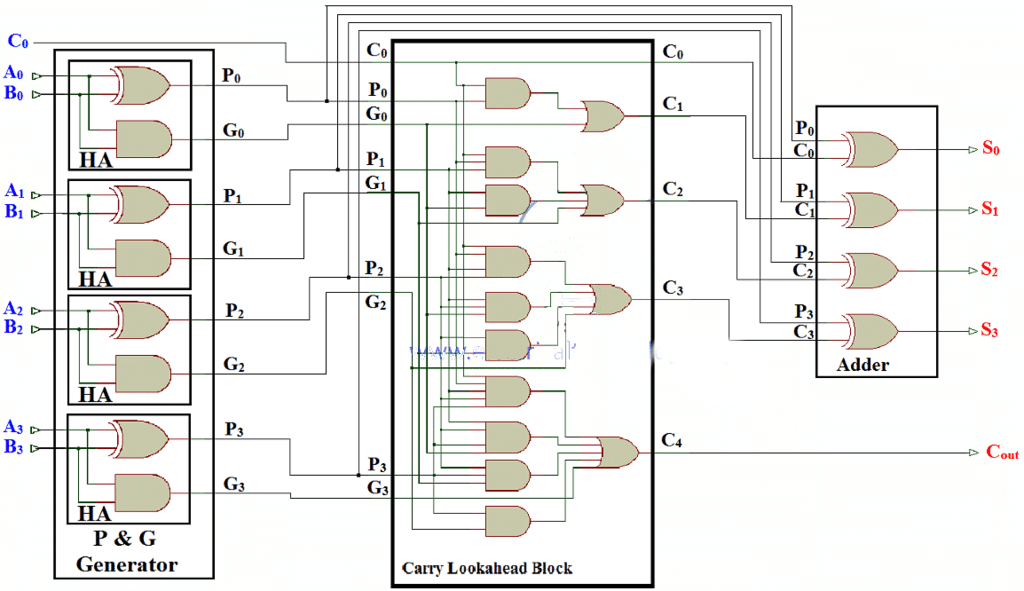
Carry Look Ahead Adder (CLA) Logic Diagram

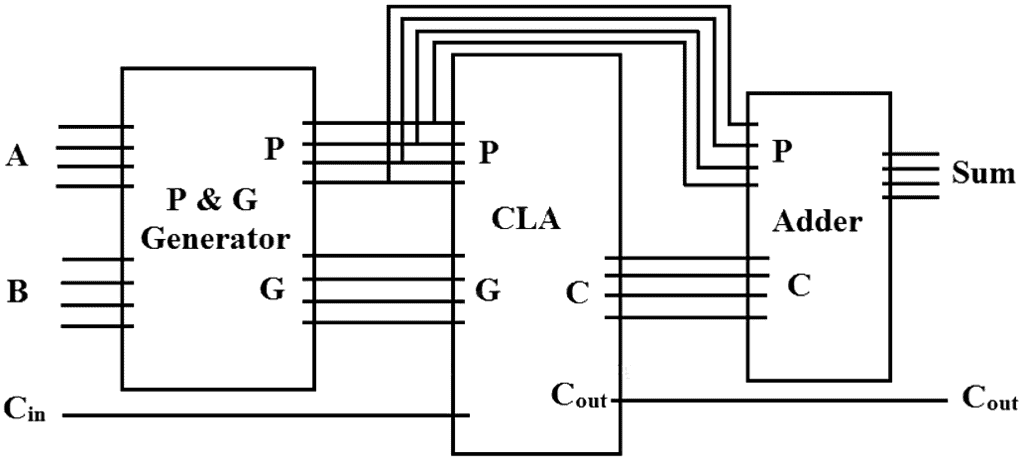
• Carry look ahead adder’s (CLA) logic diagram is given below. It contains 3 blocks; “P and G generator”, “Carrylook ahead” block and “adder block”. Input “Augend”, “Addend” is provided to the “P and G generator” block whose output is connected with CLA and the adder block.
• CLA block produces carry bits C₁, C₂, C₃, C₄ and provide it to the adder block and evaluate sum S₀, S₁, S₂,  S₃, based on these inputs. C₄ is taken as Cout.

Carry look ahead Adder (CLA) logic diagramFig 3- Carry look ahead Adder (CLA) logic diagram

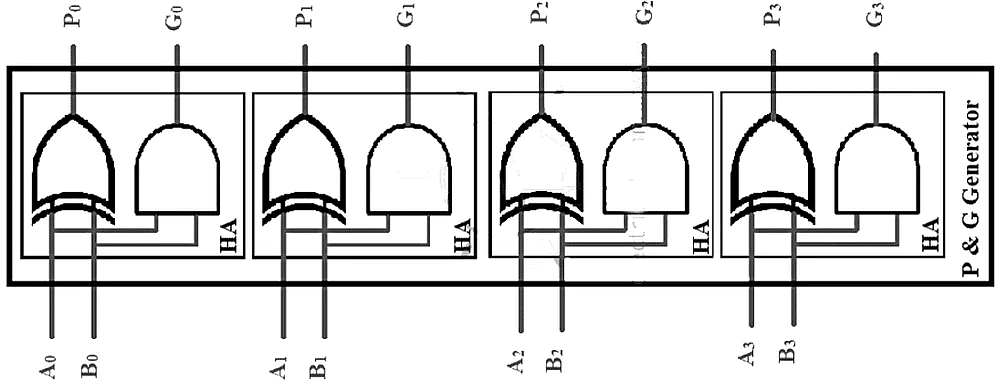
P and G Generator: Half Adder

• This block consists of half adders used for generating P and G terms of each bit.
• This block generate these terms needed for the CLA because the carry depends on it.
  Carry =    AB + C_in (A XOR B)
• P = (A XOR B): P is known as Carry propagate, because it propagates the Cin from previous stage to the next stage.
• G = AB:  G is known as Carry Generate, because it can directly generate carry bit without any Cin.
• P and G terms for a 4 bit number will be:
  P₀ = (A₀ XOR B₀), G₀ = A₀B₀ ,
  P₁ = (A₁ XOR B₁), G₁ = A₁B₁ ,
  P₂ = (A₂ XOR B₂), G₂ = A₂B₂ ,
  P₃ = (A₃ XOR B₃), G₃ = A₃B₃ ,
• These P and G terms will be later used by CLA block.

Carry Lookahead (CLA) Block Diagram

• CLA block contains combinational circuit used to determine the carry bits. it takes Augend, Addend and carry in as inputs and produce the carry bits.
• Consider A, B two numbers being added both 4 bits wide and C0 as carry in. And C₁, C₂, C₃, C₄ are the output carry bits.
• First we will derive C₁, C₂, C₃, C₄ using the carry equation from full adder.
  Carry = AB + Cin (A XOR B)
  P  =  (A XOR B)
  G = AB ,
  Carry =  G + Cin P
• So C₁, C₂, C₃, C₄ will become:
  C₁  = G₀ + C₀P₀
  C₂ = G₁ + C₁P₁  = G₁ + (G₀ + C₀P₀)P₁  =  G₁ + G₀ P₁+ C₀P₀P₁
  C₃ = G₂ + C₂P₂  =  G₂ + (G₁ + G₀ P₁ + C₀P₀P₁)P₂  =  G₂ + G₁P₂ + G₀ P₁P₂ + C₀P₀P₁P₂
  C₄ = G₃  + C₃P₃ = G₃ + (G₂ + G₁P₂ + G₀ P₁P₂ + C₀P₀P₁P₂)P₃ = G₃ + G₂ P₃ + G₁P₂ P₃ + G₀ P₁P₂P₃ + C₀P₀P₁P₂P₃
• Thus it shows that none of these carry bits depend on their previous stage carry bits. They only need A , B and C₀.

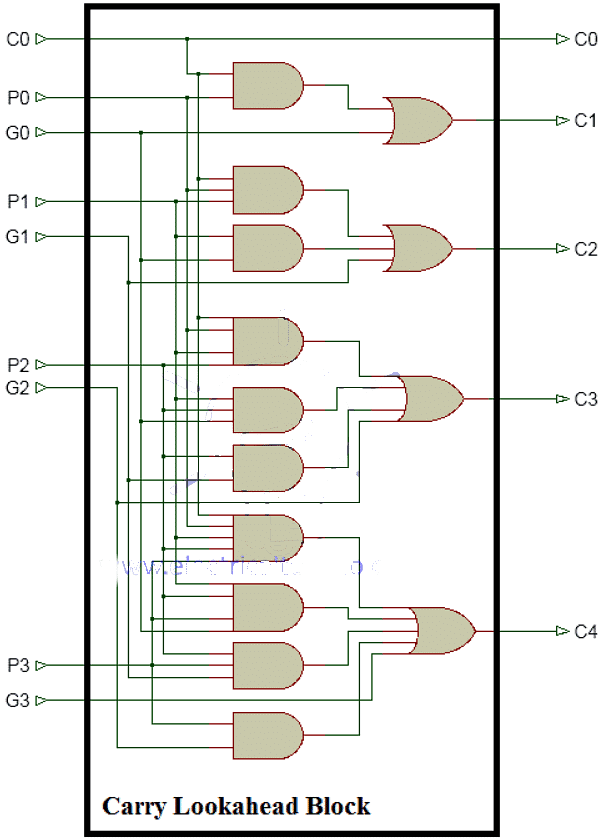
• This carry look ahead block will generate these carry bits and provide it to the adders block for addition.

Adders Block

• As we know that the carry bits will be provided by the CLA block so we don’t need Full adders to evaluate the carry bits. We only need the sum which is:
  S = C_inXOR (A XOR B)
• So the sum of each bit will be
  S₀ = C₀ XOR (A₀ XOR B₀) = C₀ XOR (P₀)
  S₁­ = C₁ XOR (A₁ XOR B₁) = C₁ XOR (P₁)
  S₂ = C₂ XOR (A₂ XOR B₂) = C₂ XOR (P₂)
  S₃­ = C₃ XOR (A₃ XOR B₃) = C₃ XOR (P₃)
• And the last carry C₄ will be the C_out­ of the CLA full adder.
  C_out  = C₄

Full Schematic of Carry look ahead adder is given in figure below.

4-BIT Look-Ahead Carry Generator – 74182 TTL IC Details

• 74182  TTL is Carry generator working on Carry look ahead logic.

Inputs:  P̅₀ = invert of P₀, G̅₀ = invert of G₀ 
Outputs: C_n = C₀, G̅= COUT

P̅1= invert of P₁, G̅₁ = invert of G₁ C_n+x  = C₁, P̅=P̅₀P̅₁P̅₂P̅₃
P̅2= invert of P₂ , G̅₂ = invert of G₂ C_n+y = C₂
P̅3= invert of P₃ ,G̅₃ = invert of G₃ C_n+z = C₃