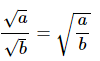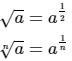What do you mean by surds? | Mathematics for Grade 10 PDF Download
| Table of contents |

|
| Surds |

|
| What Do You Mean by Surds? |

|
| What Are the Rules of Surds? |

|
| Simplify Surd Calculation with Steps |

|
| Solved Examples |

|
Surds
The Latin meaning of the word "Surd" is deaf or mute. In earlier days, Arabian mathematicians called rational numbers and irrational numbers as audible and inaudible. Since surds form are made of irrational numbers, they were referred to as asamm (deaf, dumb) in Arabic language, and were later translated in Latin as surds. With this awareness, let's move ahead to learn the working of surds in math.
With this awareness, let's move ahead to learn the working of surds in math.
In this mini-lesson, we shall explore the topic of surds, by finding answers to questions like what do you mean by surds, what are the rules of surds, and simplifying calculations with surds.
What Do You Mean by Surds?
Surd is simply used to refer to a number that does not have a root.
√4 , ∛ 8 , √25 have roots as answers.
But √6 , ∛2 , √20 do not have proper roots.
These number forms are termed as surds.
Also, these surds example expressed in exponential form would have fractions as powers.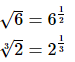
According to surds definition, there are three different types of surds.
Pure Surds: A surd having only a single irrational number is called a pure surd.
√7 , ∜11 , √x3
Mixed Surds: A surd having a mix of a rational number and an irrational number is called a mixed surd.
x√y , 4√3 , 8√5
Compound Surds: A surd composed of two surds is called a compound surd.
4 + √3 , √5 + √2 , , √a + b√c
What Are the Rules of Surds?
A few rules of working with surds are:
- Surds cannot be added.
√a + √b ≠ √(a + b) - Surds cannot be subtracted.
√a − √b ≠ √(a − b) - Surds can be multiplied.
√a × √b = √(a × b) - Surds can be divided.

- Surds can be written in exponential form.

Tips:
Generally, surds cannot be added. But we can add similar surds.
m√a + n√a = (m + n)√a
3√5 + 2√5 = 5√5
Now try to find the solution for the following surds.
2√5+√3+√2+√5+2√3=?
Simplify Surd Calculation with Steps
Simplification of surds is needed for performing calculations.
There are two simple steps to surd simplification.
STEP - 1: Split the number within the root into its prime factors.
STEP-II: Based on the root write the prime factors, outside the root. In case of square root, write one factor outside the root, for every two similar factors within the root.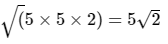
Example: Let us use the above steps to perform the following calculation.
√18 + √50
The above operation of addition is not possible without further simplification.
√18+√50=√(3×3×2)+√(5×5×2)
=3√2+5√2
=8√2
Solved Examples
Example 1: Convert √80 into mixed surd.
√80 =√(16×5)
= √(2×2×2×2×5)
= 2×2×√5
= 4√5
∴√80 = 4√5
Example 2: Find the product of 4√3 and 2√5
4√3×2√5= 4×2×√3×√5
= 8×√(3×5)
= 8√15
∴ The product is 8√15
Example 3: Write the expansion of (4 + 3 √2)2
(4 + 3√2)2 = 42 + (3√2)2 + 2.4.3√2
= 16 + 18 + 24√2
= 34 + 24√2
∴ The result of expansion is 34 + 24√2
Example 4: Find the sum of (2√5 − 4√2) , (3√5 + 5√2)
(2√5 − 4√2) + (3√5 + 5√2) = 2√5 − 4√2 + 3√5 + 5√2
= 5√2 – 4√2 + 2√5 + 3√5
= √ 2 + 5 √5
∴ The sum is √ 2 + 5 √ 5
Example 5: Find the product of the surds (√2 + 5√3) , (√3 – 2√5)
(√2 + 5√3) × (√3 – 2√5) = √2 (√3 – 2√5) + 5√3 (√3 – 2√5)
= √2 × √3 − √2 × 2√5 + 5√3 × √3 − 5√3 × 2√5
= √6 − 2√10 − 5√9 − 10√15
= − 5 × 3 + √6 − 2 √10 − 10√15
= − 15 + √6 − 2√10 − 10√15
∴ The product is − 15 + √6 − 2√10 − 10√15
|
138 videos|67 docs|41 tests
|

|
Explore Courses for Grade 10 exam
|

|