What are Indices? | Mathematics for Grade 10 PDF Download
| Table of contents |

|
| Indices |

|
| What are Indices? |

|
| Properties of Indices |

|
| Negative Indices |

|
| Indices with Fractions |

|
| Decimal Indices |

|
| Scientific Notation with Indices |

|
Indices
An indices of a number shows how many times we are multiplying a number by itself. For example, 34 means we are multiplying 3 four times. Its expanded form is 3 × 3 × 3 × 3. Indices is also known as the power of a number. It can be a whole number, fraction, negative number, or decimals. Let's learn more about indices in this article.
What are Indices?
The indices of a number shows how many times the number is multiplied by itself. For example, 2×2×2×2 can be written as 24, as 2 is multiplied by itself 4 times. Here, 2 is called the "base" and 4 is called the "indices" or "power." In general, xn means that x is multiplied by itself for n times.
indices of a Number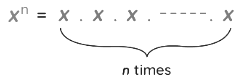
Here, in the term xn,
- x is called the "base"
- n is called the "indices"
- xn is read as "x to the power of n" (or) "x raised to n".
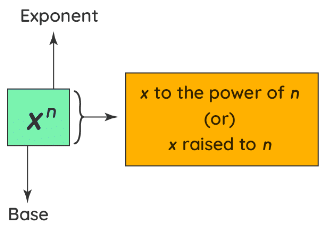
Some examples of indices are as follows:
- 3 × 3 × 3 × 3 × 3 = 35
- -2 × -2 × -2 = (-2)3
- a × a × a × a × a × a = a6
indices are important because, without them, when a number is repeated by itself many times it is very difficult to write the product. For example, it is very easy to write 57 instead of writing 5 × 5 × 5 × 5 × 5 × 5 × 5.
Properties of Indices
The properties of indices or laws of indices are used to solve problems involving indices. These properties are also considered as major indices rules to be followed while solving indices. The properties of indices are mentioned below.
- Law of Product: am × an = am+n
- Law of Quotient: am/an = am-n
- Law of Zero indices: a0 = 1
- Law of Negative indices: a-m = 1/am
- Law of Power of a Power: (am)n = amn
- Law of Power of a Product: (ab)m = ambm
- Law of Power of a Quotient: (a/b)m = am/bm
Negative Indices
A negative indices tells us how many times we have to multiply the reciprocal of the base. For example, if it is given that a-n, it can be expanded as 1/an. It means we have to multiply the reciprocal of a, i.e 1/a 'n' times. Negative indices are used while writing fractions with indices. Some of the examples of negative indices are 2 × 3-9, 7-3, 67-5, etc. We can convert these into positive indicesas follows:
- 2 × 3-9 = 2 × (1/39) = 2/39
- 7-3 = 1/73
- 67-5 = 1/675
Indices with Fractions
If an indices of a number is a fraction, it is known as a fractional indices. Square roots, cube roots, nth root are parts of fractional indices. Number with power 1/2 is termed as the square root of the base. Similarly, a number with a power of 1/3 is called the cube root of the base. Some examples of indices with fractions are 52/3, -81/3, 105/6, etc. We can write these as:
- 52/3 = (52)1/3 = 251/3 = ∛25
- -81/3 = ((-2)3)1/3 = -2
- 105/6 = (105)6 = 6√105 = 6√100000
Decimal Indices
If an indices of a number is given in the decimal form, it is known as a decimal indices. It is slightly difficult to evaluate the correct answer of any decimal indices so we find the approximate answer for such cases. Decimal indices can be solved by first converting the decimal in fraction form. For example, 41.5 can be written as 43/2 which can be simplified further to get the final answer 8. i.e., 43/2 = (22)3/2 = 23 = 8.
Scientific Notation with Indices
Scientific notation is the standard form of writing very large numbers or very small numbers. In this, numbers are written with the help of decimal and powers of 10. A number is said to be written in scientific notation when a number between 0 to 10 is multiplied by a power of 10. In the case of a number greater than 1, the power of 10 will be a positive indices, while in the case of numbers less than 1, the power of 10 will be negative. Let's understand the steps for writing numbers in scientific notation with indices:
- Step 1: Put a decimal point after the first digit of the number from the left. If there is only one digit in a number excluding zeros, then we don't need to put decimal.
- Step 2: Multiply that number with a power of 10 such that the power will be equal to the number of times we shift the decimal point.
By following these two simple steps we can write any number in standard form with indices, for example, 560000 = 5.6 × 105, 0.00736567 = 7.36567 × 10-3.
|
137 videos|83 docs|44 tests
|




















