Cosine Rule | Mathematics for Grade 10 PDF Download
| Table of contents |

|
| Law of Cosines |

|
| What is Law of Cosines? |

|
| Law of Cosines: Definition |

|
| Law of Cosines Formula |

|
| Proof of Law of Cosines |

|
| Finding Missing Length and Angles Using the Law of Cosines |

|
Law of Cosines
The law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. Using trigonometry, we can now obtain values of distances and angles which cannot be measured otherwise. The law of cosines finds application while computing the third side of a triangle given two sides and their enclosed angle, and for computing the angles of a triangle if all three sides are known to us.
A triangle has 6 elements (3 sides + 3 angles). Let us understand the law of the cosines formula and its derivation to study the inter-relationship of these elements using the cosine function.
What is Law of Cosines?
The law of cosine helps in establishing a relationship between the lengths of sides of a triangle and the cosine of its angles. The cosine law in trigonometry generalizes the Pythagoras theorem, which applies to a right triangle.
Law of Cosines: Definition
Statement: The law of cosine states that the square of any one side of a triangle is equal to the difference between the sum of squares of the other two sides and double the product of other sides and cosine angle included between them.
Let a, b, and c be the lengths of the three sides of a triangle and A, B, and C be the three angles of the triangle. Then, the law of cosine states that: a2 = b2 + c2 − 2bc·cosA. As stated above, the law of cosines in trigonometry generalizes the Pythagorean theorem. If you plug 90º for the angle in one of the rules, what will happen? Since cos 90º = 0, we are left with the Pythagoras theorem. The law of cosine is also known as the cosine rule. This law is useful to find the missing information in any triangle. For example, if you know the lengths of two sides of a triangle and an angle included between them, this rule helps to find the third side of the triangle. Let us check out different cosine law formulas and the method to find these missing parameters in the following sections.
The law of cosine is also known as the cosine rule. This law is useful to find the missing information in any triangle. For example, if you know the lengths of two sides of a triangle and an angle included between them, this rule helps to find the third side of the triangle. Let us check out different cosine law formulas and the method to find these missing parameters in the following sections.
Law of Cosines Formula
The law of cosines formula can be used to find the missing side of a triangle when its two sides and the included angle is given i.e., it is used in the case of a SAS triangle. We know that if A, B, and C are the vertices of a triangle, then their opposite sides are represented by the small letters a, b, and c respectively. The law of cosines formula is used to:
- find a when b, c, and A are given (or)
- find b when a, c, and B are given (or)
- find c when a, b, and C are given (or)
- find any angle of the triangle when a, b, and c are given.
There are three laws of cosines and we choose one of them to solve our problems depending on the available data.
a2 = b2 + c2 - 2bc·cosA
b2 = c2 + a2 - 2ca·cosB
c2 = a2 + b2 - 2ab·cosC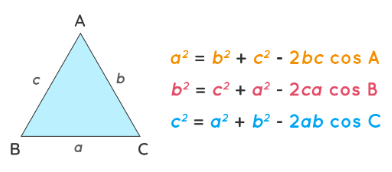
Proof of Law of Cosines
There is more than one way to prove the law of cosine. Let's prove it using trigonometry. Consider the following figure.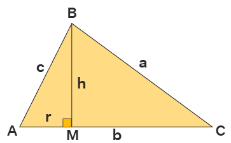
In ΔABM we have,
sin A = BM/AB = h/c
and,
cos A = AM/AB = r/c
From equation (1) and (2), we get h = c(sin A) and r = c(cos A)
By Pythagoras Theorem in ΔBMC,
a2 = h2 + (b - r)2
Substitute h = c(sin A) and r = c(cos A) in equation (3).
a2 = (c(sinA))2 + (b - c(cosA))2
= c2sin2A + b2 + c2cos2A - 2bc·cosA
= c2(sin2A + cos2A) + b2 - 2bc·cosA
= c2 + b2 - 2bc·cosA
Hence, proved.
Finding Missing Length and Angles Using the Law of Cosines
As discussed above, law of cosines can be used to calculate the missing parameters of a triangle, given the required known elements. Let us have a look at the following steps to understand the process of finding the missing side or angle of a triangle using the cosine law.
- Step 1: Note down the given data(side lengths and measure of angles) for the triangle and identify the element to be calculated.
- Step 2: Apply the cosine rule formulas,
a2 = b2 + c2 - 2bc·cosA
b2 = c2 + a2 - 2ca·cosB
c2 = a2 + b2 - 2ab·cosC
where, A, B, and C are the vertices of a triangle, and their opposite sides are represented as a, b, and c respectively. - Step 3: Express the obtained result with suitable units.
Let us consider a few examples to find the missing side and angle of a triangle.
Example 1: Look at the figure shown below.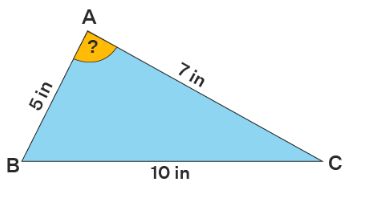
We need to find the measure of ∠A.
We will use the formula
a2 = b2 + c2 - 2bc.cosA. Substitute 10 for 'a', 7 for 'b' and 5 for 'c'.
102 = (7)2 + (5)2 - 2(5)(7)·cosA
70·cos A = -26
cos A = -13/35
A = 111.8º
In this example, we used the law of the cosine equation to find the missing angle. Now, let us use the law of the cosine equation to find the missing side.
Example 2: Two sides of a triangle measure 72 in and 50 in with the angle between them measuring 49º let us find the missing side.
Substitute 72 for b, 50 for c and 49º for A.
Using the law of cosines formula,
a2 = b2 + c2 - 2bc·cosA
a2 = (72)2 + (50)2 - 2(72)(50)cos49º
a2 = 5184 + 2500 - (7200)(0.656)
a2 = 5184 + 2500 - 4723.2
a2 = 2960.8
a ≈ 54.4
So, the missing length of the side is 54.4 inches.
Important Notes on Law of Cosines:
- Three different versions of the law of cosine are:
a2 = b2 + c2 - 2bc·cosA
b2 = c2 + a2 - 2ca·cosB
c2 = a2 + b2 - 2ab·cosC - Pythagoras Theorem is a generalization of the Law of Cosine.
- The law of cosine can be applied in any triangle.
Solved Example
Example 1: A boy is standing at point A and two boats are located at points, B and C, such that the positions of all three form a triangle. If the measure of angle A is 36º with the lengths AB and AC measuring 2.5 ft and 1.8 ft respectively, determine the distance between the two boats floating at the lake.
The law of cosine is expressed in three different ways.
We will use the formula a2 = b2 + c2 - 2bc·cos A, because the required side is opposite to ∠A.
Substitute 1.8 for 'b', 2.5 for 'c' and 36º for angle A.
a2 = b2 + c2 - 2bc·cosA
a2 = (1.8)2 + (2.5)2 - 2(1.8)(2.5)cos 36º
a2 = 3.24 + 6.25 - (9)(0.8)
a2 = 3.24 + 6.25 - 7.2
a2 = 2.29
a ≈ 1.5
The length across the boats is 1.5 feet.
Example 2: A farmer has a huge field in the shape of a triangle. The two sides of the field measure 624 ft and 327 ft and the angle between them measures 93º. Calculate how much fencing is needed to enclose the field?
We will use the definition of law of cosine: a2 = b2 + c2 - 2bc·cosA.
Substitute 624 for 'b', 327 for 'c' and 93º for A.
a2 = b2 + c2 - 2bc·cosA
a2 = (624)2 + (327)2 - 2(624)(327)cos 93º
a2 = 389376 + 106929 - (408096)(-0.05)
a2 = 389376 + 106929 + 20404.8
a2 = 516709.8
a ≈ 719
So, the perimeter of the triangular field is 624 + 327 + 719 = 1670ft
The farmer will need 1670 ft of fencing.
Example 3: The adjacent sides of a parallelogram measure 6 in and 10 in with the angle between them measuring 79º. Can you determine the length of the diagonal of the parallelogram?
Given: Let ABCD be a parallelogram, such that, CD = 6 in, BC = 10 in.
We know that the adjacent angles of a parallelogram are supplementary.
So, ∠B = 180º - ∠C = 180º - 79º = 101º.
Also, the opposite sides of a parallelogram are equal.
So, AB = CD = 6 in.
Let's apply the cosine rule in ΔABC.
Substitute 10 for 'a', 6 for 'c' and 101º for B.
b2 = a2 + c2 - 2ac·cosB
b2 = (10)2 + (6)2 - 2(10)(6)cos101º
b2 = 100 + 36 - (120)(-0.19)
b2 = 100 + 36 + 22.8
b2 = 158.8
b ≈ 12.6
The length of the diagonal is approximately 12.6 inches.
|
138 videos|67 docs|41 tests
|

|
Explore Courses for Grade 10 exam
|

|
















