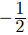Class 10 Maths Chapter 10 Assertion and Reason Questions - Circles

Directions: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:

Question 1:
Assertion (A) : In the given figure, O is the centre of a circle and AT is a tangents at point A, then ∠BAT = 60º.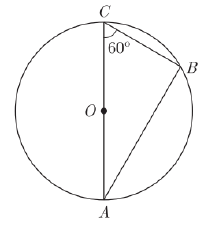 

Reason (R) : A straight line can meet a circle at one point only.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.

Correct Answer is Option (c)
We have, ∠ ABC = 90°
(Angle in the semi-circle)
In Δ ABC
∠ ABC + ∠ACB+ ∠ CAB = 180°
(Angle sum property of A ABC)
⇒ 90° + 60° + ∠ CAB = 180°
⇒  ∠CAB — 30°
Now,    OA ⊥ A T
∠BAT = 90° -30" =60°
So, A is correct but R is incorrect.

Question 2: 
Assertion (A) : If length of a tangent from an external point to a circle is 8 cm, then length of the other tangent from the same point is 8 cm.
Reason (R) : Length of the tangents drawn from an external point to a circle are equal.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.

Correct Answer is Option (a)

Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).

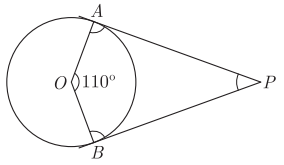
Question 3: Assertion (A) : PA and PB are two tangents to a circle with centre O. Such that ∠AOB = 110°, then +APB = 90°.
Reason (R) : The length of two tangents drawn from an external point are equal.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.

Correct Answer is Option (d)
We have, OA ⊥ AP
and OB ⊥ PB
In quadrilateral, OAPB , we have
∠OAP + ∠APB + ∠PBO + ∠AOB = 360°
90° + ∠APB + 90° + 110° = 360°
∠APB = 70°
(Radius is perpendicular to the tangent at point of tangency)

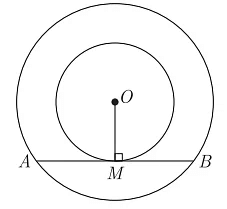
Question 4: Assertion (A) : In the given figure, a quadrilateral ABCD is drawn to circumscribe a given circle, as shown. Then AB + BC = AD + DC.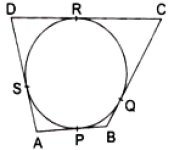

Reason (R) : In two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.

Correct Answer is Option (d)

We have two concentric circles O is the centre of concentric circles and AB is the tangent
OM ⊥ AB
AM = MB
(Perpendicular from centre O to the chord AB bisect the chord AB )
So, A is incorrect but R is correct. Hence, (d) is the correct option.

Question 5: Assertion (A) : If in a cyclic quadrilateral, one angel is 40° , then the opposite angle is 140°. 
Reason (R) : Sum of opposite angles in a cyclic quadrilateral is equal to 360°.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.

Correct Answer is Option (c)

Angle + 400 = 1800
Angle = 1800 - 400 = 1400

Question 6:  Assertion (A) : The two tangents are drown to a circle from an external point, than they subtend equal angles at the centre.
Reason (R) : A parallelogram circumscribing a circle is a rhombus.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.

Correct Answer is Option (b)

From an external point the two tangents drawn subtend equal angles at the centre. So A is true. Also, a parallelogram circumscribing a circle is a rhombus, so R is also true but R is not correct explanation of A.

Question 7: 
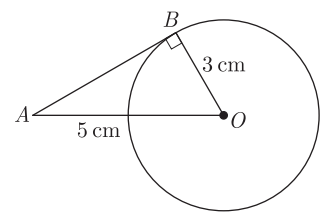
Assertion (A) : If in a circle, the radius of the circle is 3 cm and distance of a point from the centre of a circle is 5 cm, then length of the tangent will be 4 cm.
Reason (R) : (hypotenuse) ² = (base) ² + (height) ²
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.

Correct Answer is Option (a)

(OA)² = (AB)²+(OB)²

 (AB) = = 4 cm

Question 8: Assertion (A) : Centre and radius of the circle x² + y² - 6x + 4y - 36 = 0 is (3, - 2) and 7 respectively.
Reason (R) : Centre and radius of the circle x² + y² + 2gx + 2fy + c = 0 is given as (-g, -f) and √g² + f² - c respectively.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.

Correct Answer is Option (a)

2g = - 6
g = - 3
2f = 4
f = 2
Centre = (3, - 2)
and

Question 9: Assertion (A) : In the given figure, XA + AR = XB + BR , where XP, XQ and AB are tangents.

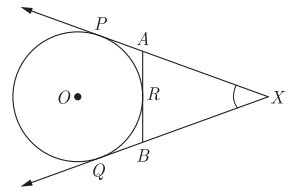
Reason (R) : A tangent to the circle can be drawn from a point inside the circle.

(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.

Correct Answer is Option (c)
We have,  XP = XQ
XA + AP = XB + BQ
XA + AR = XB + BR
[PA = AR and BQ = BR]
(The length of tangents drawn from in external point are equal) So, A is correct but R is incorrect.

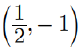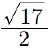Question 10: Assertion (A) : Centre and radius of the circle x2 + y2 - x + 2y - 3 = 0 is and respectively.
Reason (R) : The equation of a circle with radius r having centre (h,k) is given by  (x - h²) + (y - k)² = r².
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.

Correct Answer is Option (b)
2g = - 1
g =
and 2f = 2
f = 1