Poison Distribution | Applied Mathematics for Class 12 - Commerce PDF Download
| Table of contents |

|
| Introduction |

|
| Attributes of a Poisson Experiment |

|
| Notation |

|
| What is Poisson Distribution? |

|
| How to find the Mean and Variance of Poisson Distribution? |

|
| Solved Example |

|
Introduction
A Poisson distribution is known to be the probability distribution that results from a Poisson experiment.
Poisson distribution can actually be an important type of probability distribution formula in Mathematics. As in the binomial distribution, we will not know the number of trials, or the probability of success on a certain trail. The average number of successes (wins) will be given for a certain time interval. The average number of successes is known as “Lambda” and denoted by the symbol λ. In this article, we are going to discuss the Poisson variance formula, equation for Poisson distribution, Poisson probability formula, Poisson probability equation.
Attributes of a Poisson Experiment
A Poisson experiment is known to be a statistical experiment which has the following properties:
- The Poisson experiment generally results in outcomes that can be classified as successes or failures (win or fail).
- The average number of successes is denoted by (μ) that occurs in a specified region is known.
- The probability that success will occur is proportionally equal to the size of the region.
- The probability that success will occur in equal to an extremely small region is virtually zero.
Note that the specified region can take many forms. For instance, it can be a length, a volume, an area, a period of time, etc.
Notation
The following notation given below is helpful when we talk about the Poisson distribution and the Poisson distribution formula.
- e denotes a constant that is equal to approximately 2.71828. (Actually, e is known as the base of the natural logarithm system.)
- μ which denotes the mean number of successes that occur in a specified region.
- x denotes the actual number of successes that occur in a specified region.
- P(x; μ) denotes the Poisson probability and signifies that exactly x successes occur in a Poisson experiment when the mean number of successes is equal to μ.
What is Poisson Distribution?
- A Poisson random variable can be defined as the number of successes that results from a Poisson experiment. The probability distribution of a Poisson random variable is known as a Poisson distribution.
- Given the mean number of successes denotes by μ that occur in a specified region, we can compute the Poisson probability based on the following given formula:
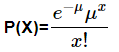
- Poisson Formula. Let’s suppose we conduct a Poisson experiment, in which the average number of successes within a given region is equal to μ. Then, the Poisson probability is:
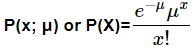
- where x is known to be the actual number of successes that result from the experiment, and the value of the constant e is approximately equal to 2.71828.
The Formula for Poisson Distribution
The probability distribution of a Poisson random variable lets us assume as X. It represents the number of successes that occur in a given time interval or period and is given by the formula:

Where, x=0,1,2,3,…, e=2.71828
μ denotes the mean number of successes in the given time interval or region of space.
How to find the Mean and Variance of Poisson Distribution?
Let’s know how to find the mean and variance of Poisson distribution. If μ is equal to the average number of successes occurring in a given time interval or region in the Poisson distribution. Then we can say that the mean and the variance of the Poisson distribution are both equal to μ.
Therefore, E(X) = μ and V(X) = σ2 = μ
Remember that, in a Poisson distribution, only one parameter, μ is needed to determine the probability of any given event. This is how to find the mean and variance of Poisson distribution.
Poisson Distribution Properties (Poisson Mean and Variance)
- The mean of the distribution is equal to and denoted by μ.
- The variance is also equal to μ.
Some Applications of Poisson Distribution are as Following-
- The number of deaths by horse kicking in the army of Prussian.
- Birth defects and genetic mutations.
- Rare diseases like Leukemia, because it is very infectious and so not independent mainly in legal cases.
- Car accident prediction on roads.
- Traffic flow and the ideal gap distance between vehicles.
- The number of typing errors found on a page in a book.
- Hairs found in McDonald’s hamburgers.
- The spread of an endangered animal in Africa.
- Failure of a machine in one month.
Conditions for Poisson Distribution
- An event can occur any number of times during a time span.
- Events occur independently. In other words, if an event occurs, it does not affect the probability of another event occurring in the same time period.
- The rate of occurrence is constant; that is, the rate does not change based on time.
- The probability of an event occurring is proportional to the length of the time period. For example, it should be twice as likely for an event to occur in a 2 hour time period than it is for an event to occur in a 1 hour period.
Solved Example
Example: The average number of homes sold by the Acme Realty company is 2 homes per day. What will be the probability that exactly 3 number of homes will be sold tomorrow?
This is a Poisson experiment in which we know the following, let’s write down the given data:
(i) μ is equal to 2; since 2 homes are sold per day, on average.
(ii) x is equal to 3; since we want to find the likelihood that 3 homes will be sold tomorrow.
(iii) e is equal to 2.71828; since e is a constant equal to approximately 2.71828.
Now plugging these values into the Poisson formula as follows:, substituting the values of a and μ
P(3; 2) = (2.71828-2) (23) / 3!
P(3; 2) = (0.13534) (8) / 6
P(3; 2) = 0.180
Thus, the probability of selling three numbers of homes tomorrow is equal to 0.180.
|
64 videos|110 docs|63 tests
|














