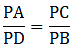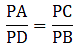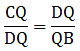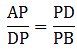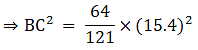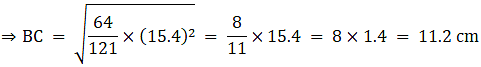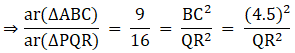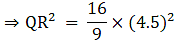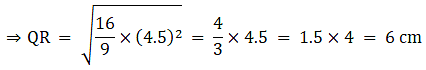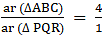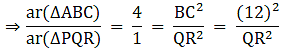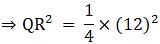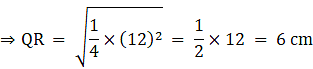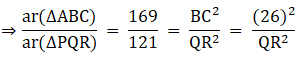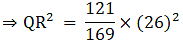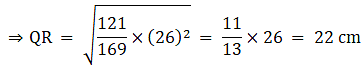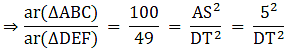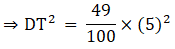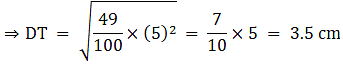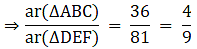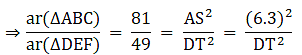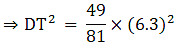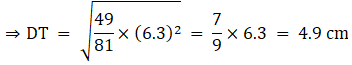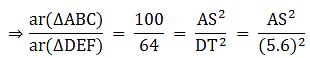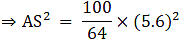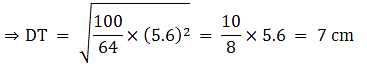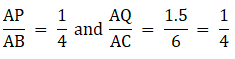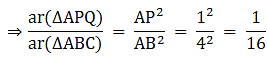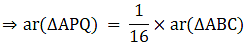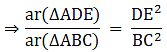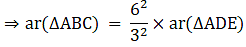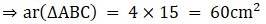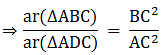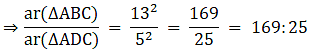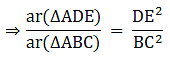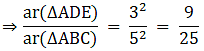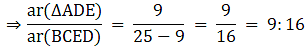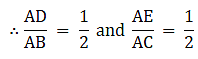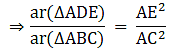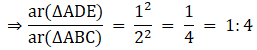RS Aggarwal Solutions: Triangles- 1 | RS Aggarwal Solutions for Class 10 Mathematics PDF Download
Exercise: 4a
Q.1. D and E are points on the sides AB and AC respectively of a ΔABC such that DE || BC.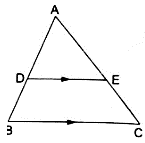
If AD = 3.6 cm, AB = 10 cm and AE = 4.5 cm, find EC and AC.
Given: AD = 3.6 cm, AB = 10 cm and AE = 4.5 cm.
Applying Thale’s Theorem,[∵ DB = AB – AD ⇒ DB = 10 – 3.6 = 6.4]
⇒ EC = 8
Now, AC = AE + EC
⇒ AC = 4.5 + 8 = 12.5
Hence, EC = 8 cm and AC = 12.5 cm
Q.2. D and E are points on the sides AB and AC respectively of a ΔABC such that DE || BC.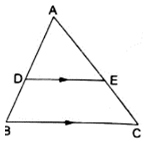
If AB = 13.3 cm, AC = 11.9 cm and EC = 5.1 cm, find AD.
Given: AB = 13.3 cm, AC = 11.9 cm and EC = 5.1 cm.
Applying Thale’s Theorem,
Since we need to find DB first, we add 1 on both sides
⇒ DB = 5.7
AD is given by,
AD = AB – DB
⇒ AD = 13.3 – 5.7
⇒ AD = 7.6 cm
Hence, AD is 7.6.
Q.3. D and E are points on the sides AB and AC respectively of a ΔABC such that DE || BC.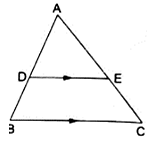
If 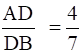 and AC = 6.6 cm, find AE.
and AC = 6.6 cm, find AE.
Given: AD/DB = 4/7 or AD = 4 cm, DB = 7 cm, and AC = 6.6
Applying Thale’s Theorem,
We have AE at RHS but we need AC, as the value of AC is given. So by adding 1 to both sides of the equation, we can get the desired result
⇒ EC = 4.2
AE is given by,
AE = AC – EC
⇒ AE = 6.6 – 4.2
⇒ AE = 2.4
Hence, AE is 2.4 cm.
Q.4. D and E are points on the sides AB and AC respectively of a ΔABC such that DE || BC.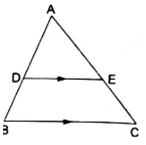
If 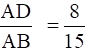 and EC = 3.5 cm, find AE.
and EC = 3.5 cm, find AE.
Given: AD/AB = 8/15 or AD = 8 cm, AB = 15 cm, and EC = 3.5 cm
By applying Thale’s Theorem,
⇒ 8×(AE + 3.5) = 15×AE
⇒ 8×AE + 28 = 15×AE
⇒ 15×AE – 8×AE = 28
⇒ 7×AE = 28
⇒ AE = 28/7 = 4
Hence, AE is 4 cm.
Q.5. D and E are points on the sides AB and AC respectively of a ΔABC such that DE || BC.
Find the value of x, when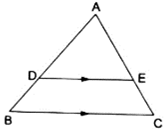
AD = x cm, DB = (x - 2) cm,
AE = (x + 2) cm and EC = (x - 1) cm.
Given: AD = x cm,
DB = (x – 2) cm,
AE = (x + 2) cm and,
EC = (x – 1) cm
By applying Thale’s Theorem,
⇒ x(x – 1) = (x + 2)(x – 2)
⇒ x2 – x = x2 – 4
⇒ x = 4
Thus, x = 4 cm
Q.6. D and E are points on the sides AB and AC respectively of a ΔABC such that DE || BC.
Find the value of x, when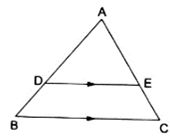
AD = 4 cm, DB = (x - 4) cm, AE = 8 cm and EC = (3x -19) cm.
Given: AD = 4 cm, DB = (x – 4) cm, AE = 8 cm and EC = (3x – 19) cm
By Thale’s theorem,
⇒ 4(3x – 19) = 8(x – 4)
⇒ 12x – 76 = 8x – 32
⇒ 12x – 8x = 76 – 32
⇒ 4x = 44
⇒ x = 44/4 = 11
Thus, x = 11 cm
Q.7. D and E are points on the sides AB and AC respectively of a ΔABC such that DE || BC.
Find the value of x, when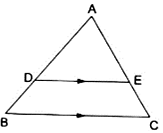
AD = (7x - 4) cm, AE = (5x - 2) cm, DB = (3x + 4) cm and EC = 3x cm.
Given: AD = (7x – 4) cm, AE = (5x – 2), DB = (3x + 4) cm and EC = 3x cm
By Thale’s theorem,
⇒ 3x(7x – 4) = (5x – 2)(3x + 4)
⇒ 21x2 – 12x = 15x2 + 20x – 6x – 8
⇒ 21x2 – 12x = 15x2 + 14x – 8
⇒ 21x2 – 15x2 – 12x – 14x + 8 = 0
⇒ 6x2 – 26x + 8 = 0
⇒ 2×(3x2 – 13x + 4) = 0 [Simplifying the equation]
⇒ 3x2 – 13x + 4 = 0
⇒ 3x2 – 12x – x + 4 = 0
⇒ 3x(x – 4) – (x – 4) = 0
⇒ (3x – 1)(x – 4) = 0
⇒ (3x – 1) = 0 or (x – 4) = 0
⇒ x = 1/3 or x = 4
Now since we’ve got two values of x, that is, 1/3 and 4. We shall check for its feasibility.
Substitute x = 1/3 in AD = (7x – 4), we get
AD = 7×(1/3) – 4 = -1.67, which is not possible since side of a triangle cannot be negative.
Hence, x = 4 cm.
Q.8. D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE || BC or not.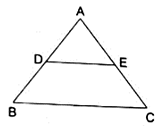
AD = 5.7 cm, DB = 9.5 cm, AE = 4.8 cm and EC = 8 cm.
Here, by applying converse of Thale’s theorem we can conclude whether or not DE ∥ BC.
By Thale’s theorem,
Solving for AD/DB'
Solving for AE/EC'
As equation (i) is equal to equation (ii),
it satisfies Thale’s theorem.
Hence, we can say DE ∥ BC.
Q.9. D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE || BC or not.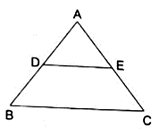
AB = 11.7 cm, AC = 11.2 cm, BD = 6.5 cm and AE = 4.2 cm.
Here, by applying converse of Thale’s theorem we can conclude whether or not DE ∥ BC.
By Thale’s theorem,
Solving for AD/DB'
We need to find AD from given AB = 11.7 cm and BD = 6.5 cm.
AD = AB – BD
⇒ AD = 11.7 – 6.5
⇒ AD = 5.2
Solving for AE/EC'
We need to find EC from given AC = 11.2 cm and AE = 4.2 cm.
EC = AC – AE
⇒ EC = 11.2 – 4.2
⇒ EC = 7
As equation (i) is not equal to equation (ii),
it doesn’t satisfies Thale’s theorem.
Hence, we can say DE not parallel to BC.
Q.10. D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE || BC or not.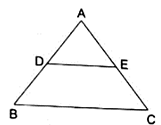
AB = 10.8 cm, AD = 6.3 cm, AC = 9.6 cm and EC = 4 cm.
Here, by applying converse of Thale’s theorem we can conclude whether or not DE ∥ BC.
By Thale’s theorem,
Solving for AD/DB'
We need to find DB from given AB = 10.8 cm and AD = 6.3 cm.
DB = AB – AD
⇒ DB = 10.8 – 6.3
⇒ DB = 4.5
Solving for AE/EC'
We need to find AE from given AC = 9.6 cm and EC = 4 cm.
AE = AC – EC
⇒ AE = 9.6 – 4
⇒ AE = 5.6
As equation (i) is equal to equation (ii),
it satisfies Thale’s theorem.
Hence, we can say DE ∥ BC.
Q.11. D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE || BC or not.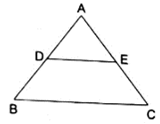
AD = 7.2 cm, AE = 6.4 cm, AB = 12 cm and AC =10 cm.
Here, by applying converse of Thale’s theorem we can conclude whether or not DE ∥ BC.
By Thale’s theorem,
Solving for AD/DB'
We need to find DB from given AB = 12 cm and AD = 7.2 cm.
DB = AB – AD
⇒ DB = 12 – 7.2
⇒ DB = 4.8
Solving for AE/EC'
We need to find EC from given AC = 10 cm and AE = 6.4 cm.
EC = AC – AE
⇒ EC = 10 – 6.4
⇒ EC = 3.6
As equation (i) is not equal to equation (ii),
it doesn’t satisfies Thale’s theorem.
Hence, we can say DE is not parallel to BC.
Q.12. In a ΔABC, AD is the bisector of ∠A.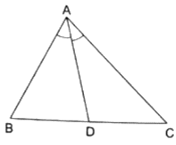
If AB = 6.4 cm, AC = 8 cm and BD = 5.6 cm, find DC.
Given: AB = 6.4 cm, AC = 8 cm and BD = 5.6 cm
Since AD bisects ∠A, we can apply angle-bisector theorem in ∆ABC,
Substituting given values, we get
⇒ DC = 7
Thus, DC is 7 cm.
Q.13. In a ΔABC, AD is the bisector of ∠A.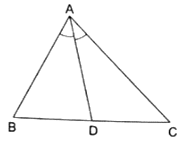
If AB = 10 cm, AC = 14 cm and BC =6 cm, find BD and DC.
Given: AB = 10 cm, AC = 14 cm and BC = 6 cm
Since AD bisects ∠A, we can apply angle-bisector theorem in ∆ABC,
Substituting given values, we get
To find BD and DC,
Let BD = x cm, and it’s given that BC = 6 cm, then DC = (6 – x) cm
Then
⇒ 14x = 10(6 – x)
⇒ 14x = 60 – 10x
⇒ 14x + 10x = 60
⇒ 24x = 60
⇒ x = 60/24 = 2.5
⇒ BD = 2.5 cm
If BD = 2.5 cm and BC = 6 cm, then DC = (6 – x) = (6 – 2.5) = 3.5
Thus, BD is 2.5 cm and DC = 3.5 cm.
Q.14. In a ΔABC, AD is the bisector of ∠A.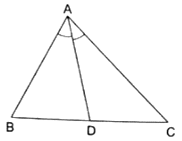
If AB = 5.6 cm, BD = 3.2 cm and BC = 6 cm, find AC.
Given: AB = 5.6 cm, BC = 6 cm and BD = 3.2 cm
Since AD bisects ∠A, we can apply angle-bisector theorem in ∆ABC,
Substituting given values, we get
Here, DC is given by
DC = BC – BD
⇒ DC = 6 – 3.2 = 2.8
⇒ AC = 4.9
Thus, AC is 4.9 cm.
Q.15. In a ΔABC, AD is the bisector of ∠A.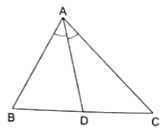
If AB = 5.6 cm, AC = 4 cm and DC = 3 cm, find BC.
Given: AB = 5.6 cm, AC = 4 cm and DC = 3 cm
Since AD bisects ∠A, we can apply angle-bisector theorem in ∆ABC,Substituting given values, we get
⇒ BD = 4.2
Now, BC = BD + DC
⇒ BC = 4.2 + 3 = 7.2
Thus, BC is 7.2 cm.
Q.16. M is a point on the side BC of a parallelogram ABCD. DM, when produced, meets AB produced at N. Prove that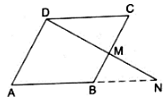
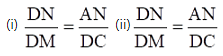
(i). Given: ABCD is a parallelogram.
To Prove:
Proof: In ∆DMC and ∆NMB,
∠DMC = ∠NMB [∵ they are vertically opposite angles]
∠DCM = ∠NBM [∵ they are alternate angles]
∠CDM = ∠MNB [∵ they are alternate angles]
By AAA-similarity, we can say
∆DMC ∼ ∆NMB
So, from similarity of the triangle, we can sayHence, proved.
(ii). Given: ABCD is a parallelogram.
To Prove:
Proof: As we have already derived
Add 1 on both sides of the equation, we get[∵ ABCD is a parallelogram and a parallelogram’s opposite sides are always equal ⇒ DC = AB]
Hence, proved.
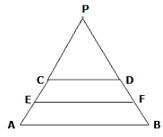
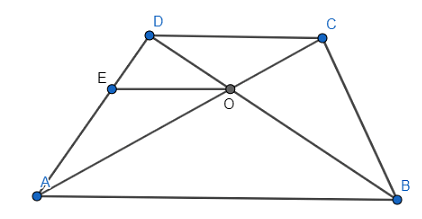
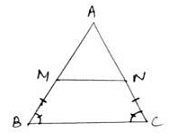
Q.17. Show that the line segment which joins the midpoints of the oblique sides of a trapezium is parallel to the parallel sides.
We can draw the trapezium as
Here, let EF be the line segment joining the oblique sides of the trapezium at midpoints E and F (say) correspondingly.
Construction: Extend AD and BC such that it meets at P.
To Prove: EF ∥ DC and EF ∥ AB
Proof: Given that, ABCD is trapezium which means DC ∥ AB. …(statement (i))
In ∆PAB,
DC ∥ AB (by statement (i))
So, this means we can apply Thale’s theorem in ∆PAB. We get
∵ E and F are midpoints of AD and BC respectively, we can write
DA = DE + EA
Or DA = 2DE …(iii)
CB = CF + FB
Or CB = 2CF …(iv)
Substituting equation (iii) and (iv) in equation (ii), we get
By applying converse of Thale’s theorem, we can write DC ∥ EF.
Now if DC ∥ EF, and we already know that DC ∥ AB.
⇒ EF is also parallel to AB, that is, EF ∥ AB.
This means, DC ∥ EF ∥ AB.
Hence, proved.
Q.18. In the adjoining figure, ABCD is a trapezium in which CD || AB and its diagonals intersect at O. If AO = (5x – 7) cm, OC = (2x + 1) cm, DO = (7x – 5) cm and OB = (7x + 1) cm, find the value of x.
Given: In the adjoining figure, ABCD is a trapezium in which CD || AB and its diagonals intersect at O. If AO = (5x – 7) cm, OC = (2x + 1) cm, DO = (7x – 5) cm and OB = (7x + 1) cm.
To find: the value of x.
In the trapezium ABCD, AB || DC and its diagonals intersect at O.
Through O draw EO || AB meeting AD at E.
Now In Δ ADC
As EO || AB || DC
By thales theorem which states that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points then the other two sides are divided in the same ratio.
In Δ DAB,
EO || AB
By thales theorem,
From (i) and (ii)
Put the given values as:
⇒ (5x – 7)(7x + 1) = (7x – 5)(2x + 1)
⇒ 35x2 + 5x – 49x – 7 = 14x2 – 10x + 7x – 5
⇒ 35x2 – 44x – 7 = 14x2 – 3x – 5
⇒ 35x2 – 14x2 – 44x + 3x – 7 + 5 = 0
⇒ 21x2 – 41x – 2 = 0
⇒ 21x2 – 42x + x – 2 = 0
⇒ 21x(x – 2) + (x – 2) = 0
⇒ (21x + 1)(x – 2) = 0
⇒ (21x + 1) = 0 or (x – 2) = 0
⇒ x = -1/21 or x = 2
But x = -1/21 doesn’t satisfy the length of intersected lines.
So x ≠ -1/21
And thus, x = 2.
Q.19. In a ΔABC, M and N are points on the sides AΔB and AC respectively such that BM = CN. If ∠B = ∠C then show that MN || BC.
We have
To show that, MN ∥ BC.
Given that, ∠B = ∠C and BM = CN.
So, AB = AC [sides opposite to equal angles (∠B = ∠C) are equal]
Subtract BM from both sides, we get
AB – BM = AC – BM
⇒ AB – BM = AC – CN
⇒ AM = AN
⇒ ∠AMN = ∠ANM
[angles opposite to equal sides (AM = AN) are equal] …(i)
We know in ∆ABC,
∠A + ∠B + ∠C = 180° [∵ sum of angles of a triangle is 180°] …(ii)
And in ∆AMN,
∠A + ∠AMN + ∠ANM = 180° [∵ sum of angles of a triangle is 180°] …(iii)
Comparing equations (ii) and (iii), we get
∠A + ∠B + ∠C = ∠A + ∠AMN + ∠ANM
⇒ ∠B + ∠C = ∠AMN + ∠ANM
⇒ 2∠B = 2∠AMN [∵ from equation (i), and also ∠B = ∠C]
⇒ ∠B = ∠AMN
Thus, MN ∥ BC since the corresponding angles, ∠AMN = ∠B.
Q.20. ΔABC and ΔDBC lie on the same side of BC, as shown in the figure. From a point, P on BC, PQ || AB and PR || BD are drawn, meeting AC at Q and CD at R respectively. Prove that QR || AD.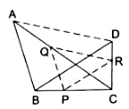
We can observe two triangles in the figure.
In ∆ABC,
PQ ∥ AB
Applying Thale’s theorem, we get
In ∆BDC,
PR ∥ BP
Applying Thale’s theorem, we get
Comparing equations (i) and (ii),
Now, applying converse of Thale’s theorem, we get
QR ∥ AD
Hence, QR is parallel to the AD.
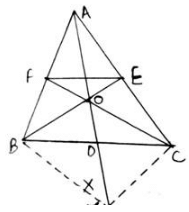
Q.21. In the given figure, side BC of ΔABC is bisected at D and O is any point on the AD. BO and CO produced meet AC and AB at E and F respectively, and the AD is produced to X so that D is the midpoint of OX. Prove that AO: AX = AF: AB and show that EF || BC.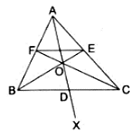
We have the diagram as,
Given: BD = DC & OD = DX
To Prove:and also, EF ∥ BC
Proof: Since, from the diagram we can see that diagonals OX and BC bisect each other in quadrilateral BOCX. Thus, BOCX is a parallelogram.
If BOCX is a parallelogram, BX ∥ OC, and BO ∥ CX.
⇒ BX ∥ FC (as OC extends to FC) and CX ∥ BE (BO extends to BE)
⇒ BX ∥ OF and CX ∥ OE
∵ BX ∥ OF, applying Thale’s theorem in ∆ABX, we get
Now since CX ∥ OE, applying Thale’s theorem in ∆ACX, we get
By equations (i) and (ii), we get
By applying converse of Thale’s theorem in the above equation, we can write
EF ∥ BC
Hence, proved.
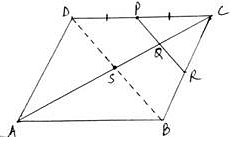
Q.22. ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ = 1/4 AC. If PQ produced meets BC at R, prove that R is the midpoint of BC.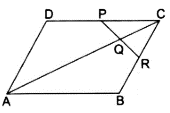
We have the diagram as
Given: DP = PC &
CQ = (1/4)AC …(i)
To Prove: CR = RB
Proof: Join B to D
As diagonals of a parallelogram bisect each other at S.
Dividing equation (i) by (ii), we get
⇒ CQ = CS/2
⇒ Q is the midpoint of CS.
According to midpoint theorem in ∆CSD, we have
PQ ∥ DS
Similarly, in ∆CSB, we have
QR ∥ SB
Also, given that CQ = QS
We can conclude that, by the converse of midpoint theorem, CR = RB.
That is, R is the midpoint of CB.
Hence, proved.
Q.23. In the adjoining figure, ABC is a triangle in which AB = AC. If D and E are points on AB and AC respectively such that AD = AE, show that the points B, C, E and D are concyclic.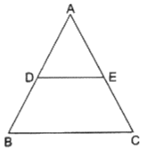
Given: AD = AE …(i)
& AB = AC …(ii)
Subtracting AD from both sides of equation (ii), we get
AB – AD = AC – AD
⇒ AB – AD = AC – AE [from equation (i)]
⇒ DB = EC [∵ AB – AD = DB & AC – AE = EC] …(iii)
Now, divide equation (i) by (iii), we get
By converse of Thale’s theorem, we can conclude by this equation that DE ∥ BC.
So, ∠DEC + ∠ECB = 180° [∵ sum of interior angles on the same transversal line is 180°]
Or ∠DEC + ∠DBC = 180° [∵ AB = AC ⇒ ∠C = ∠B]
Hence, we can write DEBC is cyclic and points D, E, B and C are concyclic.
Q.24. In ΔABC, the bisector of ∠B meets AC at D. A line PQ || AC meets AB, BC, and BD at P, Q and R respectively.
Show that PR x BQ = QR x BP.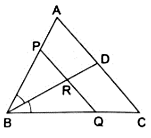
Given: ∠PBR = ∠QBR & PQ ∥ AC.
In ∆BQP,
BR bisects ∠B such that ∠PBR = ∠QBR.
Since angle-bisector theorem says that, if two angles are bisected in a triangle then it equates their relative lengths to the relative lengths of the other two sides of the triangles.
So by applying angle-bisector theorem, we get
⇒ QR × BP = PR × BQ
Hence, proved.
Exercise: 4b
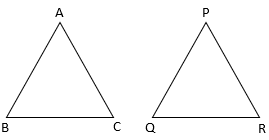
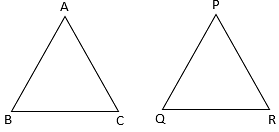
Q.1. In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form.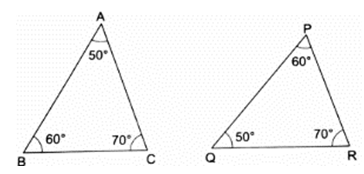
In these triangles ABC and PQR, observe that
∠BAC = ∠PQR = 50°
∠ABC = ∠QPR = 60°
∠ACB = ∠PRQ = 70°
Thus, by angle-angle-angle similarity, i.e., AAA similarity,
∆ABC ∼ ∆PQR
Q.2. In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form.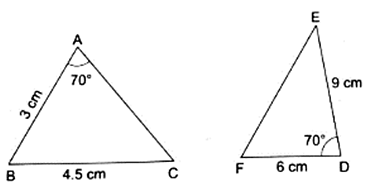
In triangles ABC & EFD,
∠ABC ≠ ∠EDF
So, clearly, since no criteria satisfies, ∆ABC is not similar to ∆EFD.
Q.3. In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form.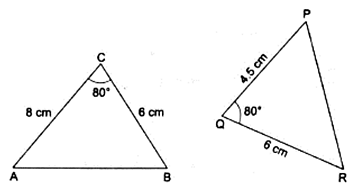
In triangles ABC & PQR,
∠ACB = ∠PQR
By SAS criteria, we can say
∆ABC ∼ ∆PQR
Q.4. In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form.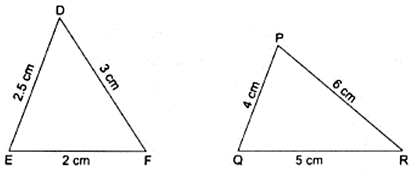
In triangles DEF & PQR,
By SSS criteria, we can write
∆DEF ∼ ∆PQR
Q.5. In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form.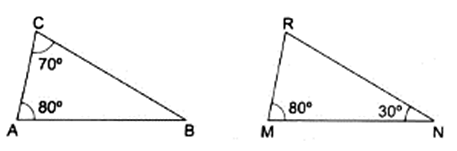
In ∆ABC, we can find ∠ABC.
∠ABC + ∠BCA + ∠CAB = 180° [∵ sum of all the angles of a triangle is 180°]
⇒ ∠ABC + 70° + 80° = 180°
⇒ ∠ABC + 150° = 180°
⇒ ∠ABC = 180° - 150°
⇒ ∠ABC = 30°
We can observe from triangles ABC & MNR,
∠ABC = ∠MNR
∠CAB = ∠RMN
Hence, by AA similarity we can say, ∆ABC ∼ ∆MNR
Q.6. In the given figure, ΔODC ~ ΔOBA, ∠BOC = 115° and ∠CDO = 70°.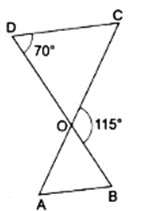
Find (i) ∠DOC (ii) ∠DCO (iii) ∠OAB (iv) ∠OBA.
(i) To find ∠DOC, we can observe the straight line DB.
∠DOC + ∠COB = 180° [∵ sum of all angles in a straight line is 180°]
⇒ ∠DOC + 115° = 180°
⇒ ∠DOC = 180° - 115°
⇒ ∠DOC = 65°
(ii) In ∆DOC,
And given that, ∠CDO = 70°, ∠DOC = 65° (from (i))
∠DOC + ∠DCO + ∠CDO = 180°
⇒ 65° + ∠DCO + 70° = 180°
⇒ ∠DCO + 135° = 180°
⇒ ∠DCO = 180° - 135°
⇒ ∠DCO = 45°
(iii) We have derived ∠DCO from (ii), ∠DCO = 45°
Thus, ∠OAB = 45° [∵ ∠OAB = ∠DCO as ∆ODC ∼ ∆OBA]
(iv) It’s given that, ∠CDO = 70°
Thus, ∠OBA = 70° [∵ ∠OBA = ∠CDO as ∆ODC ∼ ∆OBA]
Q.7. In the given figure, ΔOAB ~ ΔOCD. If AB = 8 cm, BO = 6.4 cm, OC = 3.5 cm and CD = 5 cm, find (i) OA (ii) DO.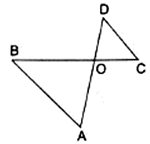
(i). Given that, AB = 8 cm
BO = 6.4 cm,
OC = 3.5 cm
& CD = 5 cm
∆OAB ∼ ∆OCD
When two triangles are similar, they can be written in the ratio as
Substitute gave values in the above equations,
⇒ OA = 5.6
Thus, OA = 5.6 cm
(ii). Given that, AB = 8 cm
BO = 6.4 cm,
OC = 3.5 cm
& CD = 5 cm
∆OAB ∼ ∆OCD
When two triangles are similar, they can be written in the ratio as
Substitute gave values in the above equations,
⇒ DO = 4
Thus, DO = 4 cm
Q.8. In the given figure, if ∠ADE = ∠B, show that ΔADE ~ ΔABC. If AD = 3.8 cm, AE = 3.6 cm, BE= 2.1 cm and BC = 4.2 cm, find DE.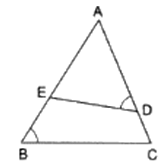
Given is that ∠ADE = ∠B
From the diagram clearly, ∠EAD = ∠BAC [∵ they are common angles]
Now, since two of the angles are correspondingly equal. Then by AA similarity criteria, we can say
∆ADE ∼ ∆ABC
Further, it’s given that
AD = 3.8 cm
AE = 3.6 cm
BE = 2.1 cm
BC = 4.2 cm
DE =?
To find AB, we can express it in the form AB = AE + BE = 3.6 + 2.1
⇒ AB = 5.7
So for the condition that ∆ADE ∼ ∆ABC,
Substituting given values in the above equation,
⇒ DE = 2.8
Thus, DE = 2.8 cm
Q.9. The perimeters of two similar triangles ABC and PQR are 32 cm and 24 cm respectively. If PQ = 12 cm, find AB.
Given that, ∆ABC ∼ ∆PQR
And perimeter of ∆ABC = 32 cm & perimeter of ∆PQR = 24 cm
We can write relationship as,
⇒ AB = 16
Thus, AB = 16 cm.
Q.10. The corresponding sides of two similar triangles ABC and DEF are BC = 9.1 cm and EF = 6.5 cm. If the perimeter of ΔDEF is 25 cm, find the perimeter of ΔABC.
Given that, ∆ABC ∼ ∆DEF
Also, BC = 9.1 cm & EF = 6.5 cm
And perimeter of ∆DEF = 25 cm
We need to find perimeter of ∆ABC = ?
We can write relationship as,
⇒ perimeter of ∆ABC = 35
Thus, perimeter of ∆ABC = 35 cm
Q.11. In the given figure, ∠CAB = 90° and AD ± BC. Show that ΔBDA ~ ΔBAC. If AC = 75 cm, AB = 1 m and BC = 1.25 m, find AD.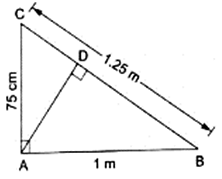
Given that, ∠CAB = 90°
AC = 75 cm
AB = 1 m
BC = 1.25 m
To show that, ∆BDA ∼ ∆BAC
In the diagram, we can see
∠BDA = ∠BAC = 90°
∠DBA = ∠CBA [They are common angles]
So by AA-similarity theorem,
∆BDA ∼ ∆BAC
Thus, now since ∆BDA ∼ ∆BAC, we can write as[∵ AC = 75 cm, AB = 1 m = 100 cm & BC = 1.25 m = 125 cm]
⇒ AD = 60 cm
Hence, AD = 60 cm or 0.6 m
Q.12. In the given figure, ∠ABC = 90° and BD ⊥ AC. If AB = 5.7 cm, BD = 3.8 cm and CD = 5.4 cm, find BC.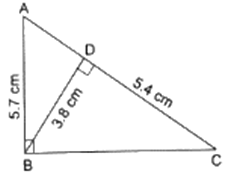
Given that, ∠ABC = 90°
AB = 5.7 cm
BD = 3.8 cm
CD = 5.4 cm
In order to find BC, we need to prove that ∆BDC and ∆ABC are similar.
∠BDC = ∠ABC = 90°
∠ACB = ∠DCB [They are common angles]
By this we have proved ∆BDC ∼ ∆ABC, by AA-similarity criteria.
So we can write,
⇒ BC = 8.1
Hence, BC = 8.1 cm.
Q.13. In the given figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm, AD = 4 cm, find CD.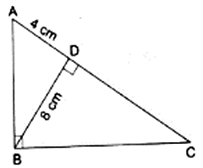
Given that, ∠ABC = 90°
AD = 4 cm
BD = 8 cm
In order to find CD, we need to prove that ∆BDC and ∆ABC are similar.
∠BDC = ∠ADB = 90°
∠DBA = ∠DCB
We have proved ∆DBA ∼ ∆DCB, by AA-similarity criteria.
So we can write,
⇒ CD = 16
Hence, CD = 16 cm.
Q.14. P and Q are points on the sides AB and AC respectively of a ΔABC. If AP = 2 cm, PB = 4 cm, AQ = 3 cm and QC = 6 cm, show that BC = 3PQ.
There are two triangles here, ∆APQ and ∆ABC. We shall prove these triangles to be similar.
Also, ∠A = ∠A [common angle]
So by AA-similarity criteria,
∆APQ ∼ ∆ABC
Thus,
And we know
⇒ BC = 3×PQ
Hence, proved.
Q.15. ABCD is a parallelogram and E is a point on BC. If the diagonal BD intersects AE at F, prove that AF × FB = EF × FD.
Given that, AB ∥ DC & AD ∥ BC
To Prove: AF × FB = EF × FD
Proof: In ∆DAF & ∆BEF
∠DAF = ∠BEF [∵ they are alternate angles]
∠AFD = ∠EFB [∵ they are vertically opposite angles]
This implies that ∆DAF ∼ ∆BEF by AA-similarity criteria.
Now cross-multiply them,
AF × FB = FD × EF
Hence, proved.
Q.16. In the given figure, DB ⊥ BC, DE ⊥ AB, and AC ⊥ BC.
Prove that 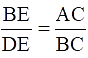
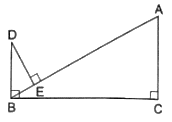
Observe in ∆BED & ∆ACB, we have
∠BED = ∠ACB = 90°
Now according to what’s given, DB ┴ BC and AC ┴ BC we can write,
∠B + ∠C = 180°
This clearly means BD ∥ CA
⇒ ∠EBD = ∠CAB [They are alternate angles]
AA Similarity theorem: The postulate states that two triangles are similar if they have two corresponding angles that are congruent or equal in measure.
Thus, by AA-similarity theorem, ∆BED ∼ ∆ACB
Now, by property of similarity of triangles,
Cross-multiplying, we get,
Hence, proved.
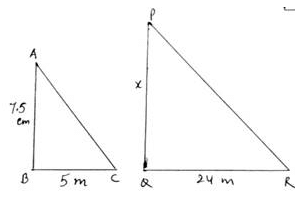
Q.17. A vertical pole of length 7.5 m casts a shadow 5 m long on the ground and at the same time a tower casts a shadow 24 m long. Find the height of the tower.
We have
Let the two triangles be ∆ABC and ∆PQR.
Given that, AB = 7.5 cm
BC = 5 m = 500 cm
QR = 24 m = 2400 cm
We have to find PQ = x (say).
We need to prove ∆ABC is similar to ∆PQR.
We can observe that,
∠ABC = ∠PQR = 90°
∠ACB = ∠PRQ [∵ the sum castes same angle at all places at the same time]
Thus, by AA-similarity criteria, we can say
∆ABC ∼ ∆PQR
So,
Substitute the given values in this equation,
⇒ x = 36 cm
Thus, height of the tower is 36 cm.
Q.18. In an isosceles ΔABC, the base AB is produced both ways in P and Q such that AP × BQ = AC2. Prove that ΔACP ~ ΔBCQ.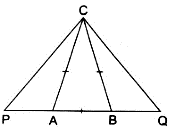
To prove: ∆ACP ∼ ∆BCQ
Proof:
Given that, ∆ABC is an isosceles triangle. ⇒ AC = BC
Also, if ∆ABC is an isosceles triangle,
then ∠CAB = ∠CBA …(i)
Subtracting it by 180° from both sides, we get
180° - ∠CAB = 180° - ∠CBA
⇒ ∠CAP = ∠CBQ …(ii)
Also, given that AP × BQ = AC × AC
Recollecting equations (i), (ii) and (iii),
By SAS-similarity criteria, we get
∆ACP ∼ ∆BCQ
Hence, proved.
Q.19. In the given figure, ∠1 = ∠2 and 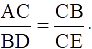 Prove that ΔACB ~ ΔDCE.
Prove that ΔACB ~ ΔDCE.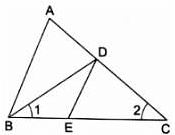
To Prove: ∆ACB ∼ ∆DCE
Proof:
Given that, ∠1 = ∠2
⇒ ∠DBC = ∠DCE
Also in ∆ABC & ∆DCE, we get
∠DCE = ∠ACB [they are common angles to both triangles][∵ BD = DC as ∠1 = ∠2]
Thus by SAS-similarity criteria, we get
∆ACB ∼ ∆DCE
Hence, proved.
Q.20. ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the midpoints of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
Given: AD = BC
P, Q, R and S are the midpoints of AB, AC, CD and BD respectively.
So in ∆ABC, if P and Q are midpoints of AB and A respectively ⇒ PQ ∥ BC
And PQ = (1/2)BC …(i)
Similarly in ∆ADC,
QR = (1/2)AD …(ii)
In ∆BCD,
SR = (1/2)BC …(iii)
In ∆ABD,
PS = (1/2)AD = (1/2)BC [∵ AD = BC]
Using equations (i), (ii), (iii) & (iv), we get
PQ = QR = SR = PS
All these sides are equal.
⇒ PQRS is a rhombus.
Hence, shown that PQRS is a rhombus.
Q.21. In a circle, two chords AB and CD intersect at a point P inside the circle. Prove that
(a) ΔPAC ~ ΔPDB (b) PA • PB = PC • PD.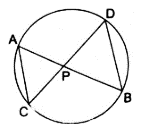
Given: AB and CD are chords of the circle, intersecting at point P.
(a). To Prove: ∆PAC ∼ ∆PDB
Proof: In ∆PAC and ∆PDB,
∠APC = ∠DPB [∵ they are vertically opposite angles]
∠CAP = ∠PDB [∵ angles in the same segment are equal]
Thus, by AA-similarity criteria, we can say that,
∆PAC ∼ ∆PDB
Hence, proved.
(b). To Prove: PA × PB = PC × PD
Proof: As already proved that ∆PAC ∼ ∆PDB
We can write as,
By cross-multiplying, we get
PA × PB = PC × PD
Hence, proved.
Q.22. Two chords AB and CD of a circle intersect at a point P outside the circle. Prove that
(a) ΔPAC ~ ΔPDB (b) PA • PB = PC • PD.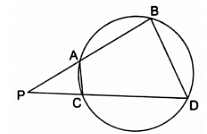
Given: AB and CD are chords of a circle intersecting at point P outside the circle.
(a). To Prove: ∆PAC ∼ ∆PDB
Proof: We know
∠ABD + ∠ACD = 180° [∵ opposite angles of cyclic quadrilateral are supplementary] …(i)
∠PCA + ∠ACD = 180° [∵ they are linear pair angle] …(ii)
Comparing equations (i) & (ii), we get
∠ABD + ∠ACD = ∠PCA + ∠ACD
⇒ ∠ABD = ∠PCA
Also, ∠APC = ∠BPD [∵ they are common angles]
Thus, by AA-similarity criteria, ∆PAC ∼ ∆PDB
Hence, proved.
(b). To Prove: PA × PB = PC × PD
Proof: We have already proved that, ∆PAC ∼ ∆PDB
Thus the ratios can be written as,
By cross-multiplication, we get
PA × PB = PC × PD
Hence, proved.
Q.23. In a right triangle ABC, right-angled at B, D is a point on hypotenuse such that BD ⊥ AC. If DP ⊥ AB and DQ ⊥ BC then prove that (a) DQ2 = DP • QC (b) DP2 = DQ • AP.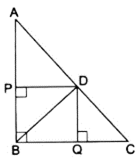
By the property that says, if a perpendicular is drawn from the vertex of a right triangle to the hypotenuse then the triangles on both the sides of the perpendicular are similar to the whole triangle and also to each other.
We can conclude by the property in ∆BDC,
∆CQD ∼ ∆DQB
(a). To Prove: DQ2 = DP × QC
Proof: As already proved, ∆CQD ∼ ∆DQB
We can write the ratios as,
By cross-multiplication, we get
DQ2 = QB × QC …(i)
Now since, quadrilateral PDQB forms a rectangle as all angles are 90° in PDQB.
⇒ DP = QB & PB = DQ
And thus replacing QB by DP in equation (i), we get
DQ2 = DP × QC
Hence, proved.
(b). To Prove: DP2 = DQ × AP
Prof: Similarly using same property, we get
∆APD ∼ ∆DPB
We can write the ratios as,
By cross-multiplication, we get
DP2 = PB × AP
⇒ DP2 = DQ × AP [∵ PB = DQ]
Hence, proved.
Exercise: 4c
Q.1. ΔABC ~ ΔDEF and their areas are respectively 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC.
We know that if two triangles are similar then the ratio of their areas is equal to the ratio of the squares of their corresponding sides.
Q.2. The areas of two similar triangles ABC and PQR are in the ratio 9 : 16. If BC = 4.5 cm, find the length of QR.
We know that if two triangles are similar then the ratio of their areas is equal to the ratio of the squares of their corresponding sides.
Q.3. ΔABC ~ ΔPQR and ar (ΔABC) = 4ar (ΔPQR). If BC = 12 cm, find QR.
Given that
We know that if two triangles are similar then the ratio of their areas is equal to the ratio of the squares of their corresponding sides.
Q.4. The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, find the longest side of the smaller triangle.
Let the two triangles be ABC and PQR and their longest sides are BC and QR.
We know that if two triangles are similar then the ratio of their areas is equal to the ratio of the squares of their longest sides.
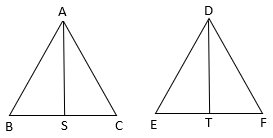
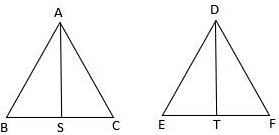
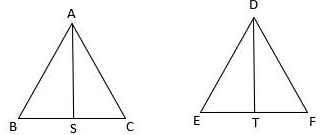
Q.5. ΔABC ~ΔDEF and their areas are respectively 100 cm2 and 49 cm2. If the altitude of ΔABC is 5 cm, find the corresponding altitude of ΔDEF.
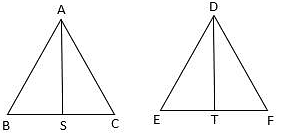
Let the two triangles ABC and DEF have their altitudes as AS and DT.
We know that if two triangles are similar then the ratio of their areas is equal to the ratio of the squares of their corresponding altitudes.
Q.6. The corresponding altitudes of two similar triangles are 6 cm and 9 cm respectively. Find the ratio of their areas.
Let the two triangles ABC and DEF have their altitudes as AS and DT.
We know that if two triangles are similar then the ratio of their areas is equal to the ratio of the squares of their corresponding altitudes.
Q.7. The areas of two similar triangles are 81 cm2 and 49 cm2 respectively. If the altitude of the first triangle is 6.3 cm, find the corresponding altitude of the other.
Let the two triangles ABC and DEF have their altitudes as AS and DT.
We know that if two triangles are similar then the ratio of their areas is equal to the ratio of the squares of their corresponding altitudes.
Q.8. The areas of two similar triangles are 100 cm2 and 64 cm2 respectively. If a median of the smaller triangle is 5.6 cm, find the corresponding median of the other.
Let the two triangles ABC and DEF have their medians as AS and DT.
We know that if two triangles are similar then the ratio of their areas is equal to the ratio of the squares of their corresponding medians.
Q.9. In the given figure, ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm, PB = 3 cm, AQ = 1.5 cm, QC = 4.5 cm, prove that area of ΔAPQ is 1/16 of the area of ΔABC.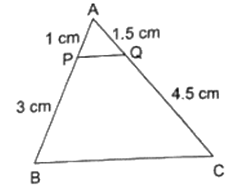
We have
Also ∠ A = ∠ A
So, by SAS similarity criterion ΔAPQ ~ ΔABC
We know that if two triangles are similar then the ratio of their areas is equal to the ratio of the squares of their corresponding sides.
Hence, proved.
Q.10. In the given figure, DE || BC. If DE = 3 cm, BC = 6 cm and ar (ΔADE) = 15 cm2, find the area of ΔABC.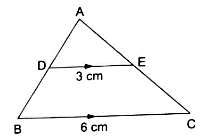
It is given that DE || BC
∴∠ ADE = ∠ ABC (Corresponding angles)
∠ AED = ∠ ACB (Corresponding angles)
So, by AA similarity criterion ΔADE ~ ΔABC
We know that if two triangles are similar then the ratio of their areas is equal to the ratio of the squares of their corresponding sides.
Hence, proved.
Q.11. ΔABC is right-angled at A and AD ⊥ BC. If BC = 13 cm and AC = 5 cm, find the ratio of the areas of ΔABC and ΔADC.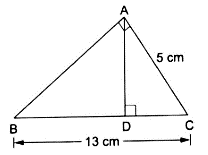
In ΔABC and ΔADC
∴∠ BAC = ∠ ADC (90° angle)
∠ ACB = ∠ ACD (Common)
So, by AA similarity criterion ΔADC ~ ΔABC
We know that if two triangles are similar then the ratio of their areas is equal to the ratio of the squares of their corresponding sides.
Q.12. In the given figure and DE : BC = 3: 5. Calculate the ratio of the areas of ΔADE and the trapezium BCED.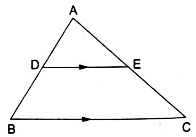
It is given that DE || BC
∴∠ ADE = ∠ ABC (Corresponding angles)
∠ AED = ∠ ACB (Corresponding angles)
So, by AA similarity criterion ΔADE ~ ΔABC
We know that if two triangles are similar then the ratio of their areas is equal to the ratio of the squares of their corresponding sides.
Hence, proved.
Q.13. In ΔABC, D and E are the midpoints of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.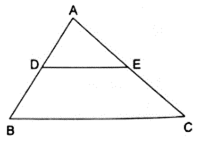
In ΔABC and ΔADE
It is given that AD = DB and AE = EC
Also ∠ A = ∠ A
So, by SAS similarity criterion ΔADE ~ ΔABC
We know that if two triangles are similar then the ratio of their areas is equal to the ratio of the squares of their corresponding sides.
|
53 docs|15 tests
|
|
53 docs|15 tests
|

|
Explore Courses for Class 10 exam
|

|
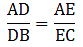
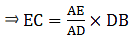
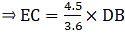 [∵ DB = AB – AD ⇒ DB = 10 – 3.6 = 6.4]
[∵ DB = AB – AD ⇒ DB = 10 – 3.6 = 6.4]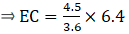
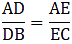
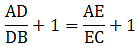
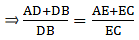
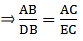
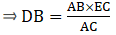
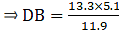
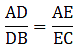
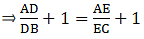
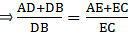
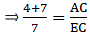
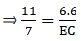
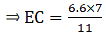
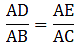
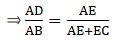
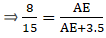
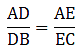
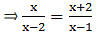
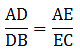
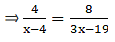
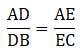
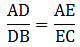
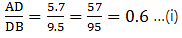
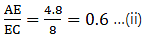
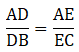
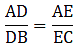
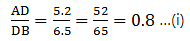
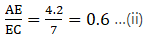
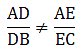
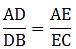
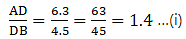
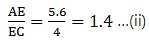
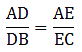
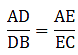
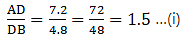
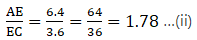
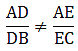
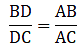
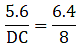
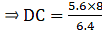
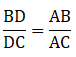
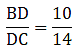
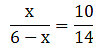
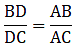
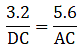
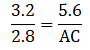
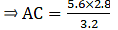
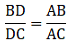
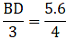
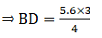
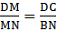
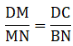
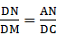
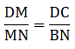
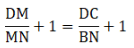
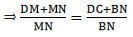
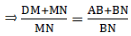 [∵ ABCD is a parallelogram and a parallelogram’s opposite sides are always equal ⇒ DC = AB]
[∵ ABCD is a parallelogram and a parallelogram’s opposite sides are always equal ⇒ DC = AB]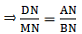
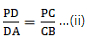
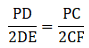
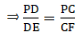
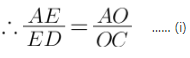
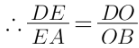
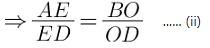
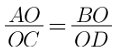
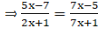
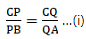
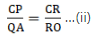
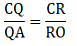
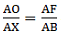 and also, EF ∥ BC
and also, EF ∥ BC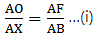
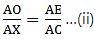
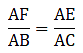
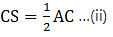
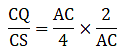
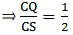
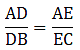
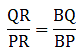
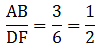
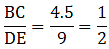
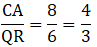
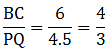
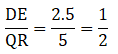
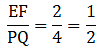
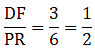
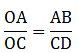
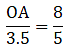
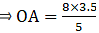
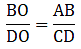
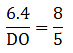
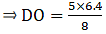
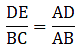
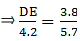
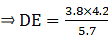
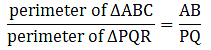
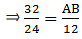
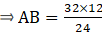
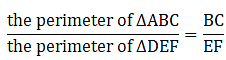
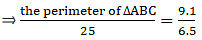
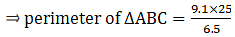
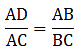
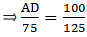 [∵ AC = 75 cm, AB = 1 m = 100 cm & BC = 1.25 m = 125 cm]
[∵ AC = 75 cm, AB = 1 m = 100 cm & BC = 1.25 m = 125 cm]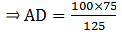
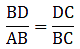
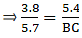
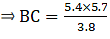
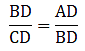
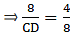
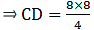
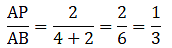
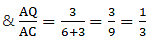
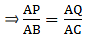
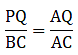
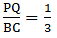
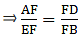
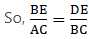
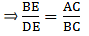
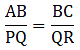
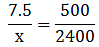
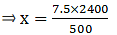
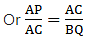
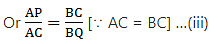
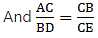
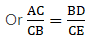
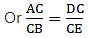 [∵ BD = DC as ∠1 = ∠2]
[∵ BD = DC as ∠1 = ∠2]