RS Aggarwal Solutions: Constructions- 2 | RS Aggarwal Solutions for Class 10 Mathematics PDF Download
Formative Assessment (unit Test)
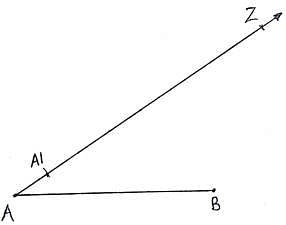
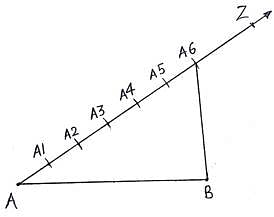
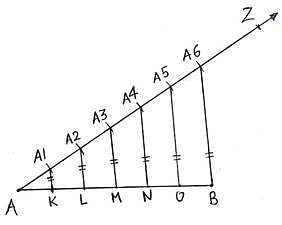
Q.1. Draw a line segment AB of length 5.4 cm. Divide it into six equal parts. Write the steps of construction.
Steps of Construction:
1. Draw a line segment AB of given length 5. 4cm.
2. Draw a ray, AZ, originating from A and making an acute angle with line segment AB.
3. Taking A as center draw an arc cutting at A1 on the ray.
4. As we have to divide the line into 6 equal parts, With the same radius and taking A1 as center draw another arc on the ray.
5. Repeat till we get A6.
6. Join A6 with B.
7. Now draw lines parallel to A6B from A1,A2,A3,A4 and A5 as well, which cut the line segment AB at K,L,M,N and O respectively.
8. Then AK,KL,LM,MN,NO,OB are the required 6 equal parts of line AB.
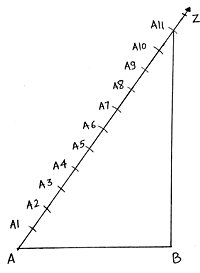
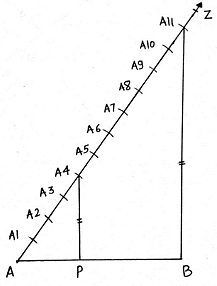
Q.2. Draw a line segment AB of length 6. 5 cm and divide it in the ratio 4 : 7. Measure each of the two parts.
Steps of Construction:
1. Draw a line segment AB of length 6. 5cm.
2. Draw a ray AZ making an acute angle with the line AB.
3. As we have to divide the line in the ratio of 4 : 7. So we will make 4 + 7 = 11 points along AZ.
4. Along AZ we mark 11 arcs taking A as starting point for the first, A1 as starting point for second and so on till A11.
5. Join the A11B.
6. With the help of these arcs this line can be divided into 11 equal points.
7. In our case of 4 : 7, we join the 4th point i. e. A4 with the line AB such that the line A4P is parallel to line A11B.
8. P is the required point, the point that divides the line in ratio of 4 : 7.
Length of AP = 2. 4cm (approximately )
Length of PB = 4. 1cm (approximately )
AP+PB = 2. 4+4. 1 = 6. 5 = AB.
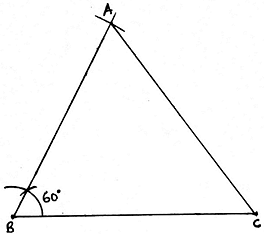
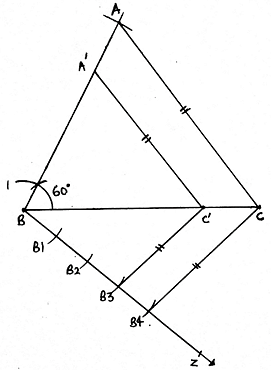
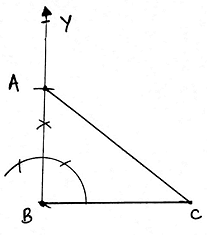
Q.3. Construct a ΔABC in which BC = 6. 5 cm, AB = 4. 5 cm and ∠ABC = 60°. Construct a triangle similar to this triangle whose sides are 3/4 of the corresponding sides of ∠ABC.
Steps of Construction:
1. First we draw a triangle ABC of given dimensions.
2. Draw a line segment BC of length 6. 5 cm.
3. From B, make an angle of 60° and draw a ray from B.
4. Now taking B as center and radius of 4. 5 cm (length of AB), draw an arc on the ray. The point is A.
5. Join AC.
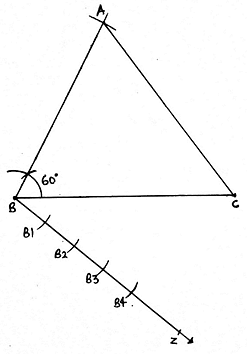
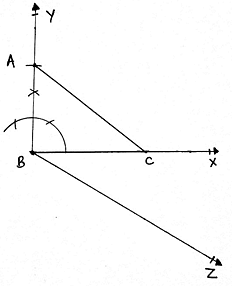
6. Now we have to make a triangle which is 3/4 times of this triangle.
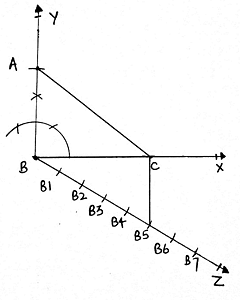
7. Draw a ray BZ making an acute angle with the line BC. Make 4 equal arcs starting from B then B1 and so on till B4.
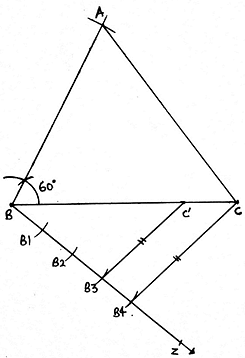
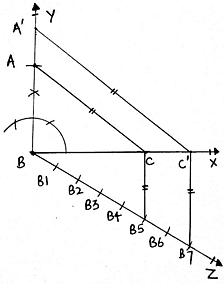
8. Join B4C. Draw a line from B3 parallel to B4C cutting BC at C’.
9. Draw another line from C’ parallel to CA cutting AB at A’.
10. A’BC’ is our required triangle.
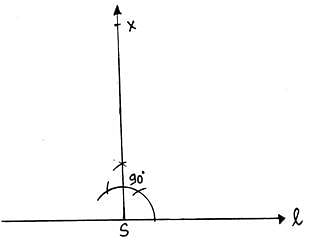
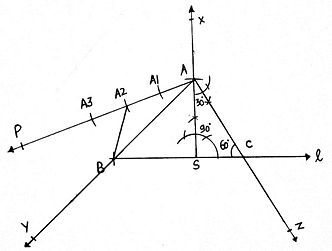
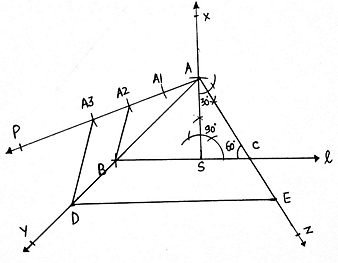
Q.4. Construct a ΔABC in which BC = 5 cm, ∠C = 60° and altitude from A equal to 3 cm. Construct a ΔADE similar to ΔABC such that each side of ΔADE is 3/2 times the corresponding side of ΔABC. Write the steps of construction.
Steps of Construction:
1. First we have to draw triangle of the given dimensions.
2. Draw a line l.
3. Take any point S on this line, and draw an angle of 90° from this point.
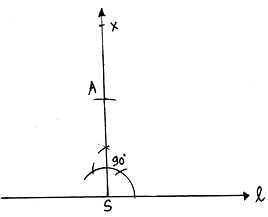
4. From S, draw an arc of length 3cm(length of altitude) cutting the perpendicular at A.
5. From A draw an angle of 30°, which cuts line l at C.
6. From C, draw an arc of length 5cm( length of BC) cutting line l at B.
7. Join AB. Then ABC is the triangle of given dimensions.
8. Draw a ray AP making an acute angle with the line AB.
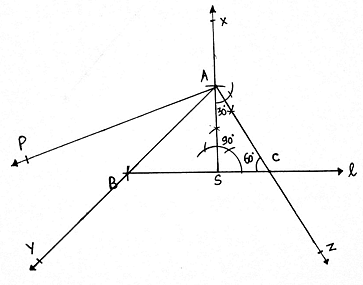
9. As we have to make a triangle ADE which is 3/2 times of this triangle, i. e. a bigger triangle. We extend AB to Y and AC to Z.
10. With A as center draw an arc on the ray AP. Then A1 as center and same radius draw another arc till we get A3.
11. Join A2B.
12. From A3 draw a line parallel to A2B cutting the AY at D.
13. From D, draw a line parallel to BC, cutting AZ at E.
14. Then ADE is the required triangle.
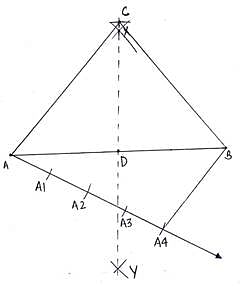
Q.5. Construct an isosceles triangle whose base is 9 cm and altitude 5 cm. Construct another triangle whose sides are 3/4 of the corresponding sides of the first isosceles triangle.
Steps of Construction:
1. Draw a line segment AB of length 9 cm.
2. Now as we know that the altitude of the isosceles triangle is also the bisector of the base line. So we draw a perpendicular bisector of line BC.
3. We cut an arc of length 5 cm( length of altitude). The arc cut point is C.
4. Join AB and AC. ABC is the triangle of the given dimensions.
5. Now we have draw a triangle which is 3/4 times of this triangle.
6. Draw a ray from A making an acute angle with AB. Make 4 equal arcs along the ray, i. e. A1, A2, A3, and A4.
7. Join A4B.
8. From A3, draw a line parallel to A4B cutting AB at B’.
9. From B’, draw another line parallel to BC cutting AC at C’.
10. AB’C’ is our required triangle.
Q.6. Draw a ΔABC, right-angled at B such that AB = 3 cm and BC = 4 cm. Now, construct a triangle similar to ΔABC, each of whose sides is 7/5 times the corresponding side of ΔABC.
Steps of Construction:
1. First we have to draw a triangle of given dimensions.
2. Draw a line segment of length BC of length 4cm.
3. Make an angle of 90° at B.
4. cut an arc of radius 3 cm taking B as center on the ray BY. The arc cut point is A.
5. Join AC. ABC is the right angled triangle with the given dimensions.
6. Now we have to make a triangle which 7/5 times of this triangle, that is bigger than this triangle.
7. So we extend the line BC along C to X and BA along A to Y.
8. Draw a ray BZ making an acute angle with BC.
9. Make 7 equal arcs along BZ starting from B then B1 and so on till B7.
10. Join B5C.
11. From B7 draw a ray parallel to B5C cutting the BX at C’.
12. From C’, draw another ray parallel to CA cutting BY at A’.
13. Then A’BC’ is our required triangle.
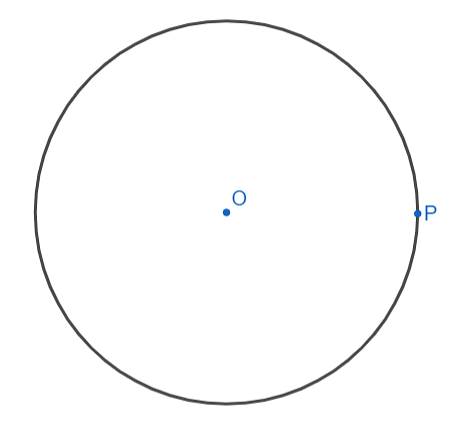
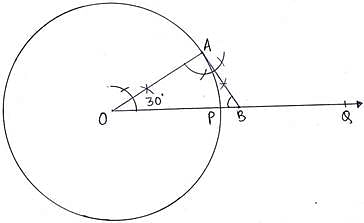
Q.7. Draw a circle of radius 4.8 cm. Take a point P on it. Without using the centre of the circle, construct a tangent at the point P. Write the steps of construction.
Steps of Construction:
1. Draw a circle of radius 4. 8 cm.
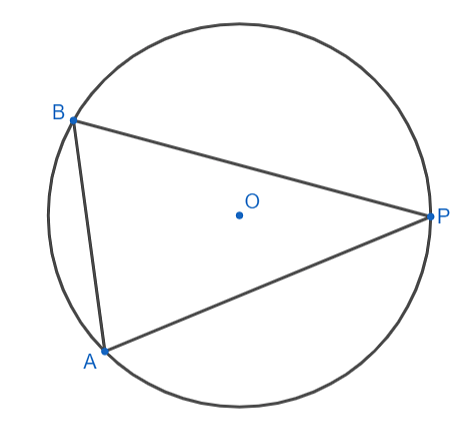
2. Take any point P on this circle. We have to draw tangent to this circle passing through P.
3. Draw any chord PA.
4. Take a point B in the major arc. Join BA and BP.
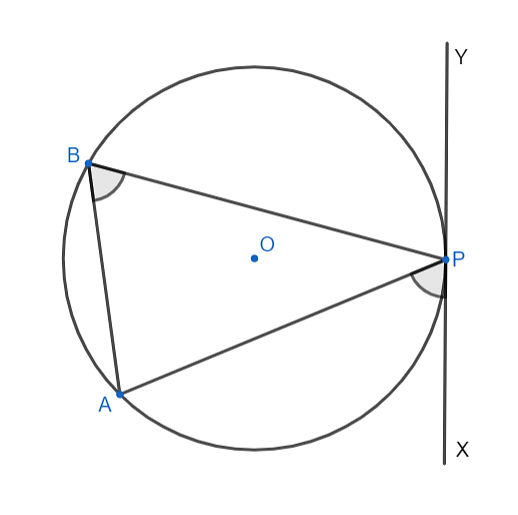
5. Draw angle ABP = angle APX.
6. Extend XP along P to Y.
7. then XY is the required tangent.
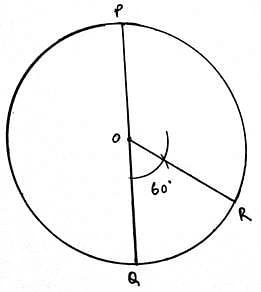
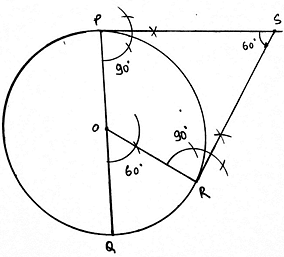
Q.8. Draw a circle of radius 3. 5 cm. Draw a pair of tangents to this circle which are inclined to each other at an angle of 60°. Write the steps of construction.
Steps of Construction:
1. Draw a circle with center O and radius of length 3. 5cm.
2. We then draw any diameter POQ of this circle.
3. We then draw an angle ROQ = 60°.
4. Draw angle of 90° from P and R.
5. Extend both the rays. The point where both the points intersect is S.
6. Then PS and RS are the required tangents.
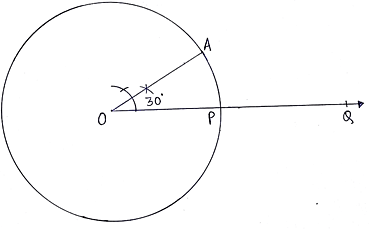
Q.9. Draw a circle of radius 4 cm. Draw tangent to the circle making an angle of 60° with a line passing through the centre.
Steps of Construction:
1. Draw a circle with center O and radius of length 4cm.
2. Draw any radius OP of this circle.
3. Extend OP to Q.
4. Draw angle AOP = 30°.
5. From A, draw angle of 90°.
6. The two lines intersect each other at B.
7. Then BA is the required tangent as angle ABP = 60°
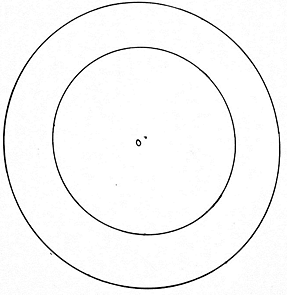
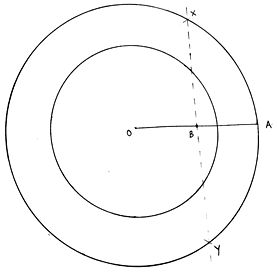
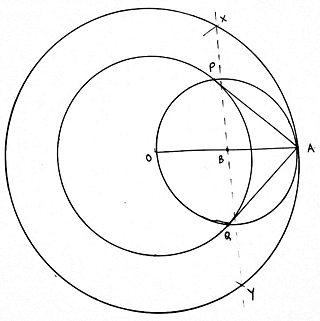
Q.10. Draw two concentric circles of radii 4 cm and 6 cm. Construct a tangent to the smaller circle from a point on the larger circle. Measure the length of this tangent.
Steps of Construction:
1. With O as a center, draw a circle of radius of 4cm and another circle of radius 6cm.
2. Mark any point A on the bigger circle.
3. Join OA. Draw perpendicular bisector of OA.
4. The perpendicular bisector XY of OA intersects OA at B.
5. With B as center and radius of length OB (or BA), draw a circle.
6. This circle intersects the smaller circle(of radius 4cm) at P and Q.
7. Join AP and AQ.
8. Then AP and AQ are the required tangents.
9. The measured length of AP and AQ is 4. 4cm (approximately).
|
53 docs|15 tests
|
|
53 docs|15 tests
|

|
Explore Courses for Class 10 exam
|

|