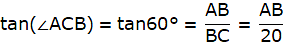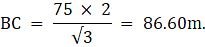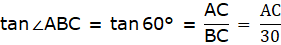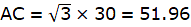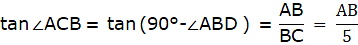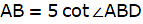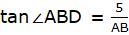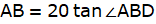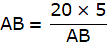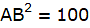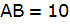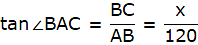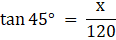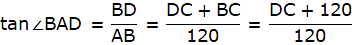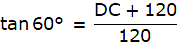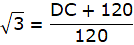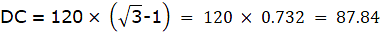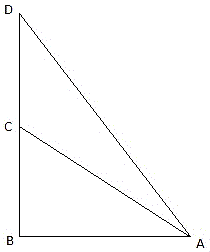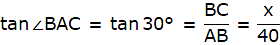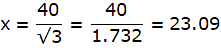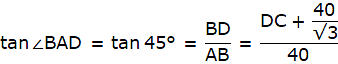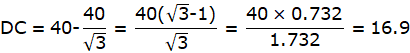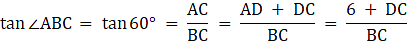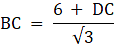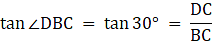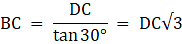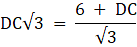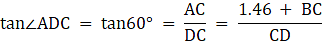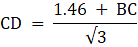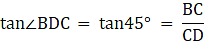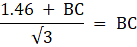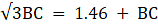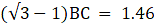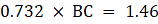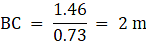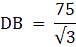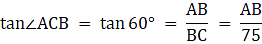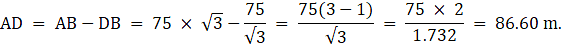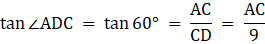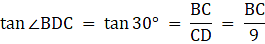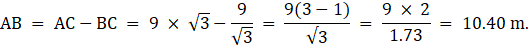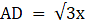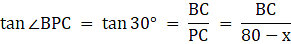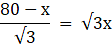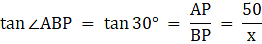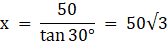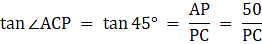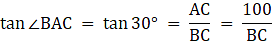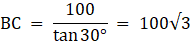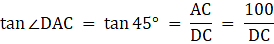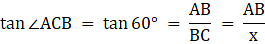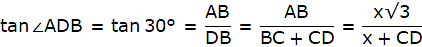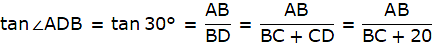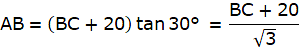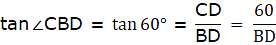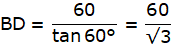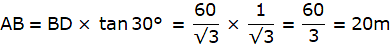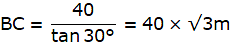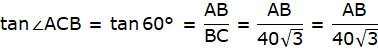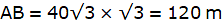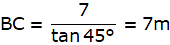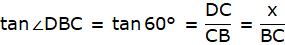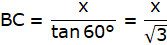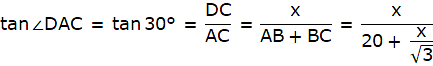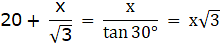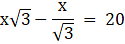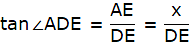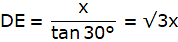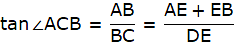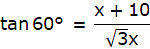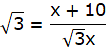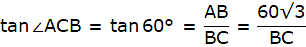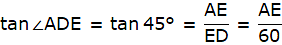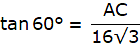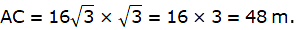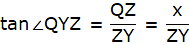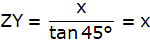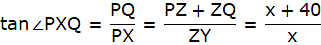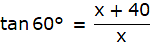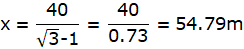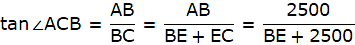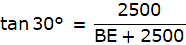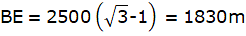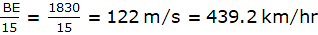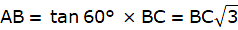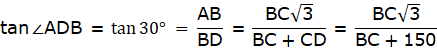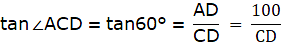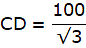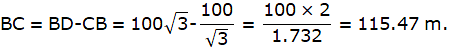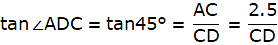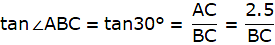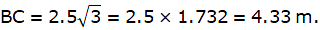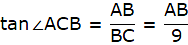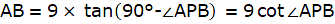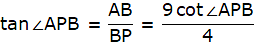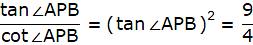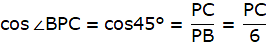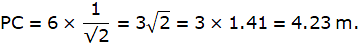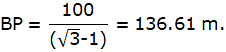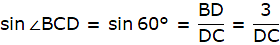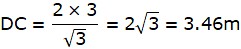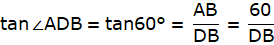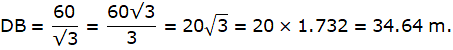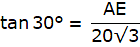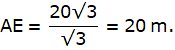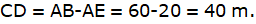RS Aggarwal Solutions: Heights and Distances- 1 | RS Aggarwal Solutions for Class 10 Mathematics PDF Download
Exercise: 14
Q.1. A tower stands vertically on the ground. From a point on the ground which is 20 m away from the foot of the tower, the angle of elevation of its top is found to be 60°. Find the height of the tower. [Take √3 = 1.732.]
Let AB be the tower and C be the point on the ground 20 m away from the foot of the tower B from where the angle of elevation of the top of the tower is 60°. Now, draw a line from C to A. Join B and C. We get a triangle ABC with right angle at B. We are to find the height of the tower, that is AB. We will be using trigonometric ratios involving AB(height) and BC(base). So, ∠ACB = 60° BC = 20m.
Now in ∆ABC,
or,
AB = 20√3 = 34.64m.
The height of the tower is 34.64 m.
Q.2. A kite is flying at a height of 75 m from the level ground, attached to a string inclined at 60° to the horizontal. Find the length of the string, assuming that there is no slack in it. [Take √3 = 1.732.]
Let A be the position of the kite in the sky. Let C be the position on the ground from where a string is attached to the kite. Since we have assumed that there is no slack in the string, we take AC to be a straight line making 60° angle with the ground. Draw a perpendicular from A on the ground which meets at point B. The kite is flying at a height of 75 m above the ground. So, AB = 75 m. Join B and C. We thus get a triangle ABC with right angle at B. We are to find the length of the string that is AC. We will use the trigonometric ratio sine which uses the perpendicular AB and the hypotenuse AC to find AC. Now, ∠ ACB = 60°
From ∆ABC,
or,
The length of the string is 86.60 m.
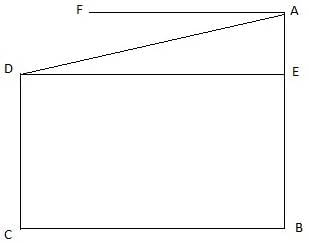
Q.3. An observer 1.5 m tall is 30 m away from a chimney. The angle of elevation of the top of the chimney from his eye is 60°. Find the height of the chimney.
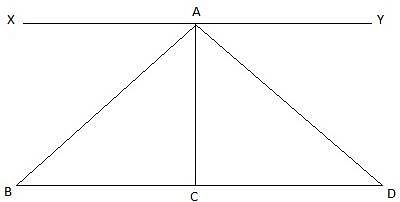
In the figure, let BD be the height of the man, i.e. BD = 1.5m. Let AE be the chimney in the figure. Join B and C. We get a triangle which is right angled at C. Clearly, BD = CE. Also, given that ∠ ABC = 60°. We use the trigonometric ratio tan which uses AC as height and BC as a base to find the height of the chimney AE.
Now, clearly CE = 1.5m. The height of the chimney is AE.
From ∆ABC,
or,
Thus, AC = 51.96m and CE = 1.5m. The height of the chimney AE = AC + CE = 51.96 + 1.5 = 53.46 m.
Hence, the answer is 53.46 m.
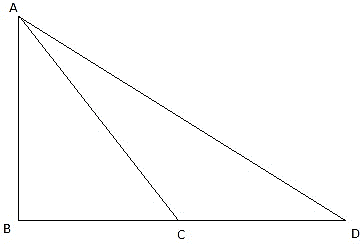
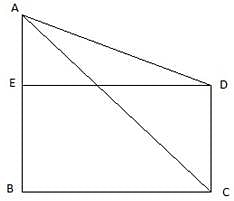
Q.4. The angles of elevation of the top of a tower from two points at distances of 5 meters and 20 meters from the base of the tower and in the same straight line with it are complementary. Find the height of the tower.
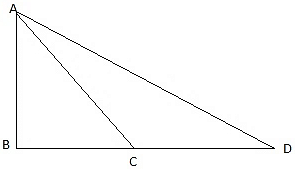
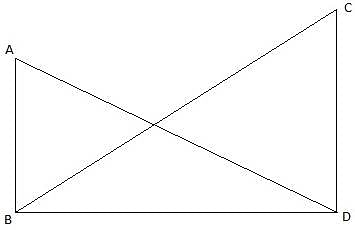
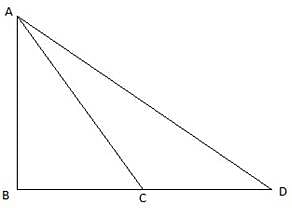
Let AB be the tower in the figure and C and D be two points on the straight line BD, at distances 5m and 20m from the foot of the tower AB. Now, join B, C, and C, D. We get two right-angled triangles both right angled at B. We use the trigonometric ratio tan by using AB as height and BC as a base(for ∆ABC) and AB as height and BD as a base(for ∆ABD) to find the height of the tower AB. By the problem we have, ∠ACB + ∠ADB = 90°.
In ∆ABC, we have
or,
or,
Also, from ∆ABD,
or,
Putting the value of tan ∠ABD in the equation we get
or,
or,
a positive value is taken since the height of the tower can’t be negative.
The height of the tower AB = 10m.
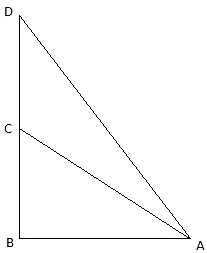
Q.5. The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45°. If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60°, then find the height of the flagstaff. [Use √3 = 1.732.]

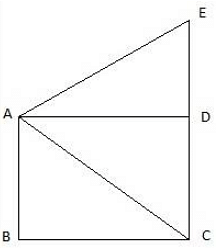
Let BC be the tower and CD be the flagstaff. Join C, A and D, A and A, B. We get two right-angled triangles ABC and BAD which are right-angled at B. By the problem, it is clear that ∠ BAC = 45° and ∠ BAD = 60°. We use trigonometric ratio tan for both the triangles using BC as height and AB as a base(for ∆ABC) and BD as height and AB as a base(for ∆ABD) to find the height of the flagstaff CD.
Let BC be x.
In ∆ABC we have,
or,
or,
x = 120
So, we get BC = 120m. In ∆ABD,
or,
or,
or,
So, height of the flagstaff = DC = 87.84m.
Q.6. From a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30°. The angle of elevation of the top of a water tank (on the top of the tower) is 45°. Find
(i) the height of the tower,
(ii) the depth of the tank.
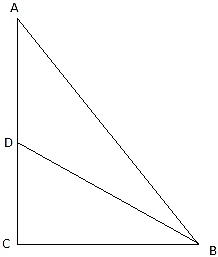
In the figure assume, A to be the point 40m away from the foot of the tower BC. Join A,B and A,C and A,D. Let DC be the water tank and BC be the tower. We get two right-angled triangles ABC and ABD, right angled at B. Also, ∠ BAC = 30° and ∠ BAD = 45°. We use trigonometric ratios tan using AB as base and BC as height(for ∆ABC) and AB as base and CD as height(for ∆ABD). Let BC be x.
In ∆ABC,
or,
So, BC = 23.09m.
In ∆ABD,
or,
i. Height of the tower = BC = 23.1m
ii. Depth of the tank = DC = 16.9m
Q.7. A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height 6 m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30° and that of the top of the flagstaff is 60°. Find the height of the tower. [Use √3 = 1 .732.]
Let AD be the Flagstaff, 6m high and DC be the tower. B be the point on the plane from where the angles of elevation of the top(A) and bottom of the flagstaff(D) are 60° and 30° respectively. Join C and B. Then we get two triangles ABC and BCD with right angle at C. We are to find the height of the tower DC. Now, to summarize, we are given, AD = 6m, ∠ ABC = 60°, and ∠ DBC = 30°. To find DC we will first find BC from the triangle ABC and again from triangle BCD and equate the expression for BC in both the cases. Then we will solve for DC from the equation.
In ∆ABC,
or,
In ∆BCD,
or,
Equating the values of BC,
or,
3DC = 6 + DC
or,
DC = 3m
Hence the height of the tower is 3m.
Q.8. A statue 1.46 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the top of the pedestal is 45° Find the height of the pedestal. [√3 = 1.73.]
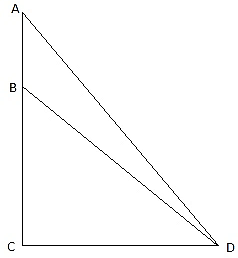
In the figure, let AB be the statue of height 1.46 m, BC the pedestal. Let D be a point on the ground from which the angles of elevation of the top of the statue and the top of the pedestal are 60° and 45° respectively. We are to find the height of the pedestal, which is BC. Join C and D. We get two triangles ACD and BCD with right angle at C. To find BC, we use trigonometric ratios to find the expression of CD from ACD and BCD and then equate them. Now, ∠BDC = 45°, ∠ADC = 60°, AB = 1.46 m.
From ∆ADC,
or,
Again, from ∆BCD,
or,
BC = CD
or,
or,
or,
or,
or,
Hence the answer is 2m.
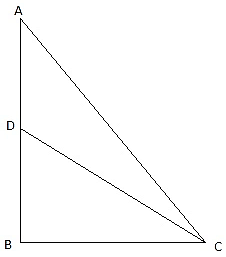
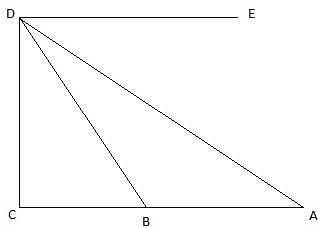
Q.9. The angle of elevation of the top of an unfinished tower at a distance of 75 m from its base is 30°. How much higher must the tower be raised so that the angle of elevation of its top at the same point may be 60°? [Take √3 = 1.732.]

In the above figure, let DB be the unfinished tower. Let C be the point on the ground, 75 m from the base B from which the angle of elevation of the top D is 30°. Let A be the point to which the tower must be raised such that the angle of elevation of it from C becomes 60°. Join B and C. We get two triangles ABC and BCD with right angle at B. We need to find the excess height that is an AD. We have, BC = 75 m, ∠BCD = 30° and ∠ACB = 60°. To find the AD, we will find AB and BD from the triangles ABC and BCD respectively using the trigonometric ratio tan and then subtract BD from AB.
Now, from ∆BCD,
or,
Again, from ∆ABC,
or,
AB = 75 x √3
Now, we have got both AB and DB. Then we are asked to find the AD.
Hence the answer is 86.6 m.
Q.10. On a horizontal plane, there is a vertical tower with a flagpole on the top of the tower. At a point, 9 meters away from the foot of the tower, the angle of elevation of the top and bottom of the flagpole is 60° and 30° respectively. Find the height of the tower and the flagpole mounted on it. [Take √3 = 1.73.]

In the above figure, let BC be the tower, AB is the flagpole. Let D be the point 9 m away from C such that the angle of elevations of the top and bottom of the flagpole AB are 60° and 30° respectively. Join C and D. We get two triangles ADC and BCD with right angle at C. We have to find the height of the tower BC and the height of the flagpole AB. For this, we use trigonometric ratio tan for triangles ACD and BCD to find AC and BC respectively. Subtract BC from AC to find AB.
Now we have, DC = 9 m, ∠ADC = 60°, and ∠BDC = 30°. We are to find AB and BC.
From ∆ACD,
or,
AC = 9 x √3
From ∆BDC,
or,
BC = 9/√3
Now,
And, BC = 9/1.73 = 5.20 m
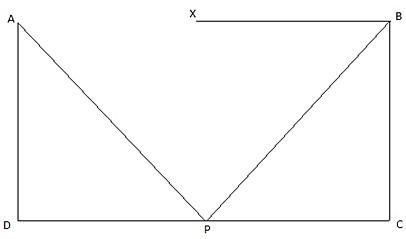
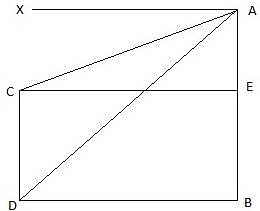
Q.11. Two poles of equal heights are standing opposite to each other on either side of the road which is 80 m wide. From a point P between them on the road, the angle of elevation of the top of one pole is 60° and the angle of depression from the top of another pole at P is 30°. Find the height of each pole and distances of the point P from the poles.

Let AD and BC be the two poles of equal height standing on the two sides of the road of width 80 m. Join DC. Then DC = 80 m. P is a point on the road from which the angle of elevation of the top of tower AD is 60°. Also, the angle of depression of the point P from the point B is 30°. Draw a line BX from B parallel to the ground. Then ∠XBP = ∠BPC = 30°. We are to find the height of the poles and the distance of the point P from both the poles. Also, ∠APD = 60°.
Let DP = x. Then PC = 80-x.
In ∆APD,
or,
Now, from ∆APD,
or,
Now, BC = AD
So,
or,
3x = 80 - x
or,
x = 20 m
So, PD = 20 m. Hence, PC = 80-20 = 60 m. Also, BC = AD = 20√3 m.
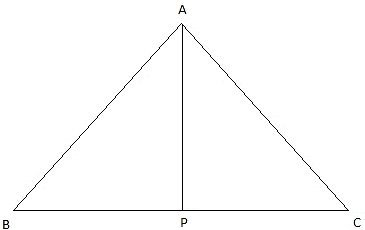
Q.12. Two men are on opposite sides of a tower. They measure the angles of elevation of the top of the tower as 30° and 45° respectively. If the height of the tower is 50 meters, find the distance between the two men. [Take √3 = 1.732.]
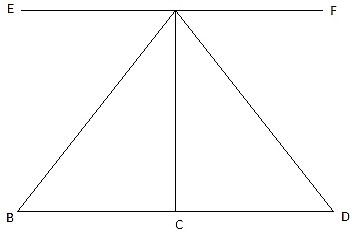
Let the positions of the two men are B and C. Let AP represent the tower in the figure. Join B, P, and C, P.We have, ∠ABP = 30° and ∠ACP = 45°. Given that AP = 50 m.We get two right-angled triangles ∆APB and ∆APC, both right angled at P. We use trigonometric ratio tan for both the triangles using BP as a base and AP as height(for ∆APB) and PC as base and AP as height(for ∆APC). We get BP and PC. The distance between the men is BC.
We have to find BC. Let BP = x. In ∆APB,
or,
Again, in ∆APC,
or,
PC = 50
So, distance between the two men is BC = BP + PC = 50√3 + 50 = 50(√3 + 1) = 136.6m.
Q.13. From the top of a tower 100 m high, a man observes two cars on the opposite sides of the tower with angles of depression 30° and 45° respectively. Find the distance between the cars. [Take √3 = 1.73.]
In the figure, let AC be the tower of height 100m. The angles of depression are ∠BAE and ∠DAF. Given, AC = 100m. Since the line EF is parallel to the line BD, we have ∠BAE = ∠BAC = 30°, ∠DAF = ∠DAC = 45°, where B, D are the positions of the cars. Join B, C, and C, D. We get two right-angled triangles ∆ABC and ∆ADC, both right angled at C. We use trigonometric ratio tan for both the triangles, where BC is the base and Ac is the height (for ∆ABC) and CD is the base and AC is the height in ∆ACD. We are to find the distance between the two cars, i.e. BD.
In ∆ABC,
or,
In ∆ADC,
or,
DC = 100
Therefore, the distance between the two cars is BD = BC + CD = 100√3 + 100 = 100(√3 + 1) = 273 m.
Q.14. A straight highway leads to the foot of a tower. A man standing on the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower form this point.
In the figure, let AB be the tower and D be the position of the car. Let C be the position of the car 6seconds later. The angles of depression are ∠DAE and ∠CAE. Join B, C, and C, D and A, E. Since AE is parallel to BD, we must have, ∠ADB = ∠DAE = 30°, ∠CAE = ∠ACB = 60°.
We get two right-angled triangles ∆ABC and ∆ABD, both right angled at B. We use trigonometric ratio tan for both the triangles using BC as base and AB as height for ∆ABC and BD as base and AB as height in ∆ABD. We find the CD.
Let BC = x.
In ∆ABC,
or,
AB = xtan60° = x√3
Again, in ∆ABD,
or,
CD = 2x
Now, the speed of the car = CD/6 = 2x/6 = x/3.
Hence, time taken by the car to reach the foot of the tower is = BC/(Speed of the car) = 3 secs.
Q.15. A TV tower stands vertically on a bank of the canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.
In the figure, let AB be the tower and BC be the canal. C is the point on the other side of the canal directly opposite the tower. Join B and C. Let D be another point, 20m away from C. Join C and D. We get two right-angled triangles ∆ABC and ∆ABD, both right angled at B. Given that, ∠ACB = 60° and ∠ADB = 30°. DC = 20m. We use trigonometric ratio tan using AB as height and BC as a base(for ∆ABC) and AB as height and BD as a base(for ∆ABD) to find AB and BC.
In ∆ABC,
tan ∠ACB = tan60° = AB/BC
or,
AB = BC x tan60° = BC√3
In ∆ABD,
or,
Equating the values of AB in ∆ABC and ∆ABD,
or,
3BC = BC + 20
or,
2BC = 20
or,
BC = 10
So, the width of the canal = BC = 10m. We found that AB = BC√3 = 10√3m.
So, height of the tower = AB = 10√3m.
Q.16. The angle of elevation of the top of a building from the foot of a tower is 30°. The angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
In the figure, let CD be the tower and AB be the building. Join the points A, D, and B, C. We get two right-angled triangles ∆ABD and ∆BCD, which are right-angled at B and D respectively. We are given that the angle of elevation of the top of the building from the foot of the tower is 30° and that of the top of the tower from the foot of the building is 60°. So, ∠CBD = 60°, ∠ADB = 30°. We are also given that the height of the tower is 60 m. Hence CD = 60 m. We need to find the height of the building, that is AB. For this, we will first find BD from ∆BDC using the trigonometric ratio tan. Using this value of BD, we will find the value of AB from ∆ABD using the trigonometric ratio tan.
In ∆BCD,
or,
So, BD = 60/√3m.
In ∆ABD,
or,
So, height of the building = AB = 20m.
Q.17. The horizontal distance between two towers is 60 metres. The angle of depression of the top of the first tower when seen from the top of the second tower is 30°. If the height of the second tower is 90 metres, find the height of the first tower. [Use √3 = 1.732.]
In the figure, let CD be the first tower and AB, the second tower. We are given that the distance between the two towers is 60 m. Join C and B. We thus get CB = 60 m. Again, we are given that the angle of depression of the top of the first tower from the top of the second tower is 30°. We draw a horizontal line parallel to BC from A to F. Then we get ∠FAD = 30°. Now, we draw a line from the top of the first tower onto the second tower parallel to BC to the point E. We get a right-angled triangle ADE with right angle at E. Then ∠ ADE = 30°.We are also given that the height of the second tower is 90 m. So, AB = 90m. We are told to find the height of the first tower, that is CD.
Note that, BC = ED = 60m.
To find CD, we use the trigonometric ratio tan on ∆ADE to find AE.
In ∆AED,
or,
AE = 60 x tan30° = 60/√3m
Now we just see that we can get the height of the first tower by subtracting the value of AE from AB to get BE which is equal to CD.
Height of the first tower = DC = AB-AE = 90-60/√3 = 55.35m.
Q.18. The angle of elevation of the top of a chimney from the foot of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30°. If the height of the tower is 40 metres, find the height of the chimney.
According to pollution control norms, the minimum height of a smoke-emitting chimney should be 100 metres. State if the height of the above-mentioned chimney meets the pollution norms. What value is discussed in this question?
Let AB be the chimney and DC be the tower. We are given that the angle of elevation of the top of the chimney from the foot of the tower DC is 60°. Join A and C. We get a right-angled ∆ABC with right angle at B and ∠ACB = 60°. We are again told that the angle of depression of the foot of the chimney from the top of the tower is 30°. If we join B and D, then we get a right-angled ∆BCD with right angle at C. Draw a line from D to a point on AB parallel to BC. So, ∠EDB = 30° and ∠DBC = 30°. The height of the tower is given to be 40 m. So, DC = 40m. We will first find the height of the chimney AB. If AB is less then 100 m, then it does not meet the pollution norms and if otherwise, then it does not meet the pollution norms.
First, we will find the value of BC from ∆BCD using the trigonometric ratio tan. Then using the value of BC, we will find the value of AB from ∆ABC using the trigonometric ratio tan.
In ∆BDC,
or,
In ∆ABC,
or,
So, the height of the chimney is AB = 120m, which is greater than 100 m.
The height satisfies the pollution norms.
Q.19. From the top of a 7-meter-high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. [Use √3 = 1.732.]
Let AB be the building and CE be the cable tower. We are given that, the angle of elevation of the top of the cable tower from the top of the building is 60° and the angle of depression of the bottom of the tower from the top of the building is 45°. Join C, E to A. Also draw a line from A to EC at the point D parallel to BC. We get two right-angled triangles ABC and AED with right angles at B and D respectively. Also, ∠EAD = 60°. ∠DAC = ∠ACB = 45°. Also given that the height of the building is 7 m. That is AB = 7m. We are to find the height of the tower CE.
We first find the value of BC from ∆ABC using the trigonometric ratio tan.
In ∆ABC,
or,
Now, AD = BC.
In ∆DAE,
or,
DE = 7 x tan60° = 7√3m
So, the height of the cable tower = CE = CD + DE = 7m + 7√3m = 19.12m.
Q.20. The angle of depression from the top of a tower of a point A on the ground is 30°. On moving a distance of 20 meters from the point A towards the foot of the tower to a point B, the angle of elevation of the top of the tower from the point B is 60°. Find the height of the tower and its distance from the point A.
Let DC be the tower. Given that the angle of depression of the point A on the ground from the top of the tower DC is 30°. Join C and A. Now draw a line DE parallel to CA. Also join A and D. Then, ∠ EDA = 30°. We get a right-angled triangle ACD with right angle at C and ∠DAC = 30°. If we move 20 m from A to B towards the foot of the tower C, then the angle of depression changes to 60°. Then, AB = 20 m. Join D and B. Then we get a right-angled triangle ∆DCB with right angle at C.
We are to find the height of the tower that is DC and its distance from A, that is, AC.
Let DC = x. In ∆DCB,
or,
In ∆ADC,
or,
or,
or,
x = 10√3 = 17.32 m
The height of the tower = DC = x = 17.32m.
We have, BC = x/√3 = 10m. So, a distance of A from the tower = AC = 20 + 10 = 30m.
Q.21. The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 30°. Find the height of the tower.

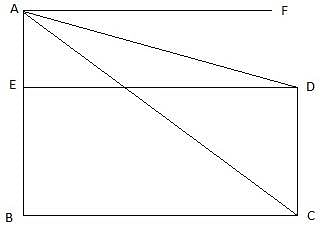
In the figure, let AB be the tower and C be the point on the ground from which the angle of elevation of the top of the tower AB is 60°. Join A and C and B and C. Then we get a right-angled triangle ABC with right angle at B and ∠ACB = 60°. Let D be the point 10 m vertically above C. Then, CD = 10 m. Given that the angle of elevation of the top of the tower from the point D is 30°. Join D and A. Also draw a line DE from D to AB, parallel to BC. Then we get a right-angled triangle AED with right angle at E and ∠ADE = 30°. We are to find the height of the tower, that is AB.
Clearly, ED = BC. Let AE = x
In ∆AED,
or,
tan30° = x/DE
or,
Again, in ∆ABC,
or,
or,
or,
3x = x + 10"
or,
x = 5m
Height of the tower = AB = AE + EB = 5m + 10m = 15m.
Q.22. The angles of depression of the top and bottom of a tower as seen from the top of a 60√3-m-high cliff are 45° and 60° respectively. Find the height of the tower.
Let AB be the cliff and CD be the tower. Join B and C. Draw a line AF parallel to BC. Now, given that the angles of depression of the top and bottom of the tower from the top of the cliff are 45° and 60° respectively. Hence, ∠FAD = 45° and ∠FAC = 60°. Draw a line DE from CD to AB parallel to BC. Also, join A, D and A, C. We get two right-angled triangles ADE and ABC with right angles at E and B respectively. Also, ∠ADE = ∠FAD = 45°, and ∠ACB = ∠FAC = 60°. We are also given that the height of the cliff AB is 60√3 m. We are to find the height of the tower, that is, CD.
We first find the value of BC from the ∆ABC, using the trigonometric ratio tan.
In ∆ABC,
or,
Clearly, ED = BC. Then, we will find the value of AE from ∆ADE using the trigonometric ratio tan. In ∆ADE,
or, AE = 60m.
The height of the tower = DC = 60√3m-60m = 43.92 m.
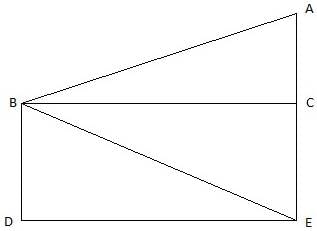
Q.23. A man on the deck of a ship, 16 m above water level, observes that the angles of elevation and depression respectively of the top and bottom of a cliff are 60° and 30°. Calculate the distance of the cliff from the ship and height of the cliff. [Take √3 = 1.732.]
In the above figure, let B be the position of the man and AE be the cliff. We are given that the position of the man is 16 m above water level. Draw a line BD to a point D on the water level. So, BD = 16 m. Now, we are given that the angle of elevation of the top of the tower from the position of the man is 60°. Join A and B. Also, draw a line BC on to the line AE parallel to the water level. Then we get a right angled triangle ABC with right angle at B and ∠ABC = 60°. Also, the angle of depression of the bottom of the tower from the position of the man is 30°. So, ∠CBE = 30°. Joining B and E we get a right angled triangle BDE. And, ∠BED = ∠CBE = 30°. We need to find the distance of the ship from the cliff, that is DE and the height of the cliff AE.
We first find DE from the ∆BDE by using the trigonometric ratio tan.
In ∆BDE,
tan ∠BED = BD/DE
or,
tan 30° = 16/DE
or,
DE = 16√3m = 27.71 m.
Now, BC = DE = 16√3 m.
From ∆ABC,
tan ∠ABC = AC/ BC
or,
or,
Also, CE = BD = 16 m.
Hence, the height of the cliff is AE = AC + CE = 48 + 16 = 64 m.
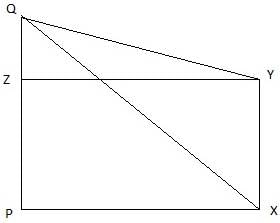
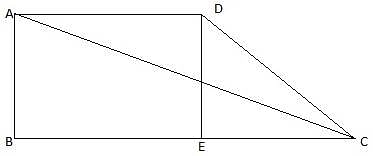
Q.24. The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation is 45°. Find the height of tower PQ. [Take √3 = 1.73.]
PQ is the tower and from a point X on the ground, the angle of elevation of the top of the tower is 60°. Join A and P, and Q and X. Then we get a right-angled triangle QPX with right angle at P and ∠QXP = 60°. Y is a point vertically above X. Then YX = 40 m. Draw a line YZ from Y onto the line QP parallel to PX. We are also given that the angle of elevation of the top of the tower from the point Y is 45°. Join Y and Q. We get a right-angled triangle QYZ with right angle at Z and ∠QYZ = 45°. We are to find the height of the tower PQ.
Clearly, ZY = XP, ZP = XY. Let QZ = x
In ∆QZY,
or,
tan 45° = x/ZY
or,
In ∆PQX,
or,
or,
√3x = x + 40
or,
QZ = ZY = x = 54.79 m.
The height of the tower PQ = PZ + ZQ = 54.79m + 40m = 94.79m.
Q.25. The angle of elevation of an aeroplane from a point on the ground is 45°. After flying for 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 2500 metres, find the speed of the aeroplane.
Let D be the initial position of the aeroplane, 2500 m above the ground. After 15 s, let A be the position of the aeroplane flying in the same height. Draw two lines AB and DE from A and D perpendicular to the ground. Then, AB = DE = 2500m. Let C be the point on the ground from which the angles of elevation of the two positions of the plane, viz., D and A are 45° and 30° respectively. Join A and D with C. Also join the points B,E and C on the ground. We then get two right-angled triangles ABC and DEC with right angles at B and E respectively. So, we get ∠ACB = 30° and ∠DCE = 45°. We are to find speed of the plane. The plane travels a distance AD in 15 s. Since speed = (distance/time), we need to find AD only.
We first find CE from ∆DEC using the trigonometric ratio tan θ.
In ∆DEC,
tan ∠DCE = DC/EC
or,
tan 45° = DE/EC
or,
DE = EC tan 45° = EC
or,
DE = EC = 2500 m.
Now, we will again use tan to find the value of BE from ∆ABC.
In ∆ABC,
or,
or,
or,
Now, BE = AD = 1830 m.
Speed of the aeroplane =.
Q.26. The angle of elevation of the top of a tower from a point on the same level as the foot of the tower is 30°. On advancing 150 m towards the foot of the tower, the angle of elevation becomes 60°. Show that the height of the tower is 129.9 metres. [Given √3 = 1.732]
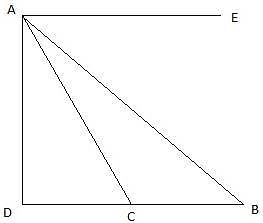
In the given figure, let AB be the tower. Let D be the point on the same level as the foot of the tower from which the angle of elevation of the top of the tower is 30°. Join B,C and A,D. Then we get a right-angled triangle ABD with right angle at B and ∠ADB = 30°. Let C be the point on the same level of the ground as Band D, 150 m from D towards B, from which the angle of elevation of the top of the tower is 60°. Joining A and C, we get a right angled triangle ABC, with right angle at B and ∠ACB = 60°. We are to show that the height of the tower AB is 129.9 m.
In ∆ABC,
tan ∠ACB = tan 60° = AB/BC
or,
In ∆ABD,
or,
3BC = BC + 150
So, BC = 75m. Now, AB = BC√3 = 75 × 1.732m = 129.9m. Hence proved.
Q.27. As observed from the top of a lighthouse, 100 m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° to 60°. Determine the distance travelled by the ship during the period of observation. [Use √3 = 1.732.]
In the above figure, let AD be the lighthouse and B and C be the two consecutive positions of the ship in view from it. The top of the lighthouse is 100 m above sea level. So, AD = 100 m. Also given that the angles of depression of the ship from the point A at the positions B and C are 30° and 60° respectively. Join D, C, B. Also join B, C to A. Then we get two right angled triangles ABD and ACD with right angles at D. Now, draw a line AE parallel to the sea level. Then, ∠EAB = ∠ABD = 30° and ∠EAC = ∠ACD = 60°. We are to find the distance travelled by the ship during the period of observation, that is, BC. We just use the trigonometric ratio tan from triangles ABD and ADC to find DB and DC respectively.
From ∆ACD,
or,
Again, from ∆ABD,
tan ∠ABD = AD/BD
or,
tan 30° = 100/BD
or,
BD = 100√3
Hence, distance travelled by ship during the observation is
Q.28. From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 2.5 m from the banks, find the width of the river. [Take √3 = 1.732.
In the above figure, let XY be the bridge and A be the point on the bridge from which two points, say B and D, on opposite sides of the river are observed. Join B and C. Given that the angles of depression of B and C from the point A are 30° and 45° respectively. Join B, D to A. So, ∠XAB = ∠ABD = 30° and also ∠YAD = ∠ADB = 45°. Again, draw a line AC from A perpendicular to the ground. Then, we get two right-angled triangles ABC and ACD with right angles at C. Now, given that the height of the bridge is AC = 2.5 m. We have to find the width of the river, that is BD.
From ∆ACD,
CD = 2.5m.
Again from ∆ABC,
or,
Hence, the width of the river is BD = BC + CD = 4.33 + 2.5 = 6.83m, which is the required solution.
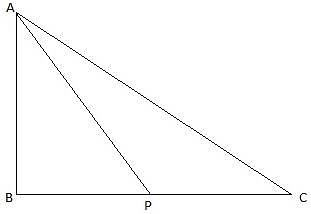
Q.29. The angles of elevation of the top of a tower from two points at distances of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Show that the height of the tower is 6 metres.

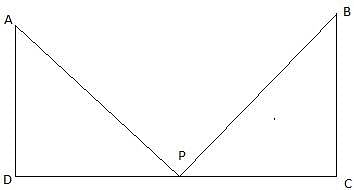
In the given figure, let AB be the tower. Let P and C be the points on the ground 4 m and 9 m from the foot of the tower. Join B, P and C. So, BC = 9m, BP = 4m. Again join P and C with A. Then we get two right-angled triangles ABP and ABC with right angle at B. Also, ∠APB and ∠ACB are given to be complementary. So, ∠APB + ∠ACB = 90°. We have to show that the height of the tower is 6 m.
We find the value of AB from ∆ABC using tan and also using the fact that tan(90-θ) = cotθ.
In ∆ABC,
or,
We will now use the above-found value of AB in ∆APB.
From ∆APB,
or,
or,
tan ∠APB = 3/2
or,
cot ∠APB = 2/3
Now, AB = 9 cot ∠APB = 9 x (2/3) = 3 x 2 = 6m.
Hence, proved.
Q.30. A ladder of length 6 metres makes an angle of 45° with the floor while leaning against one wall of a room. If the foot of the ladder is kept fixed on the floor and it is made to lean against the opposite wall of the room, it makes an angle of 60° with the floor. Find the distance between two walls of the room.

In the above figure, AD and BC are the two opposite walls of the same room. The ladder is fixed at the position say P on the floor. Join D,P and C. At first let it leans against the wall BC making an angle of 45° with the floor. Join B and P. We get a right-angled triangle BPC with right angle at C and ∠BPC = 45°. Again, when the ladder leans against the second wall AD, it makes an angle of 60° with the floor. Joining A and P, we get a right-angled triangle APD with right angle at D and ∠APD = 60°. We are to find the distance between the two walls, that is DC. Also given that, AP = PB = length of the ladder = 6 m.
To find DC, we separately find DP and PC from triangles APD and BPC respectively by using the trigonometric ratio cosine.
From ∆APD,
or,
DP = 1/2 x 6 = 3m.
Again, from ∆BPC,
or,
Hence, the distance between the two walls is, DC = DP + PC = 3 + 4.23 = 7.23m.
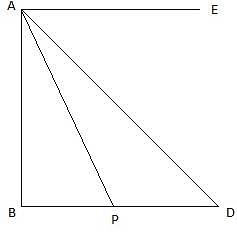
Q.31. From the top of a vertical tower, the angles of depression of two cars in the same straight line with the base of the tower, at an instant are found to be 45° and 60°. If the cars are 100 m apart and are on the same side of the tower, find the height of the tower.
In the above figure, let AB be the tower and P and D be the positions of the two cars at an instant, observed from A. join A and E. The angles of depression are ∠DAE and ∠PAE. Given that, PD = 100 m. Since AE is parallel to BD, so, ∠ADB = ∠DAE = 45° and ∠APB = ∠PAE = 60°. Join P,D and A,B. We get two right-angled triangles ∆ABD and ∆ABP. We are to find AB. We use trigonometric ratio tan for both the triangles, using AB as height and BP as base for ∆ABP and AB as height and BD as base for ∆ABD.
From ∆ABD,
tan ∠ADB = tan 45° = AB= BD
or, AB = BD
From ∆APB,
tan ∠APB = tan 60° = AB/BP
or, BD = BP√3
or, BP + 100 = BP√3
or, BP(√3-1) = 100
or,
Hence, the height of the tower is, AB = BD = BP + 100 = 136.61 + 100 = 236.61m
Q.32. An electrician has to repair an electric fault on a pole of height 4 metres. He needs to reach a point 1 metre below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use, which when inclined at an angle of 60° to the horizontal would enable him to reach the required position? [Use √3 = 1.73.]
Let AB be the pole and D be the 1m below A. The person needs to reach the point D. So, BD = 3m. Let DC be the ladder. Join D and C. We get a right-angled triangle ∆DBC, right angled at B. The angle of elevation of the ladder, ∠BCD = 60°. We use trigonometric ratio sin, using DC as hypotenuse and DB as height to find the length of the ladder DC.
In ∆BDC,
or,
Hence, the length of the ladder will be 3.46m.
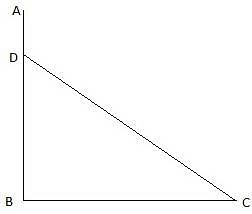
Q.33. From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
(i) the horizontal distance between AB and CD,
(ii) the height of the lamp post,
(iii) the difference between the heights of the building and the lamp post.
In the above figure, let AB be the building such that AB = 60 m. Join A and X. The angles of depression are ∠CAX = 30° and ∠DAX = 60°. Let CD be the lamp post. Join C,D and B,D and C,E. Since AX is parallel to DB, we must have ∠XAC = ∠ACE = 30° and ∠XAD = ∠ADB = 60°. We get two right-angled triangles ∆ABD and ∆CAE. We use trigonometric angle tan in both the triangles with AB as height and DB as base (for ∆ABD) and AE as height and CE as base(for ∆CAE).
We have to find, (i)BD, (ii)CD, and (iii) AB-CD.
From ∆ABD,
or,
DB = CE.
From ∆ACE,
tan ∠ACE = AE/CE
or,
or,
Hence,
And, the difference between the heights of the building and the lamp post is, AE = 20m.
Thus our solutions are,
(i) The horizontal distance between AB and CD = 34.64 m.
(ii) The height of the lamp post = 40 m.
(iii) Difference between the heights of the building and the lamp post = 20 m.
|
53 docs|15 tests
|
|
53 docs|15 tests
|

|
Explore Courses for Class 10 exam
|

|