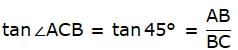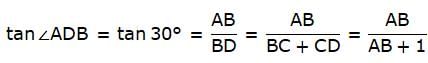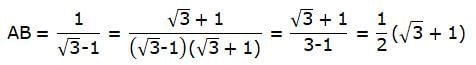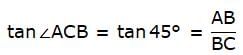Multiple Choice Questions (MCQ)
Question for RS Aggarwal Solutions: Heights and Distances- 2
Try yourself:If the height of a vertical pole is equal to the length of its shadow on the ground, the angle of elevation of the sun is
Explanation

In the figure let AB be the pole and BC is its shadow. Join A and C. We get a right-angled triangle ∆ABC. Angle of elevation of the sun is ∠ACB. Given that, AB = BC. We use trigonometric ratio tan taking AB as height and BC as base to find the angle ∠BCA.
In ∆ABC,
tan ∠ACB = AB/BC = 1
or,

since we know that tanθ is 1 whenever θ = 45°.
So, the correct option is (C).
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
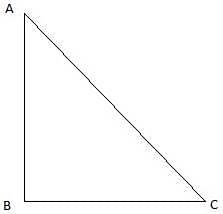
Try yourself:If the height of a vertical pole is √3 times the length of its shadow on the ground then the angle of elevation of the sun at that time is
Explanation

Let AB be the pole and BC be the shadow. Join A and C. We get a right-angled triangle right angled at B. The angle of elevation of the sun is ∠ ACB (= θ, say). We use the trigonometric ratio tan for the triangle taking AB as height and BC as the base. By the problem, AB = √3BC.
In ∆ABC,

or,
θ = 60°
since we know that tanθ is √3 whenever θ = 60°.
So, the correct option is (C).
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
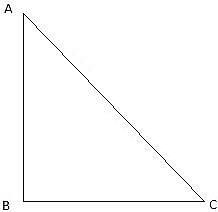
Try yourself:If the length of the shadow of a tower is √3 times its height then the angle of elevation of the sun is
Explanation

Let AB be the tower and BC be the shadow. Join A and C. We get a right-angled triangle right-angled at B. The angle of elevation of the sun is ∠ACB(θ, say). Given that, BC = √3AB. We will use trigonometric ratio tan for the triangle taking AB as height and BC as the base.
In ∆ABC,

or,
θ = 30°
since we know that tanθ is 1/√3 whenever θ = 30°.
So, the correct option is (B).
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
Try yourself:If a pole 12 m high casts a shadow 4√3 m long on the ground then the sun's elevation is
Explanation
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
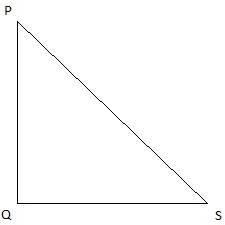
Try yourself:The shadow of a 5-m-long stick is 2 m long. At the same time, the length of the shadow of a 12.5-m-high tree is
Explanation
All we need to find is the angle of elevation of the sun. In the figure, AB is 5m long stick and BC is 2m long shadow of the stick. We join A and C to get a right-angled triangle ∆ABC. Angle of elevation of the sun is ∠ACB.

In ∆ABC,

or,
tan ∠ACB = 2.5

In this figure, PQ is the tree and QS is its shadow. ∠PSQ is the angle of elevation of the sun. So, ∠PSQ = ∠ACB. Join P and S. We get a right-angled triangle ∆PQS. Given, PQ = 12.5m. We use trigonometric ratio tan taking PQ as the height and QS as the base.
In ∆PQS,

or,

or,

So, the correct option is (D).
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
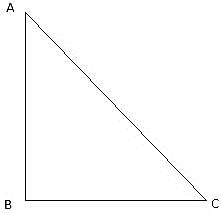
Try yourself:A ladder makes an angle of 60° with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, the length of the ladder is
Explanation
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
Try yourself:A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall then the height of the wall is
Explanation

In the figure, let AC be the ladder and AB is the wall. Join B and C. We get a right-angled triangle ∆ABC, right angled at B. Given, AC = 15m, ∠BAC = 60°. We use trigonometric ratio cos taking AC as the hypotenuse and AB as the base. In ∆ABC,

or,
AB = 15 x cos 60° = 15/2 m
So, the correct option is (C).
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
Try yourself:From a point on the ground, 30 m away from the foot of tower, the angle of elevation of the top of the tower is 30°. The height of the tower is
Explanation
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
Try yourself:The angle of depression of a car parked on the road from the top of a 150-m-high tower is 30°. The distance of the car from the tower is
Explanation
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
Try yourself:A kite is flying at a height of 30 m from the ground. The length of string from the kite to the ground is 60 m. Assuming that there is no slack in the string, the angle of elevation of the kite at the ground is
Explanation

Let the kite be at point A. Draw a line perpendicular to the ground at say point B. Since we are assuming no slack in the string, we can assume AC to be the string as in the figure. Join B and C to get a right-angled triangle ABC. Given that the kite is flying 30 m above the ground. So AC = 60 m. So, AB = 30 m. Also the length of the string is 60 m. We are to find the angle made by the string AC with the ground that is, ∠ACB.
In ∆ABC,

Since sin30° =1/2
∠ACB = 30°.
So, the correct option is (B).
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
Try yourself:From the top of a cliff 20 m high, the angle of elevation of the top of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is
Explanation

Let BD be the cliff and AE be the tower. Join D and E. Now, given that the angle of elevation of the top of the tower is same as the angle of depression of the foot of the tower as seen from the top of the cliff. Join A with B and E with B. Also draw a line BC from B onto AE parallel to DE. We get two right-angled triangles ABC and BDE with right angles at C and D respectively. The angle of elevation of the top of the tower AE from the point B is ∠ABC. And the angle of depression of the foot of the tower AE from the point B is ∠CBE which is same as ∠BED. Given, BD = 20m. We are to find the height of the tower, that is BD. Clearly, BD = CE = 20m, BC = DE. In ∆BCE,

or,

In ∆ABC,

or,
AC = 20m
So, height of the tower is AE = AC + CE = 20m + 20m = 40m
The correct option is (B).
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
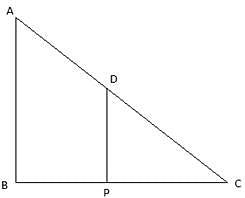
Try yourself:If a 1.5-m-tall girl stands at a distance of 3 m from a lamp post and casts a shadow of length 4.5 m on the ground, then the height of the lamp post is
Explanation

In the above figure, let PD be the girl, AB be the lamp post. Given that, the girl stands at a distance of 3 m from the lamp post. So BP = 3 m. Also the height of the girl is 1.5 m. So PD = 1.5 m. The shadow of the girl cast is of the length 4.5 m. So PC = 4.5 m. Then we have to find the height of the lamp post, that is, AB.
Now, BC = BP + PC = 3 + 3.5 = 7.5 m.
From ∆DPC,

∠ACB = ∠DCP. So, 
From, ∆ABC,

or,

or,

Hence the correct choice is C.
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
Try yourself:The length of the shadow of a tower standing on level ground is found to be 2x metres longer when the sun's elevation is 30° than when it was 45°. The height of the tower is
Explanation
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
Try yourself:The lengths of a vertical rod and its shadow are in the ratio 1: √3. The angle of elevation of the sun is
Explanation
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
Try yourself:A pole casts a shadow of length 2√3 m on the ground when the sun's elevation is 60°. The height of the pole is
Explanation
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
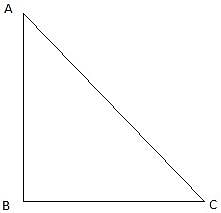
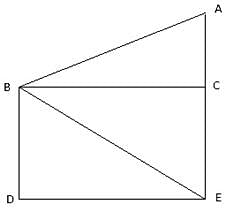
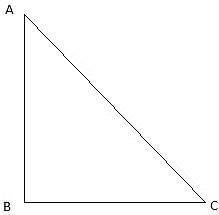
Try yourself:In the given figure, a tower AB is 20 m high and BC, its shadow on the ground is 20√3 m long. The sun's altitude is

Explanation
Given, AB = 20 m, its shadow BC = 20√3 m. We have to find ∠ACB.

So,
∠ACB = 30°
The correct choice is A.
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
Try yourself:The tops of two towers of heights x and y, standing on a level ground subtend angles of 30° and 60° respectively at the centre of the line joining their feet. Then, x : y is
Explanation

Let BC = x and AD = y be the two towers. They subtend angles 30° and 60° at the centre of the line joining their feet say P. Join C, P, D. Also join B, P and A, P. So, ∠BPC = 30° and ∠APD = 60°. Also, we get two right-angled triangles BPC and APD with right angles at C and D respectively. We have to find x:y.
From ∆BPC,
tan ∠BPC = BC/PC
or,

or,

From ∆APD,

or,

or,
y = PD√3
So, taking the ratio we get,

Hence, the correct choice is C.
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
Try yourself:The angle of elevation of the top of a tower from a point on the ground 30 m away from the foot of the tower is 30°. The height of the tower is
Explanation

In the above figure, let AB be the tower and C be the point on the ground 30 m away from the foot of AB from where the point A is observed. Join B, C and A, C. We get a right-angled triangle ABC with right angle at B. BC = 30 m. Also, the angle of elevation of the top of the tower AB from C is 30°. So, ∠ACB = 30°. We need to find the height of the tower, that is, AB.
In ∆ABC,

or,

or,

Hence the correct choice is B.
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
Try yourself:The string of a kite is 100 m long and it makes an angle of 60° with the horizontal. If there is no slack in the string, the height of the kite from the ground is
Explanation
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
Try yourself:If the angles of elevation of the top of a tower from two points at distances a and b from the base and in the same straight line with it are complementary then the height of the tower is
Explanation

In the above figure, let AB be the tower and C and D be the two points on the ground from where A is observed. Join B, C, D. Let BC = a and BD = b. Join C, D with A. We get two right-angled triangles ABC and ABD with right angle at B. Also, the angles of elevation of the top of the tower AB from C and D are ∠ACB and ∠ADB respectively. These angles are complementary. So,  We are to find the height of the tower, that is, AB.
We are to find the height of the tower, that is, AB.
From ∆ABD,

Again, from ∆ABC,

or,

or,

Now, multiplying we get,

or,
AB2 = ab
or,
AB = √ab
So the correct choice is (B).
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
Try yourself:On the level ground, the angle of elevation of a tower is 30°. On moving 20 m nearer, the angle of elevation is 60°. The height of the tower is
Explanation

Let AB be the tower and C, D are two points on the ground. Join B, C, D. Also, join A with C and D. We get two right-angled triangles ABC and ABD with right angle at B. The angles of elevation of the top of the tower from the points D and C are 30° and 60° respectively. So, ∠ADB = 30° and ∠ACB = 30°. We are to find the height of the tower. Also given that the distance from D to C is 20 m. So CD = 20 m.
In ∆ABC,

or,

In ∆ABD,

or,

or,

or,
AB = 10√3m
So, the correct option is (B).
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
Try yourself:In a rectangle, the angle between a diagonal and a side is 30° and the length of this diagonal is 8 cm. The area of the rectangle is
Explanation
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
Try yourself:From the top of a hill, the angles of depression of two consecutive km stones due east are found to be 30° and 45°. The height of the hill is
Explanation

Let AB be the hill and C, D are the km stones. Join B, C, D. Also join C, D with A. So we get two right-angled triangles ABC and ABD with right angle at B. Draw a line AE parallel to BD. Given that the angles of depression of C and D are 45° and 30° respectively. So, ∠EAD = ∠ADB = 30° and ∠EAC = ∠ACB = 45°. Now, CD = 1km. We are to find the height of the hill, that is, AB.
In ∆ABC,
or,
AB = BC
In ∆ABD,

or,

or,

So, the correct option is (B).
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
Try yourself:If the elevation of the sun changes from 30° to 60° then the difference between the lengths of shadows of a pole 15 m high, is
Explanation

Let AB be the pole and BD, BC is its shadows when the angle of elevation of the sun is 30°, 60° respectively. Here, the height of the pole is 15 m. So, AB = 15m. Join C and D with A. So we get two right-angled triangles ABC and ABD with right angle at B. And ∠ADB = 30° and ∠ACB = 60°. We are to find the difference between the length of the shadows, that is, CD. For this, we find the lengths BD and BC from triangles ABD and ABC respectively using the trigonometric ratio tan. In ∆ABC,

or,

In ∆ABD,

or,
CD = 15√3 -5√3 = 10 √3 m.
So, the correct option is (C).
Report a problem
Question for RS Aggarwal Solutions: Heights and Distances- 2
Try yourself:An observer 1.5 m tall is 28.5 m away from a tower and the angle of elevation of the top of the tower from the eye of the observer is 45°. The height of the tower is
Explanation

Let AE be the tower and CD be the observer. Join E and D. The observer is 28.5 m away from the tower. So, ED = 28.5 m. The observer is 1.5 m tall. So, CD = 1.5 m. Given that the angle of elevation of the top of the tower from the eye of the observer is 45°. Join A and C. Also draw a line BC from C onto AE parallel to DE. We get a right-angled triangle ABC with right angle at B and ∠ ACB = 45°. We are to find the height of the tower, that is, AE.
We see that, BC = ED = 28.5 m.
In ∆ABC,

or,
AB = BC = 28.5m
So, the height of the tower is AE = EB + BA = 1.5m + 28.5m = 30m.
The correct option is (B).
Report a problem


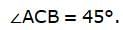
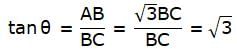
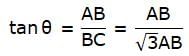
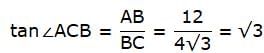
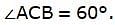
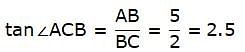


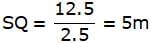


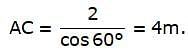

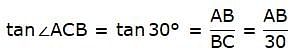
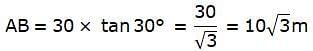


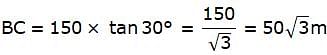
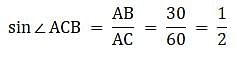

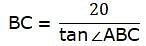
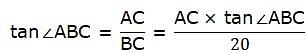
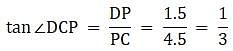
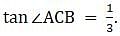
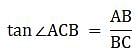

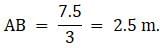
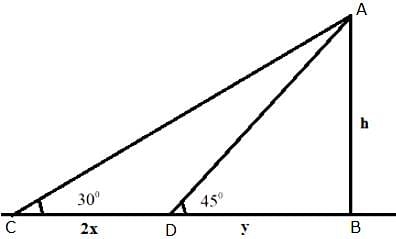
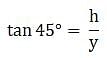
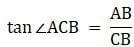
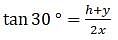
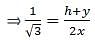
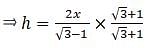
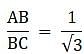


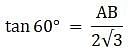
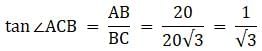


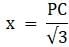



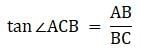




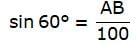


 We are to find the height of the tower, that is, AB.
We are to find the height of the tower, that is, AB.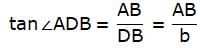


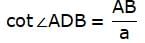


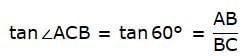

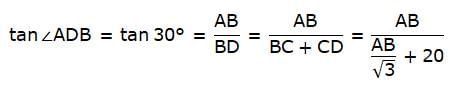





 .
.