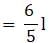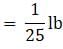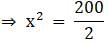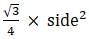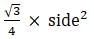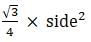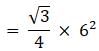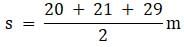Multiple Choice Questions (MCQ)
Question for RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 2
Try yourself:The length of a rectangular hall is 5 m more than its breadth. If the area of the hall is 750 m2 then its length is
Explanation
Given: Length of hall (l) = 5 + breadth(b) = 5 + b
Area of hall = 750 m2

We know that,
Area of rectangle = Length × Breadth
⇒ 750 = (5 + b) × b
⇒ 750 = b2 + 5b
⇒ b2 + 5b – 750 = 0
⇒ b2 + 30b – 25b – 750 = 0
⇒ b(b + 30) – 25(b + 30) = 0
⇒ (b + 30) (b – 25) = 0
This gives us two equations,
i. b + 30 = 0
⇒ b = -30
ii. b – 25 = 0
⇒ b = 25
Since, the length of the rectangle cannot be negative
Therefore, b = 25 m
⇒ l = (b + 5) m
⇒ l = (25 + 5) m
⇒ l = 30 m
Report a problem
Question for RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 2
Try yourself:The length of a rectangular field is 23 m more than its breadth. If the perimeter of the field is 206m, then its area is
Explanation
Given: Length of field (l) = 23 + breadth(b) = 23 + b
Perimeter of field = 206 m

We know that,
Perimeter = 2(l + b)
⇒ 206 = 2(23 + b + b)
⇒ 206 = 2(23 + 2b)
⇒ 206 = 46 + 4b
⇒ 4b = 206 – 46
⇒ 4b = 160
⇒ b = 40 m
Therefore,
Length of field = 23 + b
= 23 + 40
= 63 m
Now,
Area of rectangle = Length × Breadth
= 63 × 40
= 2520 m2
Report a problem
Question for RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 2
Try yourself:The length of a rectangular field is 12 m and the length of its diagonal is 15 m. The area of the field is
Explanation
Given:
Length = 12 m
Length of diagonal = 15 m

We know that,
Base2 + Perpendicular2 = Hypotenuse2
⇒ 122 + Perpendicular2 = 152
⇒ Perpendicular2 = 152 – 122
⇒ Perpendicular2 = 225– 144
⇒ Perpendicular2 = 81
⇒ Perpendicular2 = 9
That is,
Breadth = 9 m
Now,
Area = Length × Breadth
= 12 m × 9 m
= 108 m2
Report a problem
Question for RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 2
Try yourself:The length of a rectangle is thrice its breadth and the length of its diagonal is 8√10 cm. The perimeter of the rectangle is
Explanation
Given: Length of rectangle (l) = 3 × breadth(b) = 3b
Diagonal of rectangle = 8√10 m

We know that,
Base2 + Perpendicular2 = Hypotenuse2
⇒ b2 + (3b)2 = (8√10)2
⇒ b2 + 9b2 = 640
⇒ 10b2 = 640

⇒ b2 = 64
⇒ b = 8 cm
Therefore,
l = 3b = 24 cm
Hence,
Perimeter of a rectangle = 2(length + breadth)
= 2(24 + 8)
= 64 cm
Report a problem
Question for RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 2
Try yourself:On increasing the length of a rectangle by 20% and decreasing its breadth by 20%, what is the change in its area?
Explanation
Report a problem
Question for RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 2
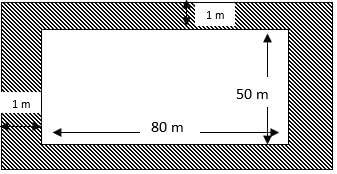
Try yourself:A rectangular ground 80 m x 50 m has a path 1 m wide outside around it. The area of the path is
Explanation
Given:
Length = 80 m
Breadth = 50 m
Width of the path = 1m
Area of path = 1911 m2

Length of field with path = 80 + (1 + 1)
= 82 m
Breadth of field with path = 50 + (1 + 1)
= 52 m
Area of field with path = Length of field with path × Breadth of field with path
= 82 m × 52 m
= 4264 m2
Area of field without path = Length without path × Breadth without path
= 80 m × 50 m
= 4000 m2
Now,
Area of path = Area of field - Area of field without path
= 4264 m2 – 4000 m2
= 264 m2
Report a problem
Question for RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 2
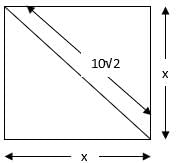
Try yourself:The length of the diagonal of a square is 10√2 cm. Its area is
Explanation
Given:
Length of diagonal = 10√2 cm
Let the side of square = x cm

We know that,
Hypotenuse2 = Base2 + Perpendicular2
⇒ (10√2)2 = x2 + x2
⇒ 200 = 2x2

⇒ x2 = 100
⇒ x = 10 cm
Now,
Area of a square = side2
= (10 cm)2
= 100 cm2
Report a problem
Question for RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 2
Try yourself:The area of a square field is 6050 m2. The length of its diagonal is
Explanation
Given:
Area of square field = 6050 m2
Let the side of square = x m

We know that,
Area of a square = side2
⇒ 6050 = x2
⇒ x = 55√2
Now,
Hypotenuse2 = Base2 + Perpendicular2
= (55√2)2 + (55√2)2
= 6050 + 6050
= 12100 m2
Therefore,
Diagonal = √12100
= 110 m
Report a problem
Question for RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 2
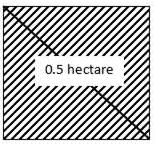
Try yourself:The area of a square field is 0.5 hectare. The length of its diagonal is
Explanation
Given:
Area of square field = 0.5 hectare = 5000 m2
Let the side of square = x m

We know that,
Area of a square = side2
⇒ 5000 = x2
⇒ x = 50√2
Now,
Hypotenuse2 = Base2 + Perpendicular2
= (50√2)2 + (50√2)2
= 5000 + 5000
= 10000 m2
Therefore,
Diagonal = √10000
= 100 m
Report a problem
Question for RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 2
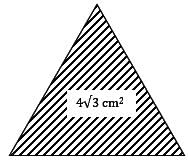
Try yourself:The area of an equilateral triangle is 4√3 cm2. Its perimeter is
Explanation
Report a problem
Question for RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 2
Try yourself:Each side of an equilateral triangle is 8 cm. Its area is
Explanation
Report a problem
Question for RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 2
Try yourself:Each side of an equilateral triangle is 6√3 cm. The altitude of the triangle is
Explanation
Report a problem
Question for RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 2
Try yourself:The height of an equilateral triangle is 3√3 cm . its area is
Explanation
Report a problem
Question for RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 2
Try yourself:The base and height of a triangle are in the ratio 3 : 4 and its area is 216 cm2. The height of the triangle is
Explanation
Given:
Base: Height = 3: 4
Area = 216 cm2
Let,
Base = 3x
Height = 4x

We know that,
Area of a triangle = 1/2 × base × height
⇒ 216 = 1/2 × 3x × 4x
⇒ 216 × 2 = 12x2
⇒ 12 x2 = 432

⇒ x2 = 36
⇒ x = 6 cm
Therefore,
Height = 4x
= 24 cm
Report a problem
Question for RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 2
Try yourself:The length of the sides of a triangular field are 20 m, 21 m and 29 m. The cost of cultivating the field at RS. 9 per m2 is
Explanation
Report a problem
Question for RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 2
Try yourself:The side of a square is equal to the side of an equilateral triangle. The ratio of their areas is
Explanation
Report a problem
Question for RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 2
Try yourself:The sides of an equilateral triangle is equal to the radius of a circle whose area is 154 cm2. The area of the triangle is
Explanation
Report a problem
Question for RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 2
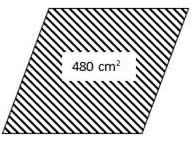
Try yourself:The area of a rhombus is 480 cm2 and the length of one of its diagonals is 20 cm. The length of each side of the rhombus is
Explanation
Given:
Area of rhombus = 480 cm2
Length of diagonal 1 (d1) = 20 cm

Let, Length of diagonal 2 be d2
Area of rhombus = 1/2 × d1 × d2
⇒ 480 = 1/2 × 20 × d2

⇒ d2 = 48 cm
Now,
Side of rhombus = 1/2 × √(482 + 202)
= 1/2 × √(2304 + 400)
= 1/2 × √2704
= 1/2 × 52
= 26 cm
Report a problem
Question for RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 2
Try yourself:One side of a rhombus is 20 cm long and one of its diagonals measures 24 cm. The area of the rhombus is
Explanation
Given:
Side = 24 cm
Length of diagonal 1 (d1) = 20 cm

Let, Length of diagonal 2 be d2
We know that,
Side of rhombus = 1/2 × √(d12 + d22)
⇒ 20 = 1/2 × √(242 + d22)
⇒ 20 × 2 = √(576 + d22)
⇒ 40 = √(576 + d22)
Squaring both sides,
⇒ 1600 = 576 + d22
⇒ d22 = 1024
⇒ d2 = 32 cm
Now,
Area of rhombus = 1/2 × d1 × d2
= 1/2 × 24 × 32
= 384 cm2
Report a problem
Question for RS Aggarwal Solutions: Perimeter and Area of Plane Figures- 2
Try yourself:The length of a rectangle is thrice its breadth and the length of its diagonal is 8√10 cm. The perimeter of the rectangle is
Explanation
Given: Length of rectangle (l) = 3 × breadth(b) = 3b
Diagonal of rectangle = 8√10 m

We know that,
Base2 + Perpendicular2 = Hypotenuse2
⇒ b2 + (3b)2 = (8√10)2
⇒ b2 + 9b2 = 640
⇒ 10b2 = 640

⇒ b2 = 64
⇒ b = 8 cm
Therefore,
l = 3b = 24 cm
Hence,
Perimeter of a rectangle = 2(length + breadth)
= 2(24 + 8)
= 64 cm
Report a problem