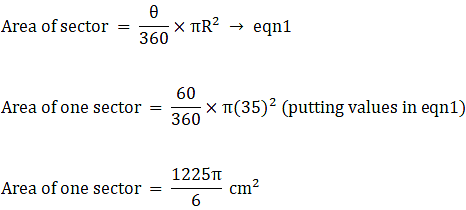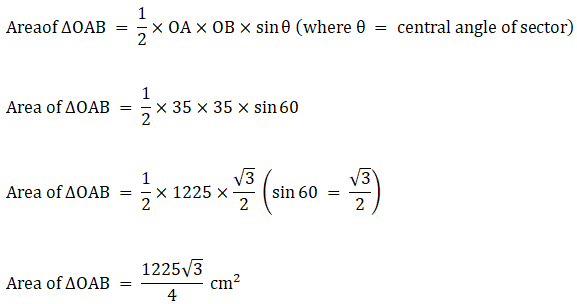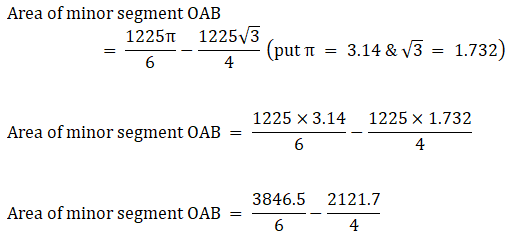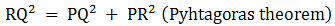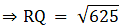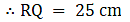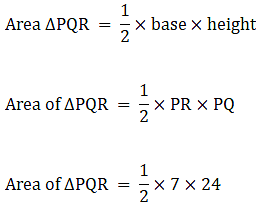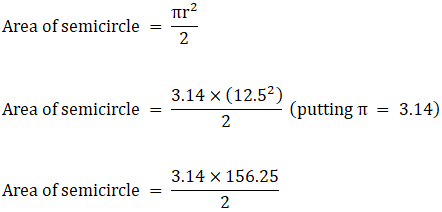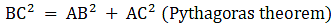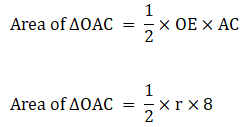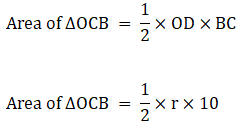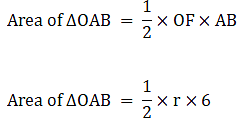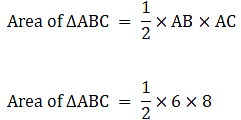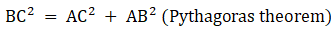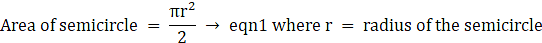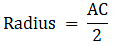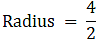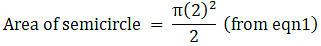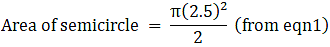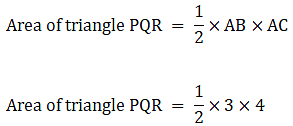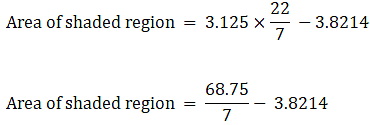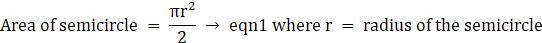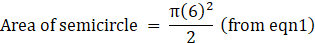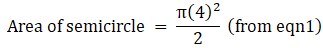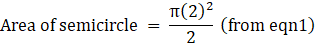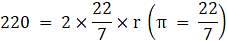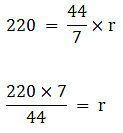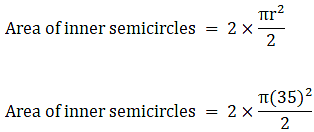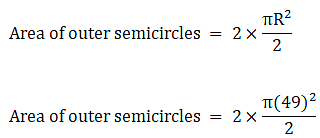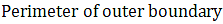RS Aggarwal Solutions: Area of Circle, Sector and Segment- 3 | RS Aggarwal Solutions for Class 10 Mathematics PDF Download
Q.41. In the given figure, ABCD is a trapezium of area 24.5 cm2. If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm, and ABE is quadrant of a circle then find the area of the shaded region.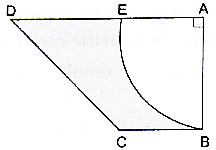
Here in order to find the area of the shaded region we have to calculate the area, or the quadrant shown and subtract it from the area of the trapezium. And in order to find the area of the quadrant we have to calculate the radius of the sector EAB by the area of trapezium.
Given Area of trapezium ABCD = 24.5 cm2 → eqn1
AD ∥ BC, AD = 10 cm, BC = 4 cm, ∠DAB = 90°
Putting the values in equation 2, we get,
⇒ AB = 3.5 cm
Therefore radius of the sector EAB = r = 3.5 cm
⇒ Area of the quadrant EAB = 9.625 cm2 → eqn3
∴ Area of shaded region = Area of trapezium – Area of quadrant EAB
⇒ Area of shaded region = 24.5 – 9.625 (putting values from eqn1 and eqn3)
⇒ Area of shaded region = 14.875 cm2
Q.42. ABCD is a field in the shape of a trapezium, AD || BC, ∠ABC = 90° and ∠ADC = 60°. Four sectors are formed with centres A, B, C and D, as shown in the figure. The radius of each sector is 14 m.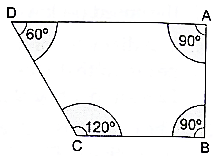
Find the following:
(i) total area of the four sectors,
(ii) area of the remaining portion, given that AD = 55 m, BC = 45 m and AB = 30 m.
Here in order to find the area of the shaded region we have to calculate the area, or the quadrant shown and subtract it from the area of the trapezium. And in order to find the area of the quadrant we have to calculate the radius of the sector EAB by the area of trapezium.
Given AB = 30 m, AD = 55 m, BC = 45 m
θA = 90°, θB = 90°, θC = 120°, θD = 60°
Radius of each sector = r = 14 m
(i) total area of 4 sectors
Area of sector at corner A = 49π m2→ eqn2
As we know that central angle at A and B are both 90 degrees and radius is also same i.e. 14 m therefore the area of the sector at B will be exactly same as that of sector at A.
∴ Area of sector at corner B = Area of sector at corner A
⇒ Area of sector at corner B = 49π → eqn3
Similarly,
Area of sector at corner C = 65.33π m2→ eqn4
Similarly,
Area of sector at corner D = 32.67π → eqn5
Total area of 4 sectors = eqn2 + eqn3 + eqn4 + eqn5
⇒ Total area of 4 sectors = 49π + 49π + 65.33π + 32.67π
⇒ Total area of 4 sectors = 196π
∴ Total area of 4 sectors = 616 m2
Total area of 4 sectors is 616 m2.
(ii) Area of the remaining portion
Here in order to find the area of the remaining portion of the trapezium we have to subtract the area of the 4 sectors from the area of the trapezium.
On putting the values,
Area of trapezium = 1/2 x (55 + 45) x 30
= 50×30
Area of trapezium = 1500 m2→ eqn1
Area of remaining portion = Area of trapezium – Area of the 4 sectors
⇒ Area of remaining portion = 1500 – 616 (from eqn1 and part (i))
∴ Area of remaining portion = 884 m2
The area of the remaining portion is 884 m2.
Q.43. Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex of an equilateral triangle of side 12 cm as centre and a sector of circle of radius 6 cm with centre B is made. [Use √3 = 1.73 and π = 3.14.]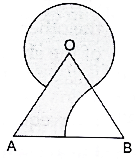
Area of shaded region can be calculated by subtracting the area of minor sector at vertex B from the sum of areas of the major sector at O and area of equilateral triangle.
Given Radius of circle at O = r = 6 cm
Side of equilateral triangle = a = 12 cm
Central angle at O = 360 -60 = 300°
Central angle at B = 60°
Area of the equilateral triangle =
where a = side of equilateral triangle
Area of the equilateral triangle =(putting the value of a)
Area of the equilateral triangle = (144×√3)/4
Area of the equilateral triangle = 36√3 cm2 → eqn1
Area of sector = θ/360×πR2 where r = radius of the sector
Area of minor sector at B = 60/360×π×(62) (given)
∴ Area of minor sector at B = 6π cm2→ eqn2
Similarly,
∴ Area of major sector at O = 30π cm2→ eqn3
Area of shaded region = eqn1 + eqn3 – eqn2
On putting values
⇒ Area of shaded region = 36√3 + 30π-6π
Area of shaded region = 36√3 + 24π
(put π = 3.14 and √3 = 1.73
∴ Area of shaded region = (36×1.73) + (24×3.14)
⇒ Area of shaded region = 62.28 + 75.36
∴ Area of shaded region = 137.64 cm2
Area of the shaded region is 137.64 cm2.
Q.44. In the given figure, ABCD is a rectangle with AB = 80 cm and BC = 70 cm, ∠AED = 90° and DE = 42 cm. A semicircle is drawn, taking BC as diameter. Find the area of the shaded region.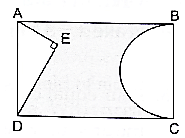
Here in order to find the area of the shaded region we have to subtract the area of the semicircle and the triangle from the area of the rectangle.
Given AB = 80 cm, BC = 70 cm, DE = 42 cm, ∠AED = 90°
Here we see that the triangle AED is right angle triangle, therefore, we can apply Pythagoras theorem i.e.
H2 = P2 + B2 (pythagoras theorem)
AD2 = DE2 + AE2
⇒ 702 = 422 + AE2 (putting the given values)
⇒ 4900 = 1764 + AE2
⇒ 4900 – 1764 = AE2
⇒ 3136 = AE2
AE = √3136
∴ AE = 56 cm
Area of ∆AED = 1/2×AE×DE
(Area of triangle = 1/2×base×height)
On putting values we get,
Area of ∆AED = 1/2×56×42
⇒ Area of ∆AED = 28×42
∴ Area of ∆AED = 1176 cm2→ eqn1
R = 35 cm
⇒ Area of semicircle = 11×175
∴ Area of semicircle = 1925 cm2→ eqn2
Area of rectangle = ℓ×b (ℓ = length of rectangle, b = breadth of rectangle)
⇒ Area of rectangle = 80×70 = 5600 cm2→ eqn3
Area of shaded region = Area of rectangle – Area of semicircle – Area of ∆
⇒ Area of shaded region = 5600 -1925 – 1176 (fromeqn1, eqn2 and eqn3)
∴ Area of shaded region = 2499 cm2
Area of the shaded region is 2499 cm2.
Q.45. In the given figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside the region. Find the area of the shaded region. [Use π = 3.14.]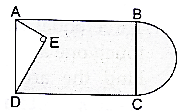
Here in order to find the area of the shaded region (region excluding the triangle) we have to subtract the area of the triangle from the area of the rectangle and then add the area of the semicircle.
Given AB = 20 cm, DE = 12 cm, AE = 9 cm and ∠AED = 90°
Here we see that the triangle AED is right angle triangle, therefore, we can apply Pythagoras theorem i.e.
AD2 = DE2 + AE2
AD2 = 122 + 92 (putting given values)
⇒ AD2 = 144 + 81
⇒ AD2 = 225
⇒ AD = √225
∴ AD = 15 cm
Area of ∆AED = 1/2×AE×DE
(Area of triangle = 1/2×base×height)
On putting values we get,
⇒ Area of ∆AED = 9×6
∴ Area of ∆AED = 54 cm2→ eqn1
Here radius of semicircle = BC/2 = 15/2
⇒ R = 7.5 cm
⇒ Area of semicircle = 1.07×56.25
∴ Area of semicircle = 88.3125 cm2→ eqn2
Area of rectangle = ℓ×b
(ℓ = length of rectangle, b = breadth of rectangle)
⇒ Area of rectangle = 20×15
(putting the values of ℓ & b)
∴ Area of rectangle = 300 cm2→ eqn3
Area of shaded region = Area of rectangle + Area of semicircle – Area of ∆
⇒ Area of shaded region = 300 + 88.3125 – 53 (from eqn1, eqn2, eqn3)
∴ Area of shaded region = 334.3125 cm2
Area of shaded region is 334.3125 cm2.
Q.46. In the given figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of shaded region. [Use π = 3.14.]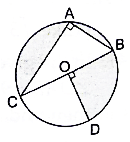
Here in order to find the area of the shaded region (region excluding the area of segment AC and quadrant OCD) can be calculated by subtracting the area of triangle and quadrant OBD from the area of the circle.
Given AC = 24 cm, AB = 7 cm and ∠BOD = 90°
Here we see that the triangle ACB is right angle triangle, therefore, we can apply Pythagoras theorem i.e.
BC2 = AC2 + AB2
⇒ BC2 = 242 + 72 (putting the given values)
⇒ BC2 = 576 + 49
⇒ BC2 = 625
BC = √625
∴ BC = 25 cm
Area of ∆ACB = 1/2×AB×AC (Area of triangle = 1/2×base×height)
On putting values we get,
⇒ Area of ∆AED = 7×12
∴ Area of ∆AED = 84 cm2→ eqn1
Area of circle = πR2 (R = radius of circle)
⇒ R = 12.5 cm
∴ Area of circle = π× 12.52
⇒ Area of circle = 156.25×3.14 (put π = 3.14)
∴ Are of circle = 490.625 cm2→ eqn2
⇒ Area of quadrant OBD = 122.65625 cm2→ eqn3
Area of shaded region = Area of circle – Area of quadrant – Area of ∆
⇒ Area of shaded region = 490.625 – 84 – 122.65625 (from eqn1, 2 and 3)
⇒ Area of shaded region = 283.96875 cm2
Area of shaded region is 283.96875 cm2.
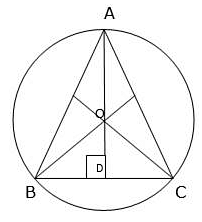
Q.47. In the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region. [Use √3 = 1.73 and π = 3.14.]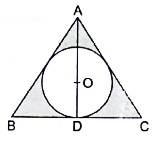
Here we will draw median from all the vertices of the equilateral triangle and the point at which they intersect will be the incircle of the triangle and that will be the centre of the circle. Thenwith the help of which we will find out the height of the triangle and subsequently the radius of the circle and ultimately the area of the shaded region (region of equilateral triangle excluding the area of circle inscribed).
As AD = BF = CE = h
Consider ∆ADB, ∠ADB = 90°, BD = 6 cm
122 = AD2 + 62 (putting the given values)
144 = AD2 + 36
144 – 36 = AD2
AD2 = 108
We also know that a point O will divide each median in a ratio of 2:1
Area of the circle = πr2
∴ Area of the circle = 12π cm2→ eqn1
Area of shaded region = area of triangle – area of circle
⇒ Area of the shaded region = (36×1.73) – (12×3.14)
⇒ Area of the shaded region = 62.28 -37.68
∴ Area of the shaded region = 24.6 cm2
Q.48. On a circular table cover of radius 42 cm, a design is formed by a girl leaving an equilateral triangle ABC in the middle, as shown in the figure. Find the covered area of the design. [Use √3 = 1.73]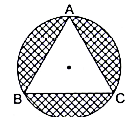
Here we will first find the sides of equilateral triangle ant then subtract the area of the triangle from the area of the circle.
Given radius of circle = r = 42 cm
∴ Area of the circle = πR2, where R = radius of the circle
⇒ Area of the circle = π(422)
⇒ Area of the circle = 22×252
∴ Area of the circle = 5544 cm2→ eqn1
Consider the figure shown,
In ∆ABD, ∠ADB = 90°
Let the sides of the equilateral triangle = a cm
And as we know AD is a median therefore it will bisect the side BC into two equal parts i.e.
BD = DC → eqn3
Also, BC = BD + DC
⇒ BC = BD + BD (from eqn3)
⇒ a = 2BD (BC = a)
BD= a/2 cm
Now, we also know that the point ‘O’ which is the intersection of all the three medians i.e. centroid of the triangle. Also we know that the centroid divides the median in the ratio 2:1.
Also, we know AO = radius = r = 42 cm
⇒ AD = 63 cm
Putting the value in equation 4,
Area of covered by design = Area of circle – Area of triangle ABC
⇒ Area covered by design = 5544 – 2288.79
∴ Area covered by design = 3255.21 cm2
Area covered by design is 3255.21 cm2.
Q.49. The perimeter of the quadrant of a circle is 25 cm. Find its area.
We know perimeter of a sector = Length of its arc + 2R → eqn1
Where R = radius of the sector.
Perimeter = 25 cm
θ = 90°
⇒ R = 7 cm → eqn2
∴ Area of the quadrant = 38.5 cm2
Area of the quadrant is 38.5 cm2.
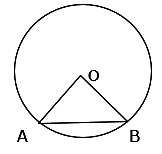
Q.50. A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]
Given the radius of the circle = 42 cm
Central angle of the sector = θ = 90°
Area of the minor segment = Area of sector – area of the right angle triangle
⇒ Area of the sector = 25×3.14
∴ Area of the sector = 78.5 cm2→ eqn1
∴ Area of triangle = 50 cm2→ eqn2
Area of the minor segment = 78.5 – 50 (from eqn1, eqn2)
∴ Area of the minor segment = 28.5 cm2
Area of the minor segment is 28.5 cm2.
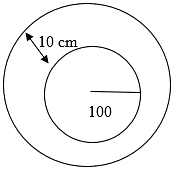
Q.51. The radius of a circular garden is 100 m. There is a road 10 m wide, running all around it. Find the area of the road and the cost of levelling it at Rs. 20 per m2. [Use π = 3.14.]
Here we will first find out the area of the road running around the circular garden and then multiplying it with rate per square meter to calculate the cost of leveling.
Here we see in the figure there are two concentric circles so,
Area of road = Area of outer circle- Area of circular garden
Area of circle = πR2 (where R = radius of circle) → eqn1
Let the radius of inner circle = r = 100 m
Also, radius of outer circle = R = 110 m (R = r + 10)
Area of outer circle = π(110)2→ eqn2 (putting R in eqn1)
Area of inner circle = π(100)2→ eqn2 (putting r in eqn1)
∴ Area of road = π(110)2 – π(100)2 (from eqn2 and 3)
⇒ Area of road = π(12100 – 10000)
⇒ Area of road = 2100 π (put π = 3.14)
⇒ Area of road = 2100×3.14
∴ Area of road = 6594 m2
Cost of leveling = Rate of leveling × Area of road
⇒ Cost of leveling = 20×6594
∴ Cost of leveling = Rs.131880
Area of road is 6594 m2 and cost of leveling is Rs.131880.
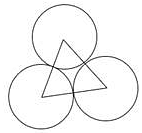
Q.52. The area of an equilateral triangle is 49√3 cm2. Taking each angular point as centre, circles are drawn with radius equal to half the length of the side of the triangle. Find the area of the triangle not included in the circles. [Take √3 = 1.73.]
Each angle of triangle = θ = 60°
Area of triangle not included in circles = Area of triangle – Area of all sectors
Area of all 3 sectors area equal as all the three circles are having same radius which is equal to the half of the side of the equilateral triangle.
Let the side of equilateral triangle be = a cm
⇒ a = 7×2
⇒ a = 14 cm
So radius of the circles = 7 cm
∴ Area of all 3 sectors = 77 cm2→ eqn1
Area of triangle not included = (49×1.73) - 77
⇒ Area of triangle not included = 84.77 – 77
∴ Area of triangle not included = 7.77 cm2
Area of triangle not included in circles is 7.77 cm2.
Q.53. A child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, BP ⊥ CD, HQ ⊥ FI and EL ⊥ DF. If CD = 8 cm, BP = HQ = 4 cm and DE = EF = 5 cm, find the area of the whole figure. [Take π = 3.14.]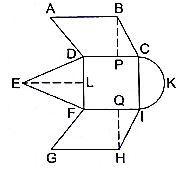
Area of whole figure = ar || ABCD + ar || FGHI + ar DCIF + ar ∆DEF + area semicircle
CD = 8 cm, BP = HQ = 4 cm, DE = EF = 5 cm, CI = 8 cm
ar ∥ ABCD = ar ∥ FGHI = base × height
ar ∥ ABCD = ar ∥ FGHI = BP×DC
ar ∥ ABCD = ar ∥ FGHI = 4×8
ar ∥ ABCD = ar ∥ FGHI = 32 cm2→ eqn1 and eqn2
ar DCIF = area of square = side×side
ar DCIF = DC×CI
ar DCIF = 8×8
ar DCIF = 64 cm2→ eqn3
Consider ∆DEF, EF⊥DF and ∆DEF is isosceles
So, FL = LD
FL = LD = 4 cm
In ∆DEL, ∠DLE = 90°
52 = EL2 + 42 (putting the values)
25 = EL2 + 16
25 – 16 = EL2
⇒ EL2 = 9
EL = √9
∴ EL = 3 cm
⇒ Area of ∆DEF = 4×3
∴ Area of ∆DEF = 12 cm2→ eqn4
R = 4 cm
⇒ Area of semicircle = 3.14×8
∴ Area of semicircle = 25.12 cm2→ eqn5
Area of whole figure = eqn1 + eqn2 + eqn3 + eqn4 + eqn5
⇒ Area of whole figure = 32 + 32 + 64 + 12 + 25.12
∴ Area of whole figure = 165.12 cm2
Area of the whole figure is 165.12 cm2.
Q.54. A circular disc of radius 6 cm is divided into three sectors with central angles 90°, 120° and 150°. What part of the whole circle is the sector with central angle150°? Also, calculate the ratio of the areas of the three sectors.
θ1 = 90° θ2 = 120°, θ3 = 150°
Radius of circle = r = 6 cm
Area of circle = πR2
⇒ Area of circle = π×62
⇒ Area of circle = 36π → eqn2
Area of sector (θ2) = 12π cm2→ eqn3
Area of sector (θ1) = 9π cm2→ eqn4
Ratio of three sectors ∷ 9π:12π:15π
Ratio of three sectors ∷ 3:4:53:4:5
Q.55. A round table cover has six equal designs as shown in the given figure. If the radius of the cover is 35 cm then find the total area of the design. [Use √3 = 1.732 and π = 3.14.]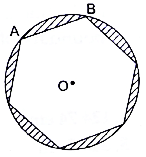
Total area of design = Area of all the minor segments
Here we will find out the area of one segment and then multiply it with 6 to get the total area of design. And as the figure inscribed in the circle is a regular hexagon this implies that it will be having all edges of same length. Therefore we can say that the angle subtended by each chord which are actually the edges of regular hexagon are equal(theorem).
Let angle subtended by chord AB on centre O be θ
∴ Angle subtended = θ = 60°
Radius of circle = 35 cm
Area of minor segment OAB = Area of sector – Area of ∆OAB
Area of minor segment OAB = 641.0833333 – 530.425
∴ Area of minor segment OAB = 110.6583333 cm2→ eqn2
Total area of design = 6 × Area of minor segment OAB
⇒ Total area of design = 6×110.6583333 (from eqn2)
∴ Total area of design = 663.95 cm2
Total area of design is 663.95 cm2.
Q.56. In the given figure, PQ = 24 cm, PR = 7 cm and 0 is the centre of the circle. Find the area of the shaded region. [Take π = 3.14.]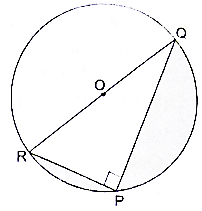
Here we will subtract the area of right angle triangle PQR and semicircle from the area of entire circle.
Given PQ = 24 cm, PR = 7 cm
Consider ∆PQR, ∠QPR = 90°
RQ2 = 242 + 72
⇒ RQ2 = 576 + 49
⇒ RQ2 = 625
Therefore Radius of the circle = half of RQ
Let radius be ‘r’
r = 25/2
∴ r = 12.5 cm
Area of ∆PQR = 7×12
∴ Area of ∆PQR = 84 cm2→ eqn1
∴ Area of semicircle = 245.3125 cm2→ eqn2
Area of circle = πr2
Area of circle = π(12.52)
⇒ Area of circle = 3.14×156.25 (putting π = 3.14)
∴ Area of circle = 490.625 cm2→ eqn3
Area of shaded region = eqn3 – eqn2 – eqn1
⇒ Area of shaded region = 490.625 – 245.3125 – 84
∴ Area of shaded region = 161.3125 cm2
Area of shaded region is 161.3125 cm2.
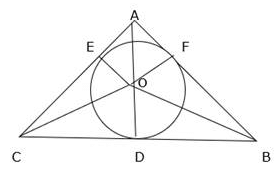
Q.57. In the given figure, ΔABC is right-angled at A. Find the area of the shaded region if AB = 6 cm, BC = 10 cm and 0 is the centre of the incircle of ΔABC. [Take π = 3.14.]
Given AB = 6 cm, BC = 10 cm
Consider ∆ABC, ∠BAC = 90°
⇒ 102 = 62 + AC2 (putting given values)
⇒ 100 = 36 + AC2
⇒ 100 – 36 = AC2
⇒ AC2 = 64
AC = √64
∴ AC = 8 cm
Join OB, OA, OC, OE, OF, OD
Here OE = OF = OD = radius of circle = r cm
∠OEC = ∠ODB = ∠OFB = 90° (angle at the point of contact of radius & tangent)
Area ∆ABC = Area of ∆OAC + Area of ∆OCB + Area of ∆OAB → eqn1
∴ Area of ∆OAC = 4r → eqn2
∴ Area of ∆OCB = 5r → eqn3
∴ Area of ∆OAB = 3r → eqn4
⇒ Area of ∆ABC = 3×8
∴ Area of ∆ABC = 24 cm2→ eqn5
Putting all the values in equation we get;
⇒ 24 = 4r + 5r + 3r
⇒ 24 = 12r
r = 24/12
∴ r = 2 cm
Area of circle = πr2
Put the value of r, we get,
⇒ Area of circle = π×22
⇒ Area of circle = 3.14×4 (putting π = 3.14)
∴ Area of circle = 12.56 cm2→ eqn6
Area of shaded region = Area of triangle – Area of circle
⇒ Area of shaded region = 24 – 12.56 (from eqn5 and eqn6)
∴ Area of shaded region = 11.44 cm2
Area of shaded region is 11.44 cm2.
Q.58. In the given figure, ΔABC is right-angled at A. Semicircles are drawn on AB, AC and BC as diameters. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.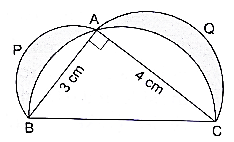
Here we will first find out the area of semicircle whose diameter is BC and then subtract the area of right angle triangle ABC from it and then we will subtract this result from the area of semicircles whose diameters are AB and AC.
Consider ∆ABC, ∠BAC = 90°
⇒ BC2 = 42 + 32
⇒ BC2 = 16 + 9
⇒ BC2 = 25
BC = √25
∴ BC = 5 cm
Area of semicircle whose diameter is AC
∴ Radius = 2 cm
∴ Area of semicircle = 2π cm2 –eqn2
Area of semicircle whose diameter is AB
Radius = AB/2
Radius = 3/2
∴ Radius = 1.5 cm
∴ Area of semicircle = 1.125π cm2→ eqn3
Area of semicircle whose diameter is BC
Radius = BC/2
Radius = 5/2
∴ Radius = 2.5 cm
∴ Area of semicircle = 3.125π cm2→ eqn4
⇒ Area of triangle PQR = 3×2
∴ Area of triangle PQR = 6 cm2→ eqn5
Now subtract equation 5 from equation 4,
⇒ Area of semicircle excluding ∆ABC = eqn4 – eqn5
⇒ Area of semicircle excluding ∆ABC = 3.125π – 6
∴ Area of semicircle excluding ∆ABC = 3.8214 cm2→ eqn6
Area of shaded region = eqn3 + eqn2 – eqn6
⇒ Area of shaded region = 2π + 1.125π – 3.8214
⇒ Area of shaded region = 3.125π – 3.8214
⇒ Area of shaded region = 9.8214 – 3.8214
∴ Area of shaded region = 6 cm2
Area of shaded region 6 cm2.
Q.59. PQRS is a diameter of a circle of radius 6 cm. The lengths PQ, QR and RS are equal. Semicircles are drawn with PQ and QS as diameters, as shown in the given figure. If PS = 12 cm, find the perimeter and area of the shaded region. [Take π = 3.14.]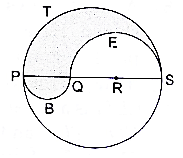
Here we will subtract the area of semicircle whose diameter is QS from the area of the semicircle whose diameter PS and add the area of semicircle whose diameter is PQ so as to find out the area of the shaded region.
Given PS = 12 cm
Radius of the circle = 6 cm
PQ = QR = RS
So let PQ = QR = RS = k cm
Also, PQ + QR + RS = PS
⇒ k + k + k = 12
⇒ 3k = 12
k = 12/3
∴ k = 4 cm
So, PQ = QR = RS = 4 cm
Area and perimeter of semicircle whose diameter is PS
Radius = PS/2
Radius = 12/2
∴ Radius = 6 cm
∴ Area of semicircle = 18π cm2→ eqn2
Perimeter of semicircle = πr
⇒ Perimeter of semicircle = π×6
∴ Perimeter of semicircle = 6π cm → eqn3
Area of semicircle whose diameter is QS
Radius = QS/2
Radius = 8/2
⇒ Radius = 4 cm
∴ Area of semicircle = 8π cm2→ eqn4
Perimeter of semicircle = πr
⇒ Perimeter of semicircle = π×4
∴ Perimeter of semicircle = 4π cm → eqn5
Area of semicircle whose diameter is PQ
Radius = PQ/2
Radius = 4/2
∴ Radius = 2 cm
∴ Area of semicircle = 2π cm2→ eqn6
Perimeter of semicircle = πr
⇒ Perimeter of semicircle = π×2
∴ Perimeter of semicircle = 2π cm → eqn7
Area of the shaded region = eqn2 – eqn4 + eqn6
Area of shaded region = 18π – 8π + 2π
⇒ Area of shaded region = 12π
⇒ Area of shaded region = 12×3.14 (putting π = 3.14)
∴ Area of shaded region = 37.68 cm2
Perimeter of shaded region = eqn3 – eqn5 + eqn7
⇒ Perimeter of shaded region = 6π -4π + 2π
⇒ Perimeter of shaded region = 4π
⇒ Perimeter of shaded region = 4×3.14 (put π = 3.14)
∴ Perimeter of shaded region = 12.56 cm
Perimeter of the shaded region is 12.56 cm and Area of shaded region is 37.68 cm2.
Q.60. The inside perimeter of a running track shown in the figure is 400 m. The length of each of the straight portions is 90 m, and the ends are semicircles. If the track is 14 m wide everywhere, find the area of the track. Also, find the length of the outer boundary of the track.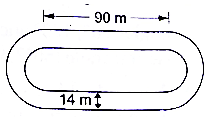
Consider the figure as a combination of two semicircles on the ends of the rectangle
Let the length of rectangle be ‘L’ m and breadth be ‘B’ cm
Given L = 90 m, W = 14 m
Perimeter of running track = 400 m
Perimeter of inside of running track = 2L + Arc of two semicircles → eqn1
Arc length of a semicircle = πr where r = radius
⇒ 400 = (2×90) + (2×πr) (putting values in eqn1)
⇒ 400 = 180 + 2πr
⇒ 400 – 180 = 2πr
⇒ 220 = 2πr
∴ r = 35 m
Area of inner of running track = Area of rectangle + 2×area of semicircles → eqn2
Area of rectangle = L×B
Here B = 2r
B = 70 m
⇒ Area of inner rectangle = 90×70
∴ Area of inner rectangle = 6300 m2→ eqn3
⇒ Area of inner semicircles = 1225π
⇒ Area of inner semicircle = 175×22
∴ Area of inner semicircle = 3850 m2→ eqn4
Area of inner of running track = 6300 + 3850 (from3&4)
∴ Area of inner of running track = 10150 m2
Now radius of semicircles of outer of the running track = R = r + W
⇒ R = 35 + 14
∴ R = 49 m
⇒ Area of outer semicircles = 2401π
⇒ Area of outer semicircles = 343×22
∴ Area of outer semicircle = 7546 m2→ eqn5
Breadth of outer running track = B’ = 2R
⇒ B’ = 2×49
∴ B’ = 98 m
Area of outer rectangle = L×B’
⇒ Area of outer rectangle = 90×98
∴ Area of outer rectangle = 8820 m2→ eqn6
Area of entire ground = 8820 + 7546 (from 5&6)
∴ Area of entire ground = 16366 m2
Area of running track = Area of entire ground – Area of inner ground
⇒ Area of running track = 16366 – 10150
∴ Area of running track = 6216 m2
Perimeter of outer boundary = 2L + Arc of outer semicircles
Arc length of an outer semicircle = πR, where R = outer radius
⇒ Perimeter of outer boundary = 180 + (2×22×7)
⇒ Perimeter of outer boundary = 180 + 308
∴ Perimeter of outer boundary = 488 m
Area of running track is 6216 m2 and perimeter of outer boundary is 488 m.
|
53 docs|15 tests
|
|
53 docs|15 tests
|

|
Explore Courses for Class 10 exam
|

|
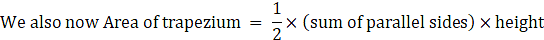

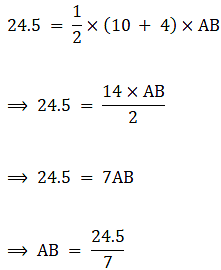
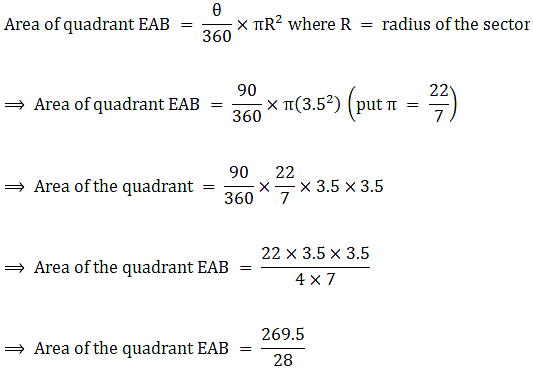
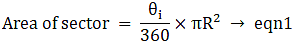
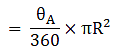
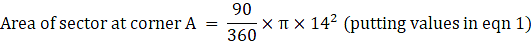

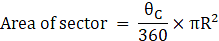
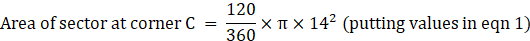

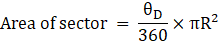
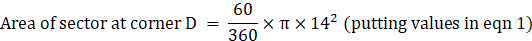
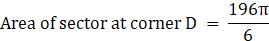
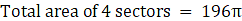
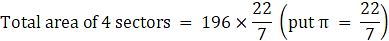
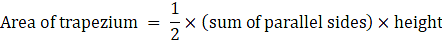
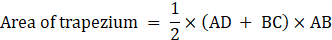
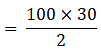
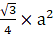
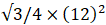 (putting the value of a)
(putting the value of a)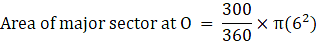
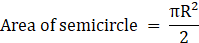
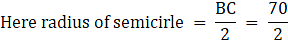

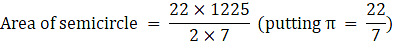

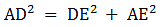
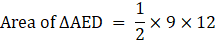




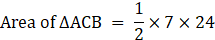
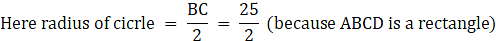

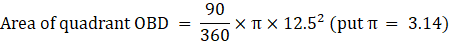

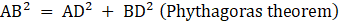
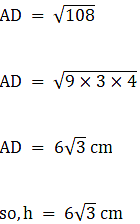


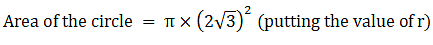

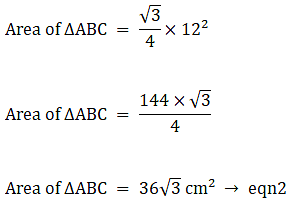
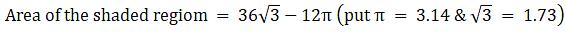
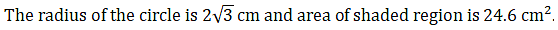




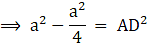
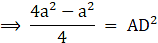
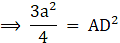
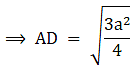
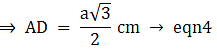
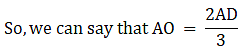
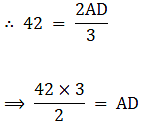
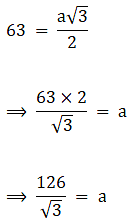
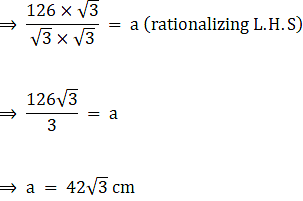
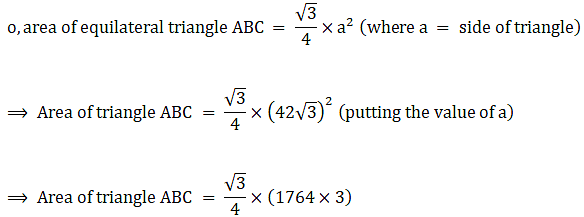
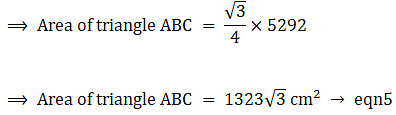
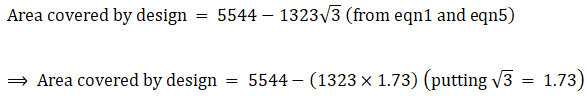

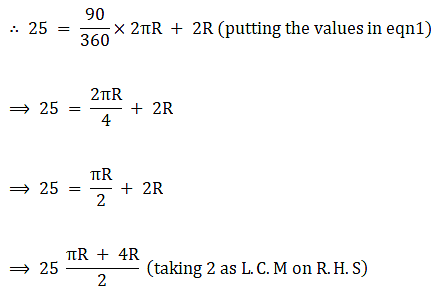
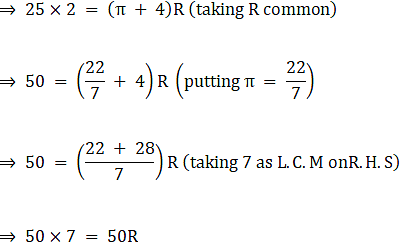
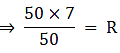
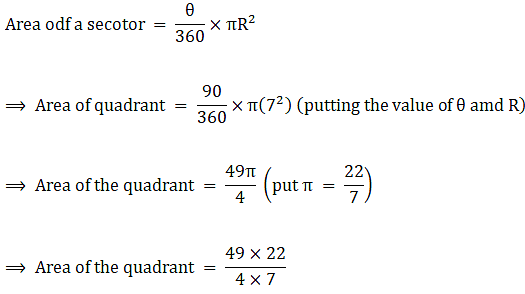
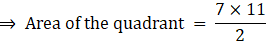
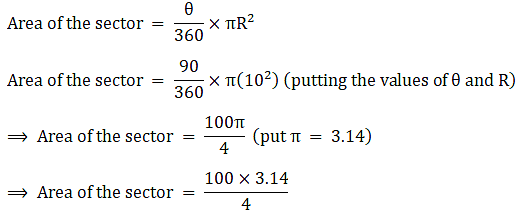
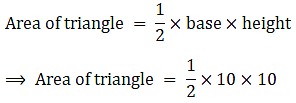
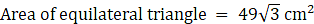


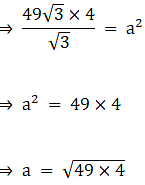

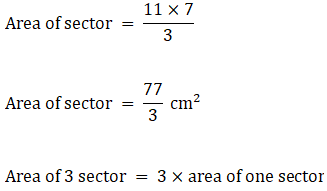
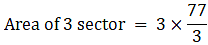
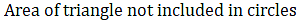
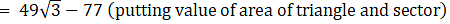

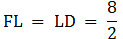
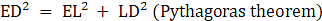
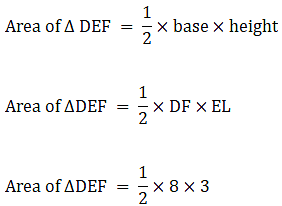

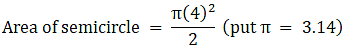

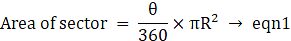
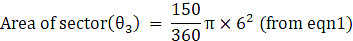
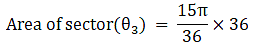
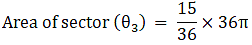
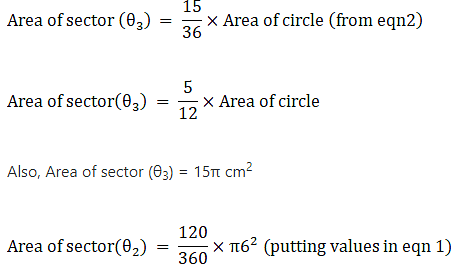
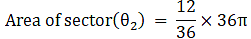
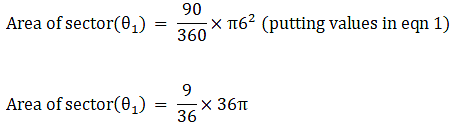
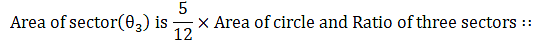 3:4:5
3:4:5