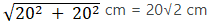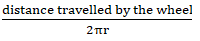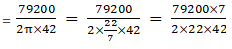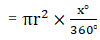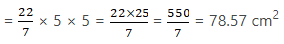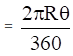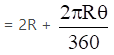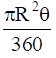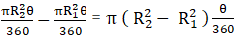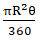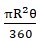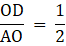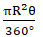RS Aggarwal Solutions: Area of Circle, Sector and Segment- 5 - Class 10 PDF Download
Formative Assessment (Unit Test)
Q.1. In the given figure, a square OABC has been inscribed in the quadrant OPBQ. If OA = 20 cm then the area of the shaded region is [take π = 3.14]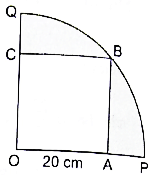
(a) 214 cm2
(b) 228 cm2
(c) 242 cm2
(d) 248 cm2
Length of side of square = OA = 20 cm
Radius of Quadrant = OB =
Area of Quadrant = πR2 × θ/360 = 3.14 × 20√2 × 20√2 × 90/360 = 628 cm2
Area of Square = a2 = 202 cm2 = 400 cm2
Area of Shaded region = Area of Quadrant - Area of Square
= 628 cm2 – 400 cm2
= 228 cm2
Q.2. The diameter of a wheel is 84 cm. How many revolutions will it make to cover 792 m?
(a) 200
(b) 250
(c) 300
(d) 350
Diameter of wheel = 84 cm
Radius of wheel = r = 84/2 cm = 42 cm
Distance the wheel travels = 792 m = 79200 cm
In 1 revolution wheel travels 2πr distance
No. of revolutions a wheel makes =
= 300 revolutions
Q.3. The area of a sector of a circle with radius r, making an angle of x° at the centre is x
(a) 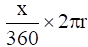
(b) 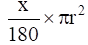
(c) 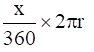
(d) 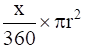
Area of a sector of angle θº of a circle with radius R = area of circle × θ/360
Q.4. In the given figure, ABCD is a rectangle inscribed in a circle having length 8 cm and breadth 6 cm. If π = 3.14 then the area of the shaded region is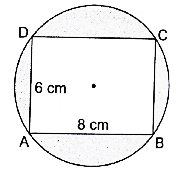
(a) 264 cm2
(b) 266 cm2
(c) 272 cm2
(d) 254 cm2
Given:
Length of rectangle = 8 cm
Breadth of rectangle = 6 cm
Area of rectangle = length × breadth
= 8 × 6 = 48 cm2
Consider ΔABC,
By Pythagoras theorem,
AC2 = AB2 + BC2
= 82 + 62 = 64 + 36 = 100
AC = √100 = 10 cm
⇒ Diameter of circle = 10 cm
Thus, radius of circle = 10/2 = 5cm
Let the radius of circle be r = 5 cm
Then, Area of circle = πr2
Area of shaded region = Area of circle – Area of rectangle
= 78.57 - 48
= 30.57 cm2
Hence, the area of shaded region is 30.57 cm2.
Q.5. The circumference of a circle is 22 cm. Find its area. [Take π = 22/7]
Let the radius if circle be r
Circumference of circle = 22 cm
2πr = 22 cm
2 × 22/7 × r = 22 cm
r = 22 × 1/2 ×7/22 cm
r = 3.5 cm
Area of Circle = πr2
= 22/7 × 3.5 × 3.5 cm2
= 38.5 cm2
∴ Area of Circle = 38.5 cm2
Q.6. In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the length of the arc.
Radius of circle = R = 21 cm
Angle subtended by arc = 60°
Length of an arc of a sector of angle θº of a circle with radius R
= Circumference of circle × θ/360
Length of arc = 2 × 22/7 × 21 × θ/360 cm = 22 cm
Length of arc = 22 cm
Q.7. The minute hand of a clock is 12 cm long. Find the area swept by it in 35 minutes.
Length of the minute hand of a clock = 12 cm
∴ Radius = R = 12 cm
In 1 minute, minute hand sweeps 6°
So, in 35 minutes, minute hand will sweep 35 × 6° = 210°
Area swept by minute hand in 35 minutes = Area of a sector of angle θº of a circle with radius R == 22/7 × 12 × 12 × 60°/360° = 264 cm2
Area swept by minute hand in 35 minutes = 264 cm2
Q.8. The perimeter of a sector of a circle of radius 5.6 cm is 27.2 cm. Find the area of the sector.
Radius of circle = 5.6 cm
Perimeter of a sector of a circle = 2R + Circumference of circle × θ/360
Perimeter of a sector of a circle = 2 × 5.6 + 2 × 22/7 × 5.6 × θ/360 cm
= 27.2 cm
⇒ 2 × 22/7 × 5.6 × θ/360 = 27.2 – 11.2 cm = 16 cm
⇒ θ = 16 × 1/2 × 1/5.6 × 7/22
⇒ θ = 163.63°
Area of Sector = πr2 × θ\360 = 22/7 × 5.6 × 5.6 × 163.63/360 = 44.8cm2
∴ Area of Sector = 44.8 cm2
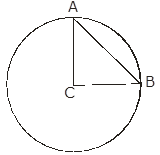
Q.9. A chord of a circle of radius 14 cm makes a right angle at the centre. Find the area of the sector.
Chord AB subtends an angle of 90° at the centre of the circle
Radius of Circle = R = 14 cm
Area of sector of circle of radius R =
= 22/7 × 14 × 14 × 90/360 cm2 = 154 cm2
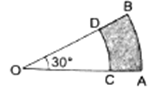
Q.10. In the give figure, the sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area of the shaded region.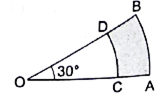
Given,
Radius of smaller circle = R1 = 3.5 cm
Radius of bigger circle = R2 = 7 cm
Angle subtended = 30°
Area of Shaded region =
= 22/7 × (72 – 3.52) × 30/360 cm2
= 22/7 × (49 – 12.22) × θ/360 cm2
= 9.625 cm2
∴ Area of shaded region = 9.625 cm2
Q.11. A wire when bent in the form of an equilateral triangle encloses an area of 121√3 cm2. If the same wire is bent into the form of a circle, what will be the area of the circle? [Take π = 22/7]
Let the sides of equilateral triangle be a cm
Area of equilateral triangle = 121√3 cm2
Area of equilateral triangle = √3/4 × a2
⇒ √3/4 a2 = 121√3
⇒ a2 = 121√3 × 4/√3 = 121 × 4 cm2
⇒ a2 = 484 cm2
⇒ a = 22 cm
Perimeter of equilateral triangle = 3a
= 3 × 22 cm = 66 cm
Perimeter of equilateral triangle = Circumference of circle
Circumference of circle = 66 cm
Let the radius of circle be r
Circumference of circle = 2πr
⇒ 2πr = 66 cm
⇒ 2 × 22/7 × r = 66 cm
⇒ r = 66 × 1/2 × 7/22 cm
⇒ r = 10.5 cm
Area of circle = πr2 = 22/7 × 22/7 × 10.5 × 10.5 cm2
= 346.5 cm2
Q.12. The wheel of a cart is making 5 revolutions per second. If the diameter of the wheel is 84 cm, find its speed in km per hour. [Take π = 22/7]
Diameter of the wheel = 84 cm
Let the radius of the wheel be R cm
Radius of the wheel = 84/2 cm = 42 cm
No. of revolutions wheel makes = 5 rev/sec
Since, 1 revolution = 2πR
Speed of the wheel = 5 × 2πR rev/sec
= 5 × 2 × 22/7 × 42 = 1320 cm/sec
= 13.20 m/sec
= 13.20 × 3600/1000 km/h
= 47.52 km/h
Since, 1 m/sec = 3600/1000 km/h
Q.13. OACB is a quadrant of a circle with centre O and its radius is 3.5 cm. If OD = 2 cm, find the area of (i) the quadrant OACB (ii) the shaded region. [Take π = 22/7]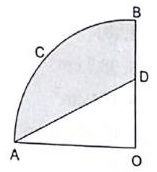
Radius of circle = R = 3.5 cm
OD = 2 cm
OA = OB = R = 3.5 cm
Since, OACB is a quadrant of a circle ∴ angle subtended by it at the centre = 90°
(i) Area of quadrant =
= 22/7 × 3.5 × 3.5 × 90°/360° cm2
= 9.625 cm2
(ii) Area of shaded region = Area of quadrant – Area of triangle OAD
Area of triangle OAD = 1/2 × base × height
= 1/2 × OA × OD
= 1/2 × 3.5 × 2 cm2
= 3.5 cm2
Area of shaded region = 9.625 cm2 – 3.5cm2
= 6.125 cm2
Q.14. In the given figure, ABCD is a square each of whose sides measures 28 cm. Find the area of the shaded region. [Take π = 22/7]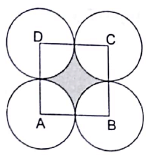
Length of the sides of square = 28 cm
Area of square = a2 = 282 cm2
= 784 cm2
Since, all the circles are identical so, they have same radius
Let the radius of circle be R cm
From the figure 2R = 28 cm
R = 28/2 cm
R = 14 cm
Quadrant of a circle subtends 90° at the centre.
Area of quadrant of circle =
= 22/7 × 14 × 14 × 90°/360° cm2 = 154 cm2
Area of 4 quadrants of circle = 154 × 4 cm2 = 616 cm2
Area of shaded region = Area of square – Area of 4 quadrants of circle
= 784 cm2 – 616 cm2
= 168 cm2
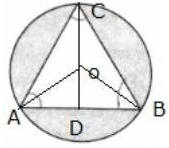
Q.15. In the given figure, an equilateral triangle has been inscribed in a circle of radius 4 cm. Find the area of the shaded region. [Take π = 3.14 and √3 = 1.73]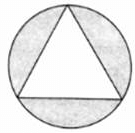
Radius of circle = R = 4 cm
OD perpendicular to AB is drawn
ΔABC is equilateral triangle,
∠A = ∠B = ∠C = 60°
∠OAD = 30°
OD/AO = sin 30°
AO = 4 cm
OD = 1/2 × 4 cm
OD = 2 cm
AD2 = OA2 – OD2
= 42 – 22 = 16 – 4 = 12 cm2
AD = 2√3 cm
AB = 2 × AD
= 2 × 2√3 cm = 4√3 cm
Area of triangle ABC = √3/4 × AB2
= √3/4 × 4√3 × 4√3
= 20.71 cm2
Area of circle = πR2
= 3.14 × 4 × 4 cm2
= 50.24 cm2
Area of shaded region = 29.53 cm2
Q.16. The minute hand of a clock is 7.5 cm long. Find the area of the face of the clock described by the minute hand in 56 minutes.
Length of minute hand = 7.5 cm
In a clock, length of minute hand = radius
Radius = R = 7.5 cm
In 1 minute, minute hand moves 6°
So, in 56 minutes, minute hand moves 56 × 6° = 336°
Area described by minute hand =
= 22/7 × 7.5 × 7.5 × 336°/360° cm2
= 165 cm2
Q.17. A racetrack is in the form of a ring whose inner circumference is 352 m and outer circumference is 396 m. Find the width and the area of the track.
Let the inner radius be R1 and outer radius be R2
Inner circumference = 2πR1 = 352 m
⇒ 2 × 22/7 × R1 = 352 m
⇒ R1 = 352 × 1/2 × 7/22
⇒ R1 = 56 m
Outer Circumference = 2πR2 = 396 m
⇒ 2 × 22/7 × R2 = 396 m
⇒ R2 = 396 × 1/2 × 7/22 m
⇒ R2 = 63 m
Width of the track = R2 – R1 = 63 m – 56 m = 7 m
Area of track == 22/7 × (632 -562)
= 22/7 × (3969 – 3136) m2
= 22/7 × 833 m2 = 2618 m2
Q.18. A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the areas of the minor and major segments. [Take π = 22/7 and √3 = 1.732.]
∠ACB = 60°
Chord AB subtends an angle of 60° at the centre
Radius = 30 cm
Let Radius be R
In triangle ABC, AC = BC
So, ∠CAB = ∠CBA
∠ ACB + ∠ CAB + ∠ CBA = 180°
60° + 2∠CAB = 180°
2∠CAB = 180° - 60° = 120°
∠CAB = 120°/2 = 60°
∠CAB = ∠CBA = 60°
∴ ΔABC is a equilateral triangle
Length of side of an equilateral triangle = radius of circle = 30 cm
Area of equilateral triangle = √3/4 × side2 = 1.732/4 × 30 × 30 cm2
= 389.7 cm2
Area of sector ACB == 3.14 × 30 × 30 × 60°/360° = 471.45 cm2
Area of minor Segment = Area of sector ACB – Area of ΔABC
= 471.45 cm2 – 389.7 cm2 = 81.75 cm2
Area of circle = πR2 = 3.14 × 30 × 30 cm2 = 2828.57 cm2
Area of major segment = Area of circle – Area of minor segment
= 2826 cm2 – 81.75 cm2
= 2744.25 cm2
Q.19. Four cows are tethered at the four corners of a square field of side 50 m such that each can graze the maximum unshared area. What area will be left ungrazed? [Take π = 3.14]
From the figure we see that cows are tethered at the corners of the square so while grazing they form four quadrants as shown in the figure
Length of side of square = 50 m
Length of side of square = 2 × Radius of quadrant
Radius of quadrant = R = 50/2 m
= 25 m
Area of square = side2
= 502 m2 = 2500 m2
Area of quadrant = 1/4 π R2 = 1/4 × 3.14 × 25 × 25 m2
= 490.625 m2
Area of 4 quadrants = 4 × 490.625 m2
= 1962.5 m2
Area left ungrazed = Area of shaded part
= Area of square – Area of 4 quadrants
= 2500 m2 – 1962.5 m2
= 537.5 m2
Q.20. A square tank has an area of 1600 m2. There are four semicircular plots around it. Find the cost of turfing the plots at Rs. 12.50 per m2. [Take π = 3.14]
Let the length of side of the square tank be a
Area of square tank = a2 = 1600 m2
⇒ a = √1600 m = 40 m
Let the radius of semicircle be R
From the figure we can see that
Length of the side of the square = Diameter of semicircle
40 m = 2 × R
R = 40/2 m
R = 20 m
Area of semi-circle = 1/2 πR2 = 1/2 × 3.14 × 20 × 20 m2
= 628 m2
Area of 4 semi-circles = 4 × 628 m2
= 2512 m2
Cost of turfing the plots = Rs. 12.50 per m2
Cost of Turfing = Cost of turfing per m2 × Area of 4 semicircle
= Rs. 12.50 × 2512
= Rs. 31400