Methods of Finding Square Roots | The Complete SAT Course - Class 10 PDF Download
| Table of contents |

|
| Introduction to Square Root |

|
| Finding Square Root using Different Methods |

|
| Square Root Table |

|
| Square Root Formula |

|
| Square of a Number |

|
| Squares and Square Roots |

|
Introduction to Square Root
The concept of square root is the inverse of squaring a number. It is the value that is obtained when we multiply a number by itself. The square of any number is always a positive number, which means every number has two square roots. In this article, we will explore the definition of square root, its representation, and how to find it using various methods.
Definition and Representation of Square Root
The square root of a number is the value of power 1/2 of that number. It is represented using the symbol '√ ', where the number under the square root symbol is called the radicand. The square root symbol is called a radical.
Finding Square Root using Different Methods
There are four methods to find the square root of a number - Repeated Subtraction Method, Prime Factorization Method, Estimation Method, and Long Division Method. The first three methods work only for perfect square numbers, while the fourth method can be used for any number, whether it is a perfect square or not.
- Repeated Subtraction Method: This method involves subtracting consecutive odd numbers from the number for which we are finding the square root, till we reach 0. The number of times we subtract is the square root of the given number. This method works only for perfect square numbers.
- Prime Factorization Method: In this method, we first divide the given number into its prime factors. Then, we form pairs of factors such that both factors in each pair are equal. Next, we take one factor from each pair and find their product, which is the square root of the given number.
- Estimation Method: This method involves approximating the square root of a number by finding the closest perfect square below the number and then taking the difference between the given number and the perfect square. We then divide this difference by twice the perfect square and add it to the square root of the perfect square to get an estimate of the square root of the given number.
- Long Division Method: This method involves long division to find the square root of a number. It can be used for any number, whether it is a perfect square or not. The method involves grouping the digits of the number into pairs from the right-hand side and finding the largest number whose square is less than or equal to the first pair of digits. We then subtract the square of this number from the first pair and bring down the next pair of digits. We repeat this process until we have found the square root of the given number.
Repeated Subtraction Method of Square Root
The repeated subtraction method of finding square roots involves subtracting consecutive odd numbers from the given number until we reach 0. The number of times we subtract is the square root of the given number. This method only works for perfect square numbers.
Example:
To find the square root of 16 using the repeated subtraction method, we subtract consecutive odd numbers from 16 until we reach 0:
16 - 1 = 15
15 - 3 = 12
12 - 5 = 7
7 - 7 = 0
We have subtracted 4 times, so the square root of 16 is 4.
Prime Factorization Method
Prime factorization of any number means to represent that number as a product of prime numbers. To find the square root of a given number through the prime factorization method, we follow the steps given below:
Step 1: Divide the given number into its prime factors.
Step 2: Form pairs of factors such that both factors in each pair are equal.
Step 3: Take one factor from each pair.
Step 4: Find the product of the factors obtained by taking one factor from each pair.
Step 5: That product is the square root of the given number.
Example:
Let's find the square root of 144 using the prime factorization method.
Step 1: Prime factorization of 144 is 2 x 2 x 2 x 2 x 3 x 3.
Step 2: Form pairs of factors as (2 x 2), (2 x 2), and (3 x 3).
Step 3: Take one factor from each pair, which gives 2 x 2 x 3 = 12.
Step 4: The product obtained is the square root of 144.
Step 5: Therefore, √144 = 12.
This method can be used to find the square root of any number, not necessarily just perfect squares. However, for numbers with large prime factors, this method can become quite complicated and time-consuming.
Finding Square Root by Estimation Method
- The estimation method is a useful approach to approximate the square root of a given number. To apply this method, we first identify the nearest perfect square numbers to the given number. For example, if we want to find the square root of 15, the nearest perfect squares are 9 and 16. Using the square roots of these perfect squares, we can determine that the square root of 15 is between 3 and 4.
- To refine our estimate, we can consider the mid-point between 3 and 4, which is 3.5. We can then square 3.5 and 4 to determine which one is closer to 15. It turns out that 4 is closer, so we know that the square root of 15 is between 3.5 and 4.
- To further refine our estimate, we can consider the mid-point between 3.8 and 3.9, since these values are closer to our current estimate range. By squaring these values, we can determine that the square root of 15 is between 3.8 and 3.9. We can continue this process of narrowing our estimate range until we reach a desired level of accuracy. In this case, we found that the square root of 15 is approximately 3.872. However, it should be noted that this method can be time-consuming for large or complex numbers.
Calculating Square Root by Long Division Method
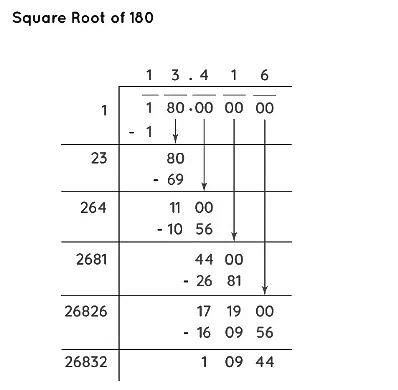
Long division is a method for dividing large numbers into steps or parts, breaking the division problem into a sequence of easier steps. We can find the exact square root of any given number using this method. Let us understand the process of finding square root by the long division method with an example. Let us find the square root of 180.
- Step 1: Place a bar over every pair of digits of the number starting from the units' place (right-most side). We will have two pairs, i.e., 1 and 8
- Step 2: We divide the left-most number by the largest number whose square is less than or equal to the number in the left-most pair.
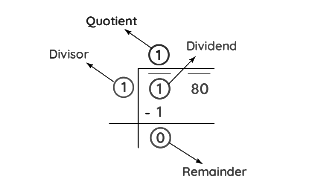
- Step 3: Bring down the number under the next bar to the right of the remainder. Add the last digit of the quotient to the divisor. To the right of the obtained sum, find a suitable number which, together with the result of the sum, forms a new divisor for the new dividend that is carried down.
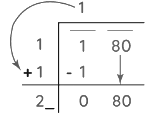
- Step 4: The new number in the quotient will have the same number as selected in the divisor. The condition is the same — as being either less than or equal to the dividend.
- Step 5: Now, we will continue this process further using a decimal point and adding zeros in pairs to the remainder.
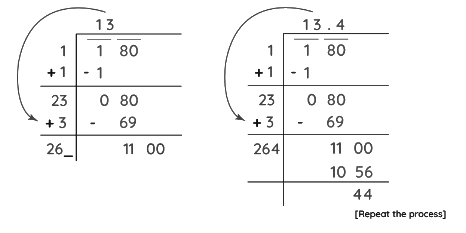
- Step 6: The quotient thus obtained will be the square root of the number. Here, the square root of 180 is approximately equal to 13.4 and more digits after the decimal point can be obtained by repeating the same process as follows.
Square Root Table
The square root table consists of numbers and their square roots. It is useful to find the squares of numbers as well. Here is the list of square roots of perfect square numbers and some non-perfect square numbers from 1 to 10.
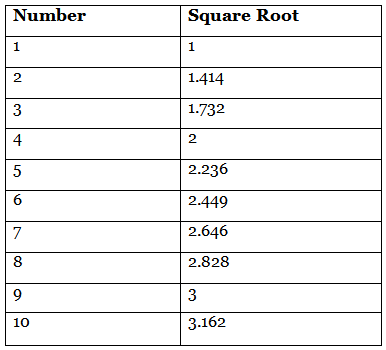
Note that: The square roots of perfect squares (like 1, 4, 9, etc.) are rational numbers, while the square roots of non-perfect squares (like 2, 3, 5, etc.) are irrational numbers that go on forever without repeating.
Square Root Formula
The formula for calculating the square root of a number is √x = x(1/2), where x is the number whose square root we want to find. The exponent formula for any number is: n√x = x(1/n), where n is the root we want to find. For example, when we want to find the cube root of a number, n = 3. However, when we specifically want to find the square root of a number, n = 2. We can use various methods to calculate the square root of a number, including prime factorization, estimation, long division method, and so on. The general form of writing the square root of a number is √x = x(1/2).
Square Root of a Negative Number
- When we try to find the square root of a negative number, it is not possible to obtain a real number as the result, because the square of any real number is either positive or zero. However, complex numbers can provide solutions for the square root of a negative number. The principal square root of -x is represented as √(-x) = i√x, where 'i' is the square root of -1.
- For instance, consider the perfect square number 16. If we try to calculate the square root of -16, we won't obtain a real square root. Instead, we can use the formula √(-16) = √16 × √(-1) = 4i, where 'i' is equivalent to the square root of -1. Therefore, 4i is one of the square roots of -16.
Square of a Number
The square of a number is obtained by raising the number to the power of two, denoted as y2, which is known as the square of the base. For instance, 5 raised to the power of two, denoted as 52 or 25, is called the square of 5, and 8 raised to the power of two, denoted as 82 or 64, is called the square of 8. To find the square of a number, we simply multiply the number by itself or perform the operation of squaring. For example, the square of 5, denoted as 52, is equal to 5 × 5 = 25, and the square of 8, denoted as 82, is equal to 8 × 8 = 64. When we square a whole number, the result is always a perfect square, such as 4, 9, 16, 25, 36, 49, 64, and so on. It is important to note that the square of any number is always a positive number.
How to Find the Square of a Number?
The square of a number can be found by multiplying a number by itself. For single-digit numbers, we can use multiplication tables to find the square, while in the case of two or more than two-digit numbers, we perform multiplication of the number by itself to get the answer. For example, 9 × 9 = 81, where 81 is the square of 9. Similarly, 3 × 3 = 9, where 9 is the square of 3.
Here are a few more examples:
72 = 7 × 7 = 49
11² = 11 × 11 = 121
(-3)² = (-3) × (-3) = 9
(2.5)² = 2.5 × 2.5 = 6.25
It's important to note that the square of a number is always positive, even if the original number is negative. Also, the square of a fraction or decimal can be found by multiplying the numerator and denominator (or decimal value) separately and then simplifying the result if possible.
Squares and Square Roots
There is very strong relation between squares and square roots as each one of them is the inverse relation of the other. i.e., if x2 = y then x = √y. It can be simply remembered like this:
- When "square" is removed from one side of the equation, we get the square root on the other side.
For example, 42 = 16 means, 4 = √16. This is also known as "taking square root on both sides". - When "square root" is removed from one side of the equation, we get square on the other side.
For example, √25 = 5 means, 25 = 52. This is also known as "squaring on both sides"
This logic helps in solving many equations in algebra. Consider the following example:
Example: Solve the equation √(2x + 3) = 10.
Squaring on both sides of the equation would result in the cancellation of the square root on the left side.
2x + 3 = 102
2x + 3 = 100
2x = 97
x = 97/2 = 48.5
|
405 videos|217 docs|164 tests
|















