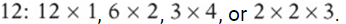Introduction to Factoring | The Complete SAT Course - Class 10 PDF Download

Factoring

There are many ways to factor
Therefore, 1, 2, 3, 4, 6, and 12 are the factors of 12.

Example:

Two bells, A and B, ring simultaneously, then bell A rings every 168 seconds and bell B rings every 360 seconds. What is the minimum number of seconds between simultaneous rings?
This question is asking for the least common multiple of 168 and 360. The prime factorization of 168 is 2 x 2 x 2 x 3 x 7 and the prime factorization of 360 is 2 x 2 x 2 x 3 x 3 x 5. A common multiple must have all of the factors that each of these numbers has, and the smallest of these is 2 x 2 x 2 x 3 x 3 x 5 x 7. So they ring together every 2,520 seconds.

The Law of FOIL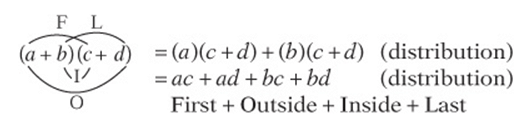

Factoring Formulas

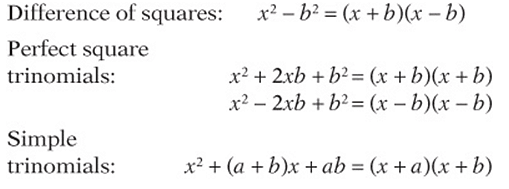
Example:

Factor x² - 36.
This is a “difference of squares”: x² - 36 = (x - 6)(x + 6).
Factor x² - 5x - 14
This is a simple trinomial. Look for two numbers that have a sum of –5 and a product of –14. With a little guessing and checking, you will see that –7 and 2 work. So x² - 5x - 14 = (x - 7)(x + 2).

The Zero Product Property

Solve x² - 5x - 14 = 0 .
Factor: (x - 7)(x + 2)
Since their product is 0, either  x - 7 = 0 or x + 2 = 0 , so  x = 7 or –2.

The only product property is the zero product property.

Factoring is the process of breaking down a mathematical expression into its factors, which are individual parts that can be multiplied together to get the original expression. Factoring is often used in algebra to simplify expressions and solve equations.

For example:

Consider the expression x² + 5x + 6. This expression can be factored into (x + 2)(x + 3), where (x + 2) and (x + 3) are the factors. To check if this is correct, we can use the distributive property of multiplication and see that:
(x + 2)(x + 3) = x(x + 3) + 2(x + 3) = x^2 + 3x + 2x + 6 = x² + 5x + 6
Factoring can also be used to solve equations, by setting the expression equal to zero and then factoring to find the values of x that make the expression equal zero. For example, consider the equation x² + 5x + 6 = 0. We can factor the left side of the equation as (x + 2)(x + 3) = 0, and then use the zero product property to find that x = -2 or x = -3 are the solutions to the equation.