Introduction: Ratios & Proportions | Quantitative Reasoning for UCAT PDF Download

Ratio
- When comparing any two numbers, sometimes, it is necessary to find out how many times one number is greater (or less) than the other. In other words, we often need to express one number as a fraction of the other.
- The ratio of any number of quantities is expressed after removing any common factors that ALL the terms of the ratio have. For example, if there are two quantities having values of 4 and 2, their ratio is 4: 2, i.e., 2: 1 after taking the common factor 1 between them out.
Properties
- If two quantities whose values are A and B respectively are in the ratio a : b, since we know that some common factor k(>0) would have been removed from A and B to get the ratio a: b, we can write the original values of the two quantities (i.e., A and B) as ak and bk respectively.
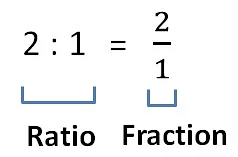
Example: If the salaries of two persons are in the ratio 7: 5, we can write their individual salaries as 7k and 5k respectively. - A ratio a: b can also be expressed as a/b. So if two items are in the ratio 2 : 3, we can say that their ratio is 2/3. If two terms are in the ratio 2, it means that they are in the ratio of 2/1, i.e., 2: 1.
- "A ratio is said to be a ratio of greater or less inequality or of equality according to as antecedent is greater than, less than or equal to consequent".
In other words:
(i) The ratio a: b where a > b is called a ratio of greater inequality (example 3: 2)
(ii) The ratio a: b where a < b is called a ratio of less inequality (example 3: 5)
(iii) The ratio a: b where a = b is called a ratio of equality (example 1: 1)
From this, we can find that a ratio of greater inequality is diminished and a ratio of less inequality is increased by adding the same quantity to both terms, i.e., in the ratio a : b.
- When we add the same quantity x (positive) to both the terms of the ratio, we have the following results:
(i) if a < b then (a + x) : (b + x) > a : b
(ii) if a > b then (a + x) : (b + x) < a : b
(iii) if a = b then (a + x) : (b + x) = a : b
Types of Problems in Ratios
Type - 1: As a bridge between 3 or more quantities
- Suppose you have a ratio relationship given between the salaries of two individuals A and B. Further, if there is another ratio relationship between B and C. Then, by combining the two ratios, you can come up with a single consolidated ratio between A, B and C. This ratio will give you the relationship between A and C.
Example 1: The Ratio of A’s salary to B’s salary is 2:3. The ratio of B’s salary to C’s salary is 4:5. What is the ratio of A’s salary to C’s salary?
Using the conventional process in this case:
- Take the LCM of 3 and 4 (the two values representing B’s amount). The LCM is 12.
- Convert B’s value in each ratio to 12.
- Thus, Ratio 1 = 8/12 and Ratio 2 = 12/15
- Thus, A:B:C = 8:12:15 Hence, A:C = 8:15
- Further, if it were given that A's salary was 800, you could derive the values of C's salary (as 1500).
Shortcut for this Process:
- The LCM process gets very cumbersome, especially if you are trying to create a bridge between more than 3 quantities.
- Suppose, you have the ratio train as follows: A:B = 2:3 B:C = 4:5 C:D = 6:11 D:E = 12:17
- In order to create one consolidated ratio for this situation, using the LCM process becomes too long.
- The shortcut goes as follows:
A : B : C : D : E can be written directly as:
2 * 4 * 6 * 12 : 3 * 4 * 6 * 12 : 3 * 5 * 6 * 12 : 3 * 5 * 11 * 12 : 3 * 5 * 11 * 17
Type- 2: Ratio as a Multiplier
- The moment we say that the ratio of two numbers A and B is 5: 1, what we mean to say that A is 5 times B.
- It can also be seen that A: B: C in A/2: B/3: C/4 = K is not the same as A: B: C = 1/2: 1/3: 1/4 since the multiplier of A, B and C are not the same in both the cases.
- Ratio of A : B : C in A/2 : B/3 : C/4 = K can be calculated in the following way Since A/2 = B/3 = C/4 = K,
so, A= 2K, B = 3K and C = 4 K
Hence, the ratio of A:B:C = 2:3:4.
While calculating the ratio of A, B and C in A: B: C = 1/2: 1/3: 1/4, we will multiply each of A, B and C by the LCM of the denominator of all the ratios, i.e., 12.
So, A : B : C = 6 : 4 : 3
Example 2: 10 persons can cut 8 trees in 12 days. How many days will 8 persons take to cut 6 trees?
- Let us see this question from a changed perspective.
- Suppose if the question is: 10 persons can cut 8 trees in 12 days. How many days will 10 persons take to cut 4 trees?
- The answer to this question is: Since the amount of work is getting halved, so the number of days will also get halved.
There are three factors, namely:
(i) The number of men
(ii) The number of days
(iii) The number of trees
which are responsible for the final answer.- Since the number of men is less in the final situation, so more days will be required.
- Hence, multiplier = 10/8 (had there been 12 persons, the multiplier would have been 10/12.)
- The number of trees is less in the final situation, so fewer number of days will be required. So, multiplier = 6/8
- Hence, the total number of days = 12 x 10/8 x 6/8 = 90/8 = 11.25 days
Example 3: Two numbers are in the ratio 3: 4. What part of the larger number must be added to each number so that their ratio becomes 5: 6?
- Let the two numbers be 3x and 4x.
- 3x + k/4x + k = 5/6
- 18x + 6k = 20x + 5k
- k = 2x
- ∴ Half of the larger number must be added to each number.
Example 4: There are 2 classes A and B. If 10 students leave class A and join class B, then the ratio of the number of students in class A and class B would reverse. Find the difference in the numbers of students in class A and class B.
- Let the numbers of students in class A and class B be ax and bx, respectively.
- Given:
⇒ ax - 10/bx + 10 = b/a
⇒ a2x − 10a = b2x + 10b
⇒ a2x – b2x – 10a – 10b = 0
⇒ (ax – bx – 10) (a + b) = 0- ∴ ax – bx = 10
- The difference in the number of students in class A and class B is 10.
|
31 videos|37 docs|23 tests
|





















