Measurement Units | Physics for EmSAT Achieve PDF Download

Introduction

• A physical quantity refers to something that can be assessed, and when conducting measurements, it is necessary to specify the unit being used in order to comprehend the magnitude of the measurement.
• To illustrate, distance can be quantified in either kilometers or miles. Although they are similar, they are not identical, and it is crucial to indicate the unit used for the measurement to accurately determine the distance.
• The international standard for units employed by scientists worldwide is known as the International System of Units, or SI units. 

It is important to bear in mind the six fundamental or base units of measurement within this system:

• Meter (m) - unit for measuring length
• Kilogram (kg) - unit for measuring mass
• Second (s) - unit for measuring time
• Ampere (A) - unit for measuring electrical current
• Kelvin (K) - unit for measuring temperature
• Mole (mol) - unit for measuring the amount of substance

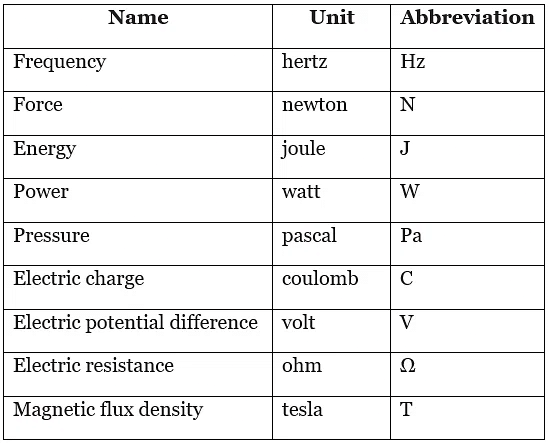
In addition to the fundamental units, there exist derived units. These derived units are derived from the fundamental units and are highly beneficial when expressing measurements, although they are not considered fundamental in themselves.

For instance, frequency represents the number of occurrences within a specific time period. While it is a valuable quantity, it is derived by dividing the unit of time. The standard unit for frequency is the hertz (Hz), which signifies "per second," originating from the fundamental unit of time, the second.

Derived units encompass

Sometimes, when using the standard SI unit, a measurement may yield a very large or very small number that is impractical to write out in its entirety. To address this, mathematicians employ a system known as standard form, which allows for the representation of large numbers in a condensed format.

This involves expressing the significant digits of the number as a value between 1 and 10, followed by multiplying it by a power of ten to restore its original magnitude.

For instance, the distances from the Sun to Pluto can be expressed as follows:

4,400,000,000,000 m = 4.4 × 10¹² m

and

7,300,000,000,000 m = 7.3 × 10¹² m

Unit prefixes

Another method to handle excessively long numerical measurements is by utilizing unit prefixes, which employ a standardized set of abbreviations to simplify the representation of numbers. For instance, instead of writing "1,000 meters," scientists would use "1 km."

Here are some commonly used prefixes and their corresponding powers of ten:

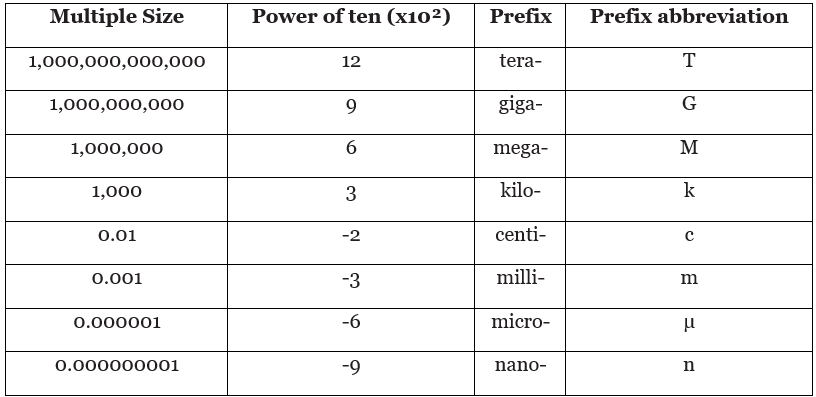
Using these prefixes, the distances from the Sun to Pluto can be expressed as:

4,400,000,000,000 m = 4.4 × 10¹² m = 4.4 terametres = 4.4 Tm

and

7,300,000,000,000 m = 7.3 × 10¹² m = 7.3 terametres = 7.3 Tm

Solved Examples

Ex.1: Which is larger: 360 kV or 3.6 MV?

360 kV = 360,000 volts

3.6 MV = 3,600,000 volts

So 3.6 MV is larger.

Unit conversion

Conversion of units can be beneficial to facilitate the utilization or comprehension of a quantity expressed in a different unit. The magnitude of the measurement remains the same throughout the conversion process.

When converting a measurement that includes prefixes back to standard form, it becomes necessary for performing calculations.

Example

Consider the calculation of electrical power when a 50 mA current flows through a 230 V light bulb.

The standard unit for electrical power is watts (W). To calculate electrical power, multiply the current by the voltage. The resulting value will be in watts if the current is measured in amperes and the voltage in volts.

In this case, the current is 50 mA, which can be converted to 0.05 A.

Power = Current × Voltage = 0.05 A × 230 V = 11.5 W

Question

To determine the power when a 12 mV LED experiences a current of 0.02 A, we need to convert the voltage to standard form.

The voltage is 12 mV, which can be converted to 0.012 V.

Power = Current × Voltage = 0.02 A × 0.012 V = 2.4 × 10^-4 W = 0.24 mW

In some instances, measurements may be provided in non-SI units and require conversion to their SI equivalents for practical use. An example of this arises when time is given in hours but needs to be expressed in seconds for a calculation.

Consider the calculation of electrical energy transferred by a 35 W light bulb when it remains illuminated for four hours.

The standard unit for energy is joules (J). Energy is determined by multiplying power by time. The result will be in joules if the power is measured in watts and the time in seconds.

To convert four hours to seconds, we multiply by the conversion factors:

1 hour = 60 minutes × 60 seconds = 3,600 s
Time = 4 hours × 3,600 s/hour = 14,400 s
Energy = Power × Time = 35 W × 14,400 s = 504,000 J = 504 kJ

Significant Figures

Significant figures refer to the limitations on accuracy when making measurements in physics. Sometimes it is more practical to express measurements with less detail. On the NASA website, the range of distances from the Sun to Pluto is provided as follows:

4,436,820,000,000 m to 7,315,930,000,000 m.

To simplify these numbers and remove unnecessary details, scientists round them off. This process, known as using significant figures, involves rounding the number to the level of detail that is most relevant.

The number of significant figures used corresponds to the digits considered important during the rounding process. For instance, the closest distance to Pluto may vary over time, resulting in different values for each orbit. To provide an approximate value for the distance from the Sun to Pluto, an astronomer might calculate the average of the closest and furthest distances.

The exact average is 5,876,375,000,000 m, but due to the variations in distance, it is reasonable to approximate this value. For example, the astronomer might state it as 5,900,000,000,000 m or even further approximate it as 6 terameters (Tm).

The average distance from the Sun to Pluto can be expressed in different levels of detail:

• 5,876,400,000,000 m to five significant figures (s.f.)
• 5,900,000,000,000 m to two s.f.
• 6 Tm to one s.f.

For example, if we want to determine the furthest distance from the Sun to Pluto with three significant figures:

• According to the NASA website, the distance is 7,315,930,000,000 m.
• Rounding this off to three significant figures gives us 7,320,000,000,000 m.

Question

To two significant figures, what is the closest distance from Pluto to the Sun?

According to the NASA website, the distance is 4,436,820,000,000 m, which can be rounded to 4,400,000,000,000 m (2 s.f.).

Significant Figures with Decimals:

The number of significant figures (s.f.) corresponds to the digits that are relevant when rounding a number to maintain its value. When dealing with decimal numbers, leading zeros before the first non-zero digit can be disregarded when counting significant figures. However, trailing zeros after the last non-zero digit are considered significant.

For example:

• The number 4.76000 has three significant figures.
• The number 0.0000476 also has three significant figures.
• In decimal numbers, trailing zeros are important and counted as significant figures. Thus, 0.00006100 has four significant figures, including the six, the one, and the two trailing zeros.

Question

If the value is 0.00206392 mol and needs to be rounded to four significant figures, the result would be 0.002064 mol (4 s.f.). When quoting the value of 0.00246392 amps to five significant figures, what is the result?

When rounding to five significant figures, ignoring the leading zeros, the value would be 0.0024639 A (5 s.f.).