Patterns Chapter Notes | Science Olympiad Class 4 PDF Download
| Table of contents |

|
| Patterns |

|
| Definition of Patterns |

|
| Number Pattern |

|
| Arithmetic Pattern |

|
| Geometric Pattern |

|
| Fibonacci Pattern |

|
| Rules for Patterns |

|
| Types of Patterns |

|
Patterns
The field of mathematics encompasses the study of numbers and the various patterns in which they can be arranged. Patterns in mathematics come in different forms, including number patterns, image patterns, logic patterns, word patterns, and more. Among these, number patterns are the most commonly encountered ones, as students are familiar with concepts like even numbers, odd numbers, skip counting, etc., which aid in comprehending these patterns easily.
Definition of Patterns
Patterns refer to a series or sequence that typically repeats itself. Patterns manifest in our everyday lives through colors, actions, shapes, numbers, and so on. They can be associated with any event or object and can be finite or infinite. In mathematics, patterns consist of a set of numbers arranged in a sequence that adheres to a specific rule. These rules establish a method for calculating or solving problems. For instance, in the sequence 3, 6, 9, 12, _, each number increases by 3. Thus, according to the pattern, the missing number would be 12 + 3 = 15.
The diagram below illustrates the various types of patterns and sequences that can be formed with numbers.
Different Types of Number Patterns
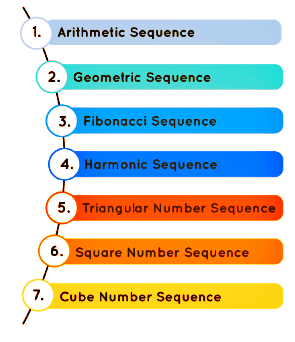
Number Pattern
Number patterns are the most prevalent type of patterns in mathematics, where a list of numbers follows a particular sequence based on a rule. The different types of number patterns include algebraic or arithmetic patterns, geometric patterns, and the Fibonacci pattern.
Arithmetic Pattern
Arithmetic patterns, also known as algebraic patterns, are sequences of numbers based on addition or subtraction, resulting in a sequence of related numbers. Given two or more numbers in a sequence, we can utilize addition or subtraction to identify the arithmetic pattern. Addition or subtraction can also be employed to determine missing numbers in a given sequence.
For instance, let's find the missing numbers in the series: 4, 8, ___, 16, 20, ___.
In the above pattern, we observe that each number increases by 4. Hence, the rule governing this pattern is adding 4 to the previous term to obtain the next term. By employing this pattern, we can find the missing numbers. Therefore, the missing numbers are 8 + 4 = 12 and 20 + 4 = 24.
Geometric Pattern
Geometric patterns are sequences of numbers that are based on multiplication and division. If two or more numbers in the sequence are provided, we can easily identify the unknown numbers in the pattern using multiplication and division operations. For example: 6, 18, 54, __, 486, __.
In the given series, we observe that each number is obtained by multiplying 3 with the previous number. Consequently, we can determine the missing numbers using this rule. Hence, the missing numbers are 54 × 3 = 162 and 486 × 3 = 1458.
Fibonacci Pattern
The Fibonacci pattern is a sequence of numbers in which each number is obtained by adding the two previous numbers together. The sequence begins with 0 and 1. Consider the Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, and so on. Here, we can observe that the pattern followed is: 0 + 1 = 1, 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8.
Rules for Patterns
To establish a complete pattern, certain rules need to be considered. Applying the rule requires understanding the nature of the sequence and the difference between two successive numbers. Some amount of guesswork and verification is necessary to ensure that the rule holds true for the entire series.
There are two basic categories for finding rules in number patterns:
- Ascending Order: When the numbers in the given pattern increase, they are said to be in an ascending order. These patterns usually involve addition or multiplication.
- Descending Order: When the numbers in the given pattern decrease, they are said to be in a descending order. These patterns typically involve subtraction or division.
Let's understand this with an example:
Example: Find the pattern rule for the series: 81, 27, 9.
- The first observation is that it is a descending pattern.
- So, let's start with the smallest number, 9. What can be done to 9 to obtain 27? We notice that 9 × 3 = 27.
- Now, let's check if this pattern holds for the next number. 27 × 3 = 81.
- Based on this observation, if we interpret the series in the given order, we can deduce that the pattern rule being followed is "Divide by 3."
- This implies that if we divide 81 by 3, we get 27, and when we divide 27 by 3, we get 9.
Likewise, we can determine the pattern rules for any given series of numbers.
Types of Patterns
There are three common types of patterns in mathematics:
- Repeating Pattern: A pattern that repeats over and over again in a sequence of numbers is called a repeating pattern.
- Growing Pattern: If the numbers or objects are arranged in an increasing order in a sequence, that pattern is referred to as a growing pattern.
- Shrinking Pattern: A shrinking pattern is a pattern where numbers or objects are arranged in a decreasing order.
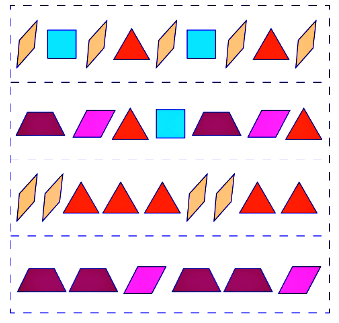
The figure below illustrates a repeating pattern of shapes.
|
53 videos|44 docs|59 tests
|

|
Explore Courses for Class 4 exam
|

|

















