Geometry Chapter Notes | Mathematics Olympiad Class 4 PDF Download
| Table of contents |

|
| Introduction |

|
| What are Geometric Shapes? |

|
| Building Blocks: What Makes Up a Shape? |

|
| Types of Lines |

|
| Closed vs. Open |

|
| Polygons |

|
| Solid Shapes |

|
| Symmetry: When Things Are Balanced |

|
Introduction
Imagine the world around you. You see squares on windows, circles on pizzas, and triangles on slices of cake (yum!). These, my friend, are all geometric shapes. In short, geometry is like a detective game where we analyze the shapes and sizes of things.
What are Geometric Shapes?
Think of a geometric shape as a flat outline, like a cookie cutter. It has a definite form and can be made up of straight lines, curves, or a combination of both. Shapes don't have thickness or depth, kind of like pictures on a flat piece of paper.
Building Blocks: What Makes Up a Shape?
Shapes are like Legos – they're built from smaller components! Here's the breakdown:
Point
- A dot represents an exact location in space with no length or breadth.
- Represented with capital letters (e.g., Point A).

Line Segment
- A straight path between two endpoints (e.g., line segment AB).

Line
- Imagine a straight path that goes on forever in one direction, like a ruler or the path of an ant marching on a straight sidewalk.
- These are lines! Lines are the basic building blocks of many shapes in geometry.

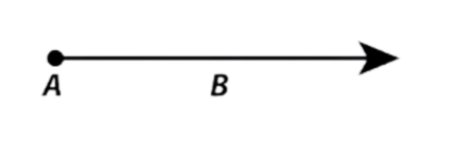
Ray
- A straight path starting from one endpoint and extending infinitely in one direction (e.g., ray AB).
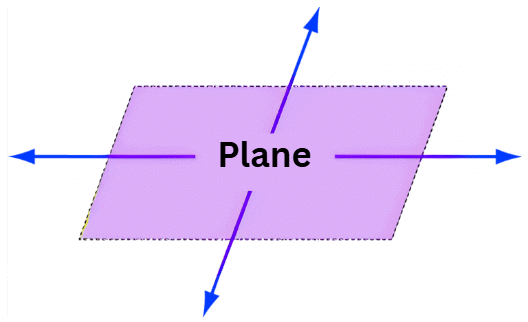
Plane
- A flat surface extending infinitely in all directions. Represented using three points (e.g., Plane PQR).
Curves
- Unlike straight lines, these bend and turn. The rainbow is a beautiful example of a curve.

Types of Lines
Parallel Lines
- Lines that never intersect and are always equidistant. Denoted as "parallel to".
- Imagine two train tracks running side-by-side. These are parallel lines. No matter how far you extend them, they will never meet.

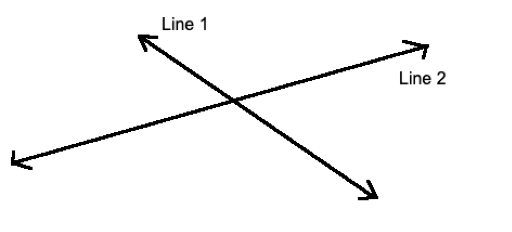
Intersecting Lines
- Lines that cross at a point.
- Example: The letter "X".
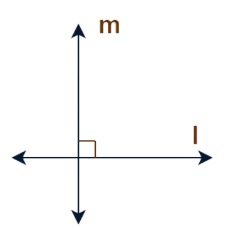
Perpendicular Lines
- Intersecting lines that meet at a right angle (90 degrees). Denoted as "perpendicular to".
Coinciding Lines: Perfect Overlap
- Imagine placing one ruler exactly on top of another ruler. These are coinciding lines.
- They are not just parallel, they completely overlap each other.
- They are like twins – you can't tell them apart!
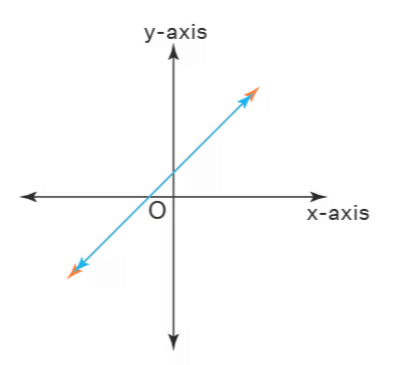 Coincident Lines
Coincident Lines
Closed vs. Open
Shapes come in two flavors: closed and open. Let's see the difference:
Closed Figures/Curves: Imagine a shape with a complete boundary, like a fence enclosing a yard. You can trace its outline without lifting your finger and end up exactly where you started. Circles, squares, and triangles are all examples of closed figures/curves.

Open Figures/Curves: These shapes are like paths that go on forever in one or both directions. Imagine an arrow – it has a starting point but no real endpoint. An open curve could also bend and turn like a spiral staircase. Examples include lines, rays (think of a laser beam!), and parabolas (the path a thrown object follows).

Polygons
Polygons are like the shape squad in geometry class. They're a special group of flat, closed shapes with straight sides. But how do we tell these guys apart? Here's your guide to identifying different types of polygons: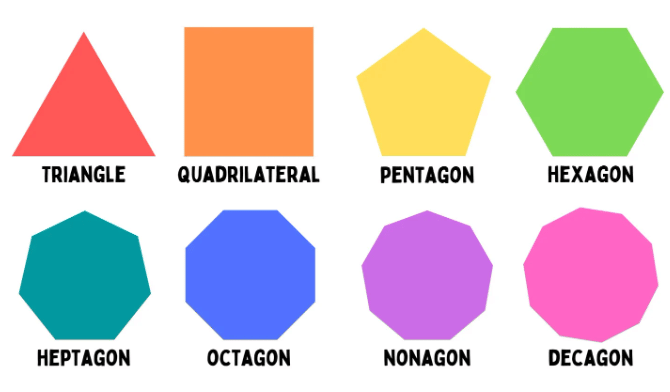
It has the following key components:
- Sides
- The straight line segments that form the boundary of the polygon.
- Example: A triangle has 3 sides, while a square has 4 sides.
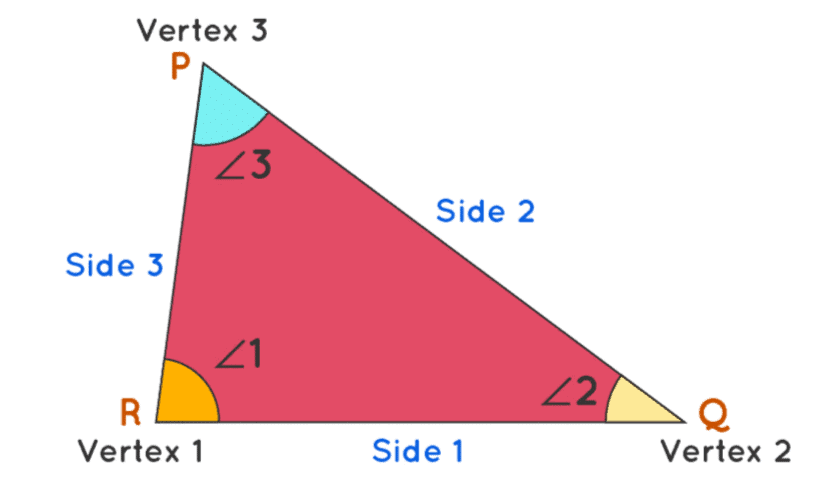
- Vertices (Singular: Vertex)
- The points where two sides meet.
- Example: A pentagon has 5 vertices, one at the meeting point of each pair of sides.
- Angles
- The space between two sides that meet at a vertex.
- Example: A square has 4 right angles (each 90 degrees).
- Diagonals
- Line segments that connect two non-adjacent vertices inside the polygon.
- Example: A rectangle has 2 diagonals.
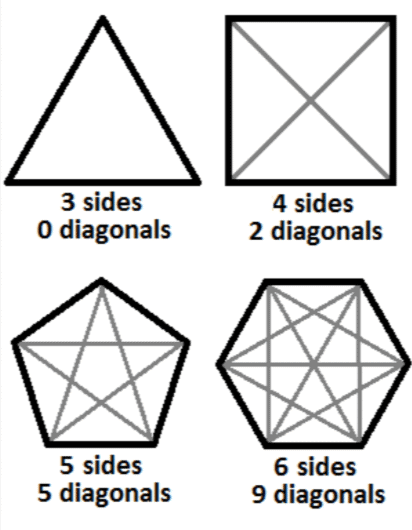
Different Types of Shapes
There are many cool shapes in the world of geometry, but let's focus on some of the most popular ones:
Circle: This champion has no corners and goes round and round forever (well, almost!). Imagine a pizza – that's a perfect circle!
Square: This dude is all about right angles (90 degrees) and equal sides. Think of a Rubik's cube – each side is a perfect square.
Rectangle: Similar to a square, this guy has four straight sides and opposite sides that are equal in length. But unlike a square, its corners aren't always right angles. Your notebook paper is a rectangle!
Triangle: The three-legged wonder! A triangle always has three sides and three angles that add up to 180 degrees. Traffic signs and slices of bread are common triangle examples.
There are more shapes, Let's learn about them:
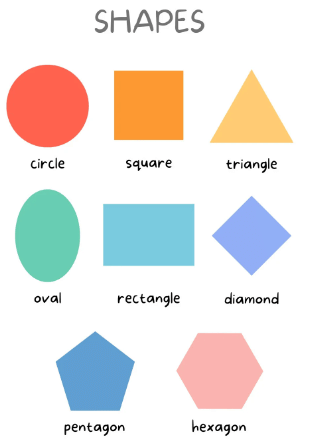
The Big Question: How Many Sides Do You Have?
The number of sides is the key to identifying polygons. Here are some common ones:
Triangle: These sharp characters have 3 sides and 3 angles (remember, their angles always add up to 180 degrees!).
Quadrilateral: Fancy word for a 4-sided polygon. Think of a rectangle, square, or kite.
Pentagon: This pen pal has 5 sides, like a high-five!
Hexagon: The busy bee of shapes with 6 sides, like a honeycomb.
1. Rectangle: The Organized One
Sides: 4 straight sides.
Angles: All 4 corners are right angles (90 degrees).
Special Feature: Opposite sides are always equal in length. Imagine a rectangle as a perfectly organized room – everything has its place!
2. Square: The Super Rectangle
Think of it as a rectangle that went to the gym and got all its sides equal. It has 4 sides, all the same length, and all corners are right angles.
Basically a super organized rectangle!
3. Equilateral Triangle: The All-Equal Star
This triangle is the champion of equality. All 3 sides are the same length, and all 3 angles are also equal (each measuring 60 degrees). Imagine a perfect pizza slice – that's an equilateral triangle!
4. Scalene Triangle: The Rebel
This is the free spirit of triangles. All 3 sides and all 3 angles are different lengths and measures. There are no equal sides or angles here!
5. Isosceles Triangle: The Two-Timer
This triangle likes to play favorites. It has 2 sides that are equal in length (the base can be different). The angles opposite the equal sides are also equal. Think of a roof – that's often an isosceles triangle!
Arc
An arc is a curved line that forms a part of a circle. It's like a slice of a pizza, but instead of a straight line cut, it's a curved cut. Unlike polygons with straight sides, arcs have a curved boundary.
Solid Shapes
A net is like a blueprint for a 3D shape. Imagine cutting out flat pieces of cardboard with tabs, then folding and gluing them together to form a box. The flat pieces together make up the net.
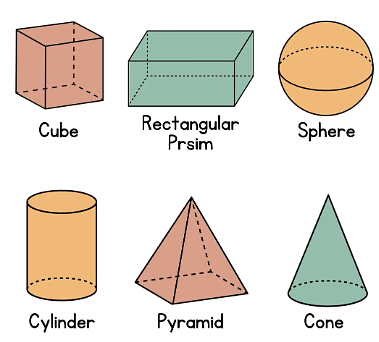
Here's how to identify the solid from the net:
Look for matching shapes and sizes. Pieces that fit together along edges likely connect in the 3D shape.
Identify tabs. These are small flaps meant to be folded and glued to other parts of the net.
Consider the overall shape formed by the net pieces. Does it resemble a cube, pyramid, cylinder, or something else?
By analyzing the pieces, tabs, and overall form, you can become a net detective and identify the hidden 3D shape!
Symmetry: When Things Are Balanced
Symmetry is all about balance and matching parts. Imagine folding a paper butterfly in half. The two halves are symmetrical. They are mirror images of each other, like twins facing each other. There are different types of symmetry: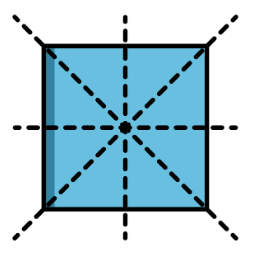
Line Symmetry: This is the kind of symmetry we saw with the butterfly. Fold it in half, and both sides match perfectly, like a mirror reflection.
Rotational Symmetry: Imagine a pizza with pepperoni slices. If you rotate the pizza, the pattern of pepperoni keeps repeating. This is rotational symmetry.
Symmetry is everywhere in the world around us, from the butterfly's wings to the snowflakes falling from the sky.
|
33 videos|96 docs|46 tests
|
FAQs on Geometry Chapter Notes - Mathematics Olympiad Class 4
| 1. What are geometric shapes and why are they important in geometry? |  |
| 2. What is the difference between closed and open shapes? |  |
| 3. How do you calculate the perimeter of a polygon? |  |
| 4. What are solid shapes, and how do they differ from flat shapes? |  |
| 5. What is symmetry, and how can we identify it in shapes? |  |




















