Kinetic Energy: Types, Examples and Formula | AP Physics 1 - Grade 9 PDF Download
| Table of contents |

|
| Introduction |

|
| Kinetic Energy Examples |

|
| Transformation of Kinetic Energy |

|
| Kinetic Energy Formula |

|
| Deriving Kinetic Energy Formula |

|
| Various Forms of Kinetic Energy |

|
Introduction
Kinetic energy, a fundamental concept in physics, refers to the energy transferred to an object due to its motion. To put an object in motion, force is applied, requiring the performance of work. This work leads to energy transfer, resulting in the object moving at a new speed. The transferred energy is termed kinetic energy and is determined by the object's mass and the speed it attains.
- In the realm of physics, the kinetic energy of an object signifies the work it can accomplish through its motion. It is crucial to note that kinetic energy is a scalar quantity, representing solely its magnitude without any directional component.
- In summary, kinetic energy is the energy associated with the motion of an object, acquired by applying work to it. It relies on both the object's mass and the square of its speed, playing a crucial role in understanding various physical phenomena.
 Kinetic Energy
Kinetic Energy
Units of Kinetic Energy
Understanding and quantifying kinetic energy require familiarity with its units. In the International System of Units (SI), the standard unit for kinetic energy is the Joule (J). One Joule is equivalent to 1 kilogram-meter squared per second squared (kg·m²/s²). This unit denotes the kinetic energy possessed by an object with a mass of 1 kilogram moving at a velocity of 1 meter per second.

In the CGS system (centimeter-gram-second), the unit of kinetic energy is the erg. An erg is defined as the kinetic energy possessed by an object with a mass of 1 gram moving at a velocity of 1 centimeter per second.
Both the Joule and erg are derived from fundamental units of mass, length, and time, providing a standardized means to express and compare kinetic energy across different measurement systems.
Kinetic Energy Examples
- The kinetic energy of a river is evident as it flows at a specific speed, possessing both velocity and mass.
- As an asteroid descends towards Earth, it exhibits an immense amount of kinetic energy due to its high velocity and substantial mass.
- During flight, an airplane attains higher kinetic energy owing to its considerable mass and rapid velocity.
- When a person walks, their legs and body in motion result in the acquisition of kinetic energy.
- As a thrown ball moves through the air, it gains kinetic energy, the amount of which is determined by its throwing speed.
- Objects falling towards the ground amass kinetic energy as a result of the force of gravity, with the impact's kinetic energy directly proportional to the object's mass and velocity.
- A truck traveling at the same speed as a car possesses greater kinetic energy due to its significantly higher mass.
 Kinetic Energy Examples
Kinetic Energy Examples
Transformation of Kinetic Energy
- Elastic Collision: During collisions between objects like billiard balls, kinetic energy can be transferred. When the balls collide and rebound, some of the kinetic energy transforms into other forms, such as heat and sound energy.
- Pendulum Swing: As a pendulum swings back and forth, it continually converts between potential and kinetic energy. At the highest point of the swing, potential energy is dominant, while descending converts potential energy into kinetic energy.
- Car Braking: When a car applies its brakes, the kinetic energy of the moving vehicle transforms into other forms, primarily heat energy. Friction between the brake pads and wheels slows down the car by converting kinetic energy into thermal energy.
- Wind Turbine: In a wind turbine, the kinetic energy of moving air is captured and converted into electrical energy. As the wind blows, it rotates the turbine blades, transforming the wind's kinetic energy into mechanical energy, which then drives a generator to produce electricity.
- Waterfall: As water falls from a higher elevation in a waterfall, its potential energy gradually converts into kinetic energy. Gravity causes the flowing water to gain speed and kinetic energy, which can be harnessed to generate hydroelectric power.
- Yo-Yo Transformation: A yo-yo demonstrates the transformation of kinetic energy. Initially at rest in a person's hand, the yo-yo stores energy as potential energy. When released, gravity pulls the yo-yo downward, converting potential energy into kinetic energy. The yo-yo ball accelerates, gaining speed and kinetic energy. At the bottom of its path, the energy is entirely in the form of kinetic energy.
However, the transformation continues. As the yo-yo reaches the end of its descent, it starts climbing back up due to the tension in the string. The kinetic energy of the yo-yo ball begins converting back into potential energy as it gains height. This process repeats as the yo-yo moves up and down, with continuous conversions between potential and kinetic energy.
Kinetic Energy Formula
The formula of kinetic energy is an essential tool in understanding the energy associated with an object’s motion. The equation for kinetic energy is given by:
KE = 1/2 mv2
The equation above represents the kinetic energy (KE) of an object, where "m" represents the mass and "v" represents the velocity.
 According to this equation, kinetic energy is directly proportional to both the mass and the square of the velocity of the object. This means that an increase in either the mass or the velocity will result in an increase in the kinetic energy. It is important to note the significance of the relationship between kinetic energy and velocity, as the velocity term is squared in the equation. This implies that even small changes in velocity can have a substantial impact on the object's kinetic energy.To calculate the kinetic energy of an object using this equation, you need to know the mass and velocity of the object. First, square the velocity, and then multiply it by half of the object's mass. The resulting value will give you the kinetic energy of the object.
According to this equation, kinetic energy is directly proportional to both the mass and the square of the velocity of the object. This means that an increase in either the mass or the velocity will result in an increase in the kinetic energy. It is important to note the significance of the relationship between kinetic energy and velocity, as the velocity term is squared in the equation. This implies that even small changes in velocity can have a substantial impact on the object's kinetic energy.To calculate the kinetic energy of an object using this equation, you need to know the mass and velocity of the object. First, square the velocity, and then multiply it by half of the object's mass. The resulting value will give you the kinetic energy of the object.
Why is Kinetic Energy a Scalar Quantity?
Kinetic energy is considered a scalar quantity because it does not have an associated direction. It represents the magnitude of energy possessed by an object. While velocity, which is a vector quantity, includes both magnitude and direction, the calculation of kinetic energy only takes into account the magnitude of velocity. The kinetic energy depends on the mass and the square of the magnitude of velocity. By squaring the velocity term, kinetic energy is always positive, regardless of the direction of motion. Therefore, even though velocity is a vector quantity, the calculation of kinetic energy focuses solely on magnitude, resulting in it being a scalar quantity.
Deriving Kinetic Energy Formula
The formula for calculating kinetic energy is an essential tool in understanding the energy associated with an object’s motion. The equation for kinetic energy is given by:
KE = 1/2 mv2
To begin, let’s consider a particle of mass “m” moving with a velocity “v.” The kinetic energy of this particle can be defined as the work done to accelerate the particle from rest to its current velocity. According to the work-energy theorem, the work done on an object is equal to the change in its kinetic energy.
The work done on the particle is given by the equation:
Work = Force x distance
(i) In the case of constant force, the work done can be calculated as:
Work = Force x distance
Now, let’s express the force in terms of mass and acceleration. According to Newton’s second law of motion, force (F) is equal to mass (m) multiplied by acceleration (a). Since the particle is moving with a constant velocity, its acceleration is zero. Therefore, the force acting on the particle is zero.
Substituting the force into the work equation, we have:
Work = 0 x displacement
Work = 0
This means that no work is done on the particle as it moves with a constant velocity. Consequently, there is no change in its kinetic energy.
(ii) In the case when the particle is initially at rest and then accelerated to a final velocity “v” by an external force.
In this case, work is done on the particle to change its velocity.
The work done on the particle is equal to the change in its kinetic energy. So, we can write:
Work = Change in kinetic Energy
Using the work formula:
Work = Force x displacement
The force acting on the particle is equal to the mass of the particle (m) multiplied by its acceleration (a). Since the initial velocity is zero, the final velocity is “v,” and the displacement is “d,” we have:
Work = (m x α) x d
Now, recall that the formula for acceleration (α) is given by: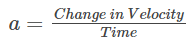
Since the initial velocity is zero, the change in velocity is “v” and the time taken is “t,” we can rewrite the equation as:
α = v/t
Substituting this back into the work equation, we have: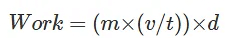
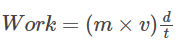
The quantity (d / t) represents the average velocity (vavg) of the particle. So, we can rewrite the equation as: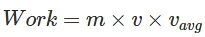
Now, the average velocity (vavg) is equal to half of the final velocity (v), as the particle starts from rest and reaches a final velocity “v.” Therefore, we can further simplify the equation as: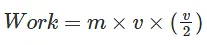
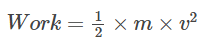
Finally, we equate the work done to the change in kinetic energy: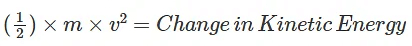
Hence, we have derived the equation for kinetic energy: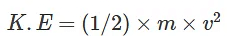
This equation relates the kinetic energy (K.E) of an object to its mass (m) and velocity (v). It demonstrates that the kinetic energy is directly proportional to the square of the velocity and the mass of the object.
Various Forms of Kinetic Energy
Kinetic energy manifests in different forms depending on the context. Here are some common types:
- Translational Kinetic Energy: This form of kinetic energy pertains to the energy associated with the linear motion of an object. It is most commonly observed when objects move along a straight path.
- Rotational Kinetic Energy: Objects that rotate or spin around an axis exhibit rotational kinetic energy. Examples include spinning tops, wheels, and rotating machinery.
- Vibrational Kinetic Energy: Vibrational kinetic energy arises from the oscillatory motion of particles within a system. It is observed in vibrating strings, molecules, or atoms undergoing vibrational movement.
- Thermal Kinetic Energy: Thermal kinetic energy is linked to the random motion of particles within a substance. It determines temperature and facilitates heat transfer. Higher thermal kinetic energy corresponds to faster particle movement.
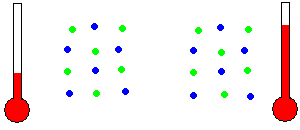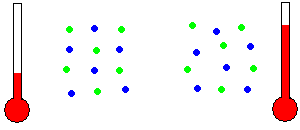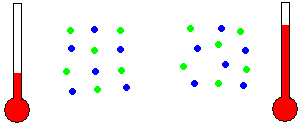
- Electrical Kinetic Energy: Electrical kinetic energy is associated with the movement of charged particles, such as electrons, in an electric current. It is employed in various electrical devices and serves as a means of energy transfer.
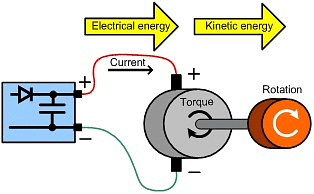
These diverse forms of kinetic energy illustrate the broad range of phenomena where energy is connected to the motion of objects or particles. Each type of kinetic energy possesses distinct characteristics and contributes to different areas of physics and everyday life.
|
48 videos|69 docs|30 tests
|
FAQs on Kinetic Energy: Types, Examples and Formula - AP Physics 1 - Grade 9
| 1. What is kinetic energy? |  |
| 2. What are some examples of kinetic energy? |  |
| 3. How is kinetic energy transformed? |  |
| 4. What is the formula for kinetic energy? |  |
| 5. How can the formula for kinetic energy be derived? |  |















