Tips and Tricks: Multiplication - 1 | Improve Your Calculations: Vedic Maths (English) - Class 6 PDF Download
| Table of contents |

|
| Introduction |

|
| Easy way for multiplication |

|
| Second Method |

|
| Vinculum |

|
Introduction
Multiplication in considered as one of the most difficult of the four mathematical operations. Students are scared of multiplication as well as tables. Just by knowing tables up to 5 students can multiply bigger numbers easily by some special multiplication methods of Vedic Mathematics. We should learn and encourage children to look at the special properties of each problem in order to understand it and decide the best way to solve the problem. In this way we also enhance the analytical ability of a child. Various methods of solving the questions /problems keep away the monotonous and charge up student’s mind to try new ways and in turn sharpen their brains.
Easy way for multiplication
Sutra: Vertically and Cross wise:
For speed and accuracy tables are considered to be very important. Also students think why to do lengthy calculations manually when we can do them faster by calculators. So friends/ teachers we have to take up this challenge and give our students something which is more interesting and also faster than a calculator. Of course it’s us (the teachers/parents) who do understand that more we use our brain, more alert and active we will be for, that is the only exercise we have for our brain.
Example 1: 7 x 8
Step 1: Here base is 10, 7 – 3 (7 is 3 below 10) also called deficiencies
× 8 – 2 (8 is 2 below 10) also called deficiencies
Step 2: Cross subtract to get first figure (or digit) of the answer: 7 – 2 = 5 or 8 – 3 = 5, the two difference are always same.
Step 3: Multiply vertically i.e. –3 × –2 = 6 which is second part of the answer.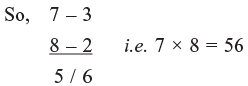
Example 2: To find 6 × 7
Step 1: Here base is 10,
6 – 4 (6 is 4 less than 10) i.e. deficiencies
7 – 3 (7 is 3 less than 10) i.e. deficiencies
Step 2: Cross subtraction : 6 – 3 = 3 or 7 – 4 = 3 (both same)
Step 3: – 3 × – 4 = + 12 , but 12 is 2 digit number so we carry this 1 over to 3 ( obtained in 2 step)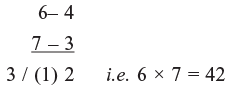
Second Method
Same Base Method
When both the numbers are more than the same base. This method is extension of the above method i.e. we are going to use same sutra here and applying it to larger numbers.
Example 1: 12 × 14
Step 1: Here base is 10
12 + 2 [12 is 2 more than 10 also called surplus]
14 + 4 [14 is 4 more than 10also called surplus]
Step 2: Cross add: 12 + 4 =16 or 14 + 2 = 16,(both same) which gives first part of answer = 16
Step 3: Vertical multiplication: 2 × 4 = 8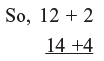
16 / 8 So, 12 × 14 = 168
(14 + 2 = 12 + 4)
Example 2: 105 x 107
Step 1: Here base is 100
105 + 05 [105 is 5 more than 100 or 5 is surplus]
107 + 07 [107 is 7 more than 100 or 7 is surplus]
Base here is 100 so we will write 05 in place of 5 and 07 in place of 7
Step 2: Cross add: 105 + 7 = 112 or 107 + 5 = 112 which gives first part of the answer = 112
Step 3: Vertical multiplication: 05 × 07 = 35 (two digits are allowed)
As the base in this problem is 100 so two digits are allowed in the second part.
So, 105 × 107 = 11235
Example 3: 112 x 115
Step 1: Here base is 100
112 + 12 [2 more than 100 i.e. 12 is surplus]
115 + 15 [15 more than 100 i.e. 15 is surplus]
Step 2: Cross add: 112 + 15 = 127 = 115 + 12 to get first part of answer i.e.127
Step 3: Vertical multiplication 12 × 15 = ? Oh, my god!It’s such a big number. How to get product of this? Again use the same method to get the product.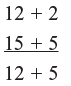
= 15 + 2 = 17/ (1) 0, 17 + 1 / 0 = 180 i.e. 12 × 15 = 180
But only two digits are allowed here, so 1 is added to 127 and we get (127 + 1) = 128
So, 112 × 115 = 128, 80
Both numbers less than the same base
Same sutra applied to bigger numbers which are less than the same base.
Example 1: 99 × 98
Step 1: Check the base: Here base is 100 so we are allowed to have two digits on the right hand side.
∴ 99 – 01 (1 less than 100 ) i.e. 01 deficiency
98 – 02 (2 less than 100) i.e. 0 2 deficiency
Step 2: Cross–subtract: 99 – 02 = 97 = 98 – 01 both same so first part of answer is 97
Step3: Multiply vertically – 01 × – 02 = 02 (As base is 100 so two digits are allowed in second part
So, 99 × 98 = 9702

11 + 2 = 13 = 12 + 1 / 1 × 2 = 12 so, 11 × 12 = (1) 32 as only two digits are allowed on right hand side so add 1to L.H.S.
So, L.H.S. = 77 + 1 = 78
Hence 89 × 88 = 7832
Example 3: 988 × 999
Step 1: As the numbers are near 1000 so the base here is 1000 and hence three digits allowed on the right hand side
988 – 012 (012 less than 1000) i.e. deficiency = 0 12
999 – 001 (001 less than 1000) i.e. deficiency = 00 1
Step 2: Cross – subtraction: 988 – 001 = 987 = 999 – 012 = 987
So first part of answer can be 987
Step 3: Multiply vertically: –012 xs – 001 = 012 (three digits allowed)
∴ 988 × 999 = 987012
How to check whether the solution is correct or not by 9 – check method:
Example 1: 99 × 98 = 9702 Using 9 – check method.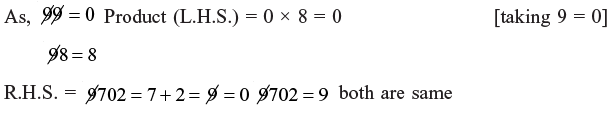
As both the sides are equal answer may be correct.
Example 2: 89 × 88 = 7832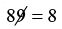
88 = 8 + 8 = 16 = 1 + 6 = 7 (add the digits)
L.H.S. = 8 × 7 = 56 = 5 + 6 = 11 = 2 (1 + 1)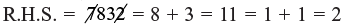
As both the sides are equal, so answer is correct
Example 3: 988 × 999 = 987012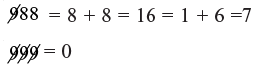
As 0 × 7 = 0 = LHS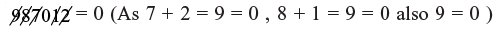
∴ RHS = 0
As LHS = RHS So, answer is correct.
Multiplying bigger numbers close to a base: (number less than base)
Example 1: 87798 x 99995
Step 1: Base here is 100000 so five digits are allowed in R.H.S.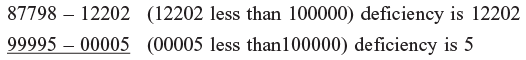
Step 2: Cross–subtraction: 87798 - 00005 = 87793
Also 99995 – 12202 = 87793 (both same)
So first part of answer can be 87793
Step 3: Multiply vertically: –12202 × – 00005 = + 61010
∴ 87798 × 99995 = 8779361010
Checking:
LHS = 3 x 5 = 15 total = 1 + 5 = 6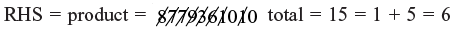
L.H.S = R.H.S. So, correct answer
Example 2: 88777 × 99997
Step 1: Base have is 100000 so five digits are allowed in R.H.S.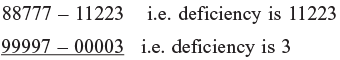
Step 2: Cross subtraction: 88777 – 00003 = 88774 = 99997 – 11223
So first part of answer is 88774
Step 3: Multiply vertically: – 11223 × – 00003 = + 33669
∴ 88777 × 99997 = 8877433669
Checking: 88777 total 8 + 8 + 7 + 7 + 7 = 37 = + 10 = 1
∴ LHS = 1 × 7 = 7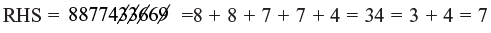
i.e. LHS = RHS So, correct answer
Example 3: 88777 × 99997
Step 1: Base have is 100000 so five digits are allowed in R.H.S.
88777 – 11223 i.e. deficiency is 11223
99997 – 00003 i.e. deficiency is 3
Step 2: Cross subtraction: 88777 – 00003 = 88774 = 99997 – 11223
So first part of answer is 88774
Step 3: Multiply vertically: – 11223 × – 00003 = + 33669
∴ 88777 × 99997 = 8877433669
Checking: 88777 total 8 + 8 + 7 + 7 + 7 = 37 = + 10 = 1
∴ LHS = 1 × 7 = 7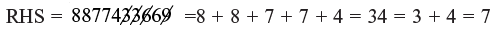
i.e. LHS = RHS So, correct answer
Multiply bigger number close to base (numbers more than base)
Example 1: 10021 × 10003
Step 1: Here base is 10000 so four digits are allowed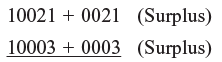
Step 2: Cross – addition 10021 + 0003 = 10024 = 10003 + 0021 (both same)
∴ First part of the answer may be 10024
Step 3: Multiply vertically: 10021 × 0003 = 0063 which form second part of the answer
∴ 10021 × 10002 = 100240063
Checking: 10021 = 1+ 2 + 1 + 1 = 4
10003 = 1 + 3 = 4
∴ LHS = 4 × 4 = 16 = 1 + 6 = 7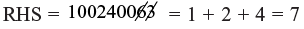
As LHS = RHS So, answer is correct
Example 2: 11123 × 10003
Step 1: Here base is 10000 so four digits are allowed in RHS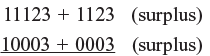
Step 2: Cross–addition: 11123 + 0003 = 11126 = 10003 + 1123 (both equal)
∴ First part of answer is 11126
Step 3: Multiply vertically: 1123 × 0003 = 3369 which form second part of answer
∴ 11123 × 10003 = 111263369
Checking:
11123 = 1 + 1 + 1 + 2 + 3 = 8
10003 = 1 + 3 = 4 and 4 × 8 = 32 = 3 + 2 = 5
∴ LHS = 5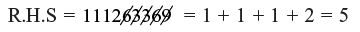
As L.H.S = R.H.S So, answer is correct
Numbers near different base: (Both numbers below base)
Example 1: 98 × 9
Step 1: 98 Here base is 100 deficiency = 02
9 Base is 10 deficiency = 1
∴ 98 – 02 Numbers of digits permitted on R.H.S is 1 (digits in lower base )
Step 2: Cross subtraction: 98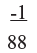
It is important to line the numbers as shown because 1 is not subtracted from 8 as usual but from 9 so as to get 88 as first part of answer.
Step 3: Vertical multiplication: (-02) x (-1) = 2 (one digits allowed )
∴ Second part = 2
∴ 98 × 9 = 882
Checking:
(Through 9 – check method)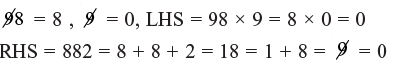
As LHS = RHS So, correct answer
Example 2: 993 × 97
Step 1: 993 base is 1000 and deficiency is 007
97 base is 100 and deficiency is 03
∴ 993 – 007 (digits in lower base = 2
So, 2 digits are permitted on
× 97 – 03 RHS or second part of answer)
Step 2: Cross subtraction: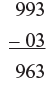
Again line the number as shown because 03 is subtracted from 99 and not from 93 so as to get 963 which from first part of the answer.
Step 3: Vertical multiplication: (–007) – (–03) = 21 only two digits are allowed in the second part of answer So, second part = 21
∴ 993 × 97 = 96321
Checking: (through 9 – check method)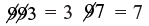
∴ L.H.S. = 3 × 7 = 21 = 2 + 1 = 3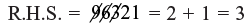
As LHS =RHS so, answer is correct
Example 3: 9996 base is 10000 and deficiency is 0004
988 base is 1000 and deficiency is 012
∴ 9996 – 0004 (digits in the lower base are 3 so, 3digits
× 988 – 012 permitted on RHS or second part of answer)
Step 2: Cross–subtraction: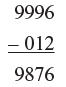
Well, again take care to line the numbers while subtraction so as to get 9876 as the first part of the answer.
Step 3: Vertical multiplication: (–0004) × (–012) = 048
(Remember, three digits are permitted in the second part i.e. second part of answer = 048
∴ 9996 × 988 = 9876048
Checking: (9 – check method)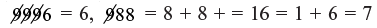
∴ LHS = 6 × 7 = 42 = 4 + 2 = 6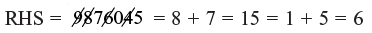
As, LHS =RHS so, answer is correct
When both the numbers are above base
Example 1: 105 × 12
Step 1: 105 base is 100 and surplus is 5
12 base is 10 and surplus is 2
∴ 105 + 05 (digits in the lower base is 1 so, 1 digit is permitted in the second part of answer )
12 + 2
Step 2: Cross–addition: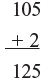
(again take care to line the numbers properly so as to get 125 )
∴ First part of answer may be 125
Step 3: Vertical multiplication: 05 × 2 = (1)0 but only 1 digit is permitted in the second part so 1 is shifted to first part and added to 125 so as to get 126
∴ 105 × 12 = 1260
Checking: 105 = 1 + 5 = 6 , 12 = 1 + 2 = 3
∴ LHS = 6 × 3 = 18 = 1 + 8 = 9 = 0
∴ RHS = 1260 = 1 + 2 + 6 = 9 = 0
Example 2: 1122 × 104
Step 1: 1122 – base is 1000 and surplus is 122
104 – base is 100 and surplus is 4
∴ 1122 + 122
104 + 04 (digits in lower base are 2 so, 2-digits are permitted in the second part of answer )
Step 2: Cross–addition
∴ First part of answer may be 1162
Step 3: Vertical multiplication: 122 × 04 = 4, 88
But only 2 – digits are permitted in the second part, so, 4 is shifted to first part and added to 1162 to get 1166 ( 1162 + 4 = 1166 )
∴ 1122 × 104 = 116688
Can be visualised as: 1122 + 122
104 + 04
1162 / ← (4) 88 = 116688
+ 4 /
Checking: 1122 = 1 + 1 + 2 + 2 + = 6, 104 = 1 + 4 =5
∴ LHS = 6 × 5 = 30 = 3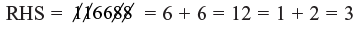
As LHS = RHS So, answer is correct
Example 3: 10007 × 1003
Now doing the question directly
10007 + 0007 base = 10000
× 1003 + 003 base = 1000
10037 / 021 (three digits per method in this part)
∴ 10007 × 10003 = 10037021
Checking: 10007 = 1 + 7 = 8 , 1003 = 1 + 3 = 4
∴ LHS = 8 × 4 = 32 = 3 + 2 = 5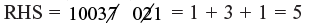
As LHS = RHS so, answer is correct
Vinculum
“Vinculum” is the minus sign put on top of a number e.g. 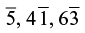 etc. which means (–5), (40 – 1) , (60 – 3) respectively
etc. which means (–5), (40 – 1) , (60 – 3) respectively
Advantages of using vinculum
- It gives us flexibility, we use the vinculum when it suits us .
- Large numbers like 6, 7, 8, 9 can be avoided.
- Figures tend to cancel each other or can be made to cancel.
- 0 and 1 occur twice as frequently as they otherwise would.
Converting from positive to negative form or from normal to vinculum form
Sutras: All from 9 the last from 10 and one more than the previous one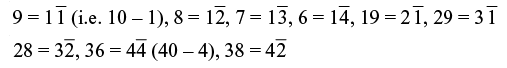
Steps to convert from positive to vinculum form
- Find out the digits that are to be converted i.e. 5 and above.
- Apply “all from 9 and last from 10” on those digits.
- To end the conversions “add one to the previous digit”.
- Repeat this as many times in the same number as necessary.
Numbers with several conversions

From vinculum back to normal form
Sutras: “All from 9 and last from ten” and “one less than then one before”.
Steps to convert from vinculum to positive form
- Find out the digits that are to be converted i.e. digits with a bar on top.
- Apply “all from 9 and the last from 10” on those digits
- To end the conversion apply “one less than the previous digit”
- Repeat this as many times in the same number as necessary
When one number is above and the other below the base
Example1: 102 × 97
Step 1: Here, base is 100
102 + 02 (02 above base i.e. 2 surplus)
97 – 03 (03 below base i.e. 3 deficiency)
Step 2: Divide the answer in two parts as 102 / + 02
97 / – 03
Step 3: Right hand side of the answer is (+ 02) × (– 03) = – 06 = 06
Step 4: Left hand side of the answer is 102 – 3 = 99 = 97 + 02 (same both ways)
∴ 102 × 97 = 9906 = 9894 (i.e. 9900 – 6 = 9894)
Checking: 102 = 1 + 2 = 3, 9 7 = 7
∴ L.H.S. = 3 × 7 = 21 = 1 + 2 = 3
∴ R.H.S = 9894 = 8 + 4 = 12 = 1 + 2 = 3
As L.H.S. = R.H.S. So, answer is correct
Example 2: 1002 × 997
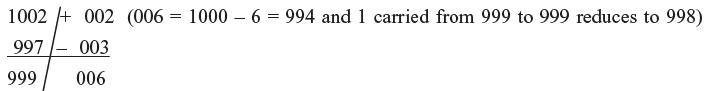
∴ 1002 × 997 = 998 994
When base is not same
Example 1: 988 × 12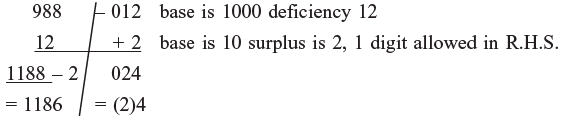
∴ 988 × 12 = 1186 4 = 11856 (because 4 = 10 – 4 = 6)
Checking: 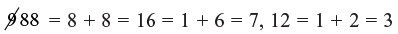
∴ LHS = 7 × 3 = 21 = 2 + 1 = 3
R.H.S = 11856 = 1 + 5 + 6 = 12 = 1 + 2 = 3
As LHS = RHS So, answer is correct
Example 2: 1012 × 98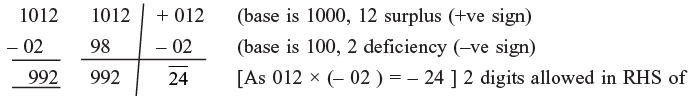
Ans:
∴ 1012 × 98 = 99224 = 99176 [ As 992200 – 24 = 99176]
Checking: 1012 = 1 + 1 + 2 = 4, 98 = 8
LHS = 4 × 8 = 32 = 3 + 2 = 5
RHS = 99176 = 1 + 7 + 6 = 14 = 1 + 4 = 5
As RHS = LHS so, answer is correct
|
38 videos|31 docs|9 tests
|















