Tips and Tricks: Square Roots | Improve Your Calculations: Vedic Maths (English) - Class 6 PDF Download
Square Roots: General method
As 12 = 1 22 = 4 32 = 9 42 = 1[ 6 ] 52 = 2 [5] 62 = 3 [6]
72 = 4 [9] 82 = 6 [4] 92 = 8[1] i.e. square numbers only have digits 1, 4, 5, 6, 9, 0 at the units place (or at the end)
Also in 16, digit sum = 1 + 6 = 7, 25 = 2 + 5 = 7, 36 = 3 + 6 = 9, 49 = 4 + 9 = 13
13 = 1 + 3 = 4, 64 = 6 + 4 = 10 = 1 + 0 = 1, 81 = 8 + 1 = 9 i.e. square number only have digit sums of 1, 4, 7 and 9.
This means that square numbers cannot have certain digit sums and they cannot end with certain figures (or digits) using above information which of the following are not square numbers:
(1) 4539 (2) 6889 (3) 104976 (4) 27478 (5) 12345
Note: If a number has a valid digit sum and a valid last figure that does not mean that it is a square number. If 75379 is not a perfect square in spite of the fact that its digit sum is 4 and last figure is 9.
Square Root of Perfect Squares
Example 1: √5184
Step 1: Pair the numbers from right to left 5184 two pairs
Therefore answer is 2 digit numbers
72 = 49 and 82 = 64
49 is less than 51
Therefore first digit of square root is 7.
Look at last digit which is 4
As 22 = 4 and 82 = 64 both end with 4
Therefore the answer could be 72 or 78
As we know 752 = 5625 greater than 5184
Therefore √5184 is below 75
Therefore √5184 = 72
Example 2: √9216
Step 1: Pair the numbers from right to left 9216 two pairs
Therefore answer is 2 digit numbers
92 = 81 and 102 = 100
81 is less than 92
Therefore first digit of square root is 9.
Look at last digit which is 6
As 42 = 16 and 62 = 36 both end with 6
Therefore the answer could be 94 or 96
As we know 952 = 9025 less than 9216
Therefore √9216 is above 95
Therefore √9216 = 96
General method
Example 1: √2809
Step 1: Form the pairs from right to left which decide the number of digits in the square root. Here 2 pairs therefore 2 - digits in thesquare root
Step 2: Now √28, nearest squares is = 25
So first digit is 5 (from left)
Step 3: As 28 – 25 = 3 is reminder which forms 30 with the next digit 0.
Step 4: Multiply 2 with 5 to get 10 which is divisor 10 √2809
30
Now 3 × 10 = 30 30 = Q R
10 3 0
Step 5: As 32 = 9 and 9 – 9 (last digit of the number) = 0
∴ 2809 is a perfect square and √2809 = 53
Example 2: 3249
Step 1: Form the pairs form right to left which decided the number of digits in the square root. Here 2 pairs therefore 2 digits in the square root.
Step 2: Now 32 > 25 = 52 so the first digit in 5 (from left)
Step 3: 32 – 25 = 7 is remainder which form 74 with the next digit 4
5 7
Step 4: Multiply 2 with 5 to get 10 which is divisor 10√3249
Now 74 = Q R 7 4
107 4
Step 5: 72 = 49 and 49 – 49 = 0 (remainder is 4 which together with 9 form 49)
∴ 3249 is a perfect square and √3249 = 57
Example 3: √54 75 6
Step 1: Form the pairs from right to left therefore the square root of 54756 has 3-digits.
Step 2: 5 > 4 = 22 i.e. nearest square is 22 = 4
So first digit is 2 (from left)
Step 3: As 5 – 4 = 1 is remainder which form 14 with the next digit 4.
Step 4: Multiply 2 with 2 to get 4, which is divisor
2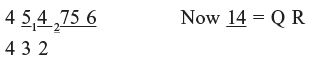
Step 5: Start with remainder and next digit, we get 27.
Find 27 – 32 = 27 – 9 = 18 [square of quotient]
234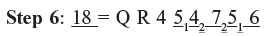
4 4 2
Now 25 – (3 × 4 × 2) = 25 – 24 = 1
1 = Q R
4 0 1
16 – 42 = 16 – 16 = 0
∴ 54756 is a perfect square and so √54756 = 234
|
38 videos|31 docs|9 tests
|
















