Digit sums, casting out 9’s and 9’ check method | Improve Your Calculations: Vedic Maths (English) - Class 6 PDF Download
| Table of contents |

|
| Introduction |

|
| Digit Sums |

|
| Cast Out Nine |

|
| Check Method |

|
Introduction
The word digit means a single figure number: The numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 are all digits. Big numbers can be reduced to single digit by adding the constituents.
Digit Sums
A digit sum is the sum of all the digits of a number and is found by adding all of the digits of a number
The digit sum of 35 is 3 + 5 = 8
The digit sum of 142 is 1 + 4 + 2 = 7
Note: If the sum of the digits is greater than 9, then sum the digits of the result again until the result is less than 10.
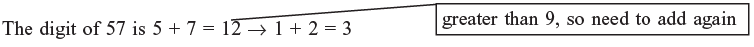 Hence the digit sum of 57 is 3.
Hence the digit sum of 57 is 3.
The digit sum of 687 is 6 + 8 + 7 = 21 → 2 + 4 = 3
Hence the digit sum of 687 is 3.
- Keep finding the digit sum of the result + until it's less than 10
- 0 and 9 are requivalent
Look and understand some more example:
To find the digit sum of 18, for the example we just add 1 and 8, i.e.1 + 8 =9 so the digit sum of 18 is 9. And the digit sum of 234 is 9 because 2 + 3+ 4 = 9
Following table shows how to get the digit sum of the following members:
15 6
12 3
42 6
17 8
21 3
45 9
300 3
1412 8
23 5
22 4
Sometimes two steps are needed to find a digit sum.
So for the digit sum of 29 we add 2 + 9 = 11 but since 11 is a 2-digit number we add again 1 + 1 = 1 So for the digit sum of 29 we can write 29 = 2 + 9 = 11 = 1 + 1 = 1
Similarity for 49 = 4 + 9 = 13 = 1 + 3 = 4
So the digit sum of 49 is 4.
Cast Out Nine
Adding 9 to a number does not affect its digit sum
So 5, 59, 95, 959 all have digit sum of 5.
For example, To find out the digit sum of 4939 we can cast out nines and just add up the 3 and 4 so digit sum is 7 or using the longer method we add all digit 4 + 9 + 3 + 9 = 25 = 2 + 5 = 7
There is another way of casting out the nines from number when you are finding its digit sum.
Casting out of 9’s and digit totalling 9 comes under the Sutra when the samuccaya is the same it is zero.
So in 465 as 4 and 5 total nine, they are cast out and the digit sum is 6: when the total is the same (as 9) it is zero (can be cast out) cancelling a common factor in a fraction is another example.
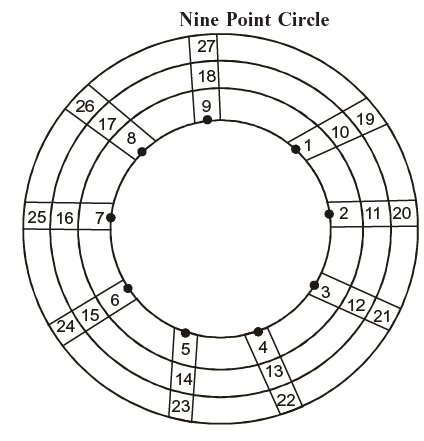
Number at each point on the circle have the same digit sum. By casting out 9's, finding a digit sum can be done more quickly and mentally.
Check Method
Digit sum can be used to check that the answers are correct.
Example: Find 23 + 21 and check the answer using the digit sums
23 = digit sum of 23 is 2 + 3 = 5
+ 21 = digit sum of 21 is 2 + 1 = 3
44 = digit sum of 44 is 4 + 4 = 8
If the sum has been done correctly, the digit sum of the answer should also be 8
Digit sum of 44 = 8 so according to this check the answer is probably correct.
There are four steps to use digit sum to check the answers:
1. Do the sum.
2. Write down the digit sums of the numbers being added.
3. Add the digit sums.
4. Check whether the two answers are same in digit sums.
Add 278 and 119 and check the answer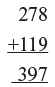 1. We get 397 for the answer
1. We get 397 for the answer
2. We find the digit sum of 278 and 119 which are, 8 and 2 respectively
3. Adding 8 and 2 gives 10, digits sum of 10 = 1 + 0 = 1
4. Digit sum of 397 is 3 + 9 + 7 = 19 = 1 + 9 = 10 = 1 + 0 = 1
Which confirm the answer?
Caution!
Check the following sum: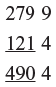
Here an estimation can help you to find the result more accurate if by mistage you write 400 in place of 490 then it will show the result is correct.
The check is 9 + 4 = 13 = 4 which is same as the digit sum of the answer which confirms the answer.
However, if we check the addition of the original number we will find that it is incorrect! This shows that the digit sum does not always find errors. It usually works but not always. We will be looking at another checking device i.e. 11 - check method.
Note: The difference of 9 and its multiples in the answer make errors. So, keep in mind a rough estimation.
|
36 videos|31 docs|3 tests
|
|
36 videos|31 docs|3 tests
|

|
Explore Courses for Class 6 exam
|

|
















