Fractions Made Easy | Mental Maths - Class 1 PDF Download
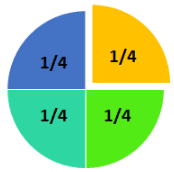
What is a fraction?
A fraction is a numerical quantity that is not a whole number.
For example,
1/4 is a fraction of
- 1 as numerator and
- 4 as a denominator
Types of Fractions
Like Fraction
Fractions having the same denominator are called like fractions.
For example,
- 1/2, 3/2, 5/2, and 7/2 are all like fractions.
Unlike Fractions
Fractions having different denominators are called, unlike fractions.
For example,
- 1/2, 2/3, 3/4 and 4/5 are all unlike fractions
Proper Fraction
A fraction whose numerator is less than the denominator is called proper fraction.
For example,
- 8/9, 7/8, 5/7 and 3/6 are all proper fractions.
Improper Fraction
A fraction whose numerator is greater than the denominator is called improper fraction.
For example,
- 3/2, 4/3, 8/4 and 7/5 are all improper fractions.
Equivalent Fraction
Fractions that represent the same or equal values are called equivalent fractions.
For example,
- 1/3, 2/6, 3/9 and 4/12 are all equivalent fractions, as all of them are equal to 1/3
Example 1: Find the fraction of the shaded and unshaded parts.
Sol:
Total Parts = 8
Fraction of shaded part = 3/8
Fraction of unshaded part = 5/8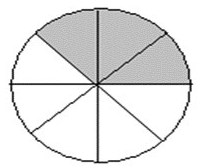
Example 2: Find the fraction of red balls, green balls and blue balls.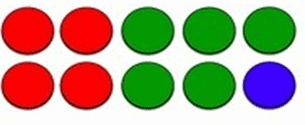
Sol:
Total number of balls= 10
Number of red balls= 4
Fraction of red balls= 4/10 = 2/5
Fraction of green balls = 5/10 = 1/2
Fraction of blue balls = 1/10
Fraction as a division
Any fraction can be expressed as a division by writing its numerator as dividend and denominator as divisor
Numerator/Denominator
- = Dividend ÷ Divisor
- =Dividend/Divisor
Example 1: Write 1÷2 as a fraction.
Sol: 1/2
Example 2: Write 2/3 as division.
Sol: 2÷3
To convert a mixed number into an improper fraction & vice versa
- To convert a mixed number into an improper fraction, multiply the quotient with the divisor and add the product with the remainder in the numerator. The denominator will contain the divisor.

- To convert an improper fraction into a mixed number, divide the numerator of the fraction by the denominator. Write the quotient as the whole number. The remainder in the numerator and the divisor is in the denominator.

Example 1: Fill in the blank 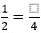
Sol: Checking our Denominators, we need to make 2 equivalent to 4
As 2 x 2 = 4
Therefore, 1 should be multiplied by 2, which gives 1 x 2 = 2
Hence, 2/4 is our answer.
Example 2: Check whether the fractions 2/3, and 3/4 are equal or not.
Sol: To check whether the fractions 2/3 and 3/4 are equal, we need to compare them and see if they represent the same value. Fractions are equal if their numerator and denominator ratios are the same. Let's perform the comparison:
Fraction 2/3:
Numerator = 2
Denominator = 3
Fraction 3/4:
Numerator = 3
Denominator = 4
To determine if they are equal, we can cross-multiply and check if the products are the same:
For 2/3:
2 * 4 = 8
For 3/4:
3 * 3 = 9
Since 8 is not equal to 9, we can conclude that the fractions 2/3 and 3/4 are not equal.
Finding and checking equivalent fraction
- To find the equivalent fraction to a given fraction, divide or multiply the numerator or denominator by the same number. (other than zero)

To find a fraction in its lowest term
- A fraction is in its lowest term when the numerator and the denominator don’t have a common factor, except 1.
- There are two methods of finding a fraction in its lowest term. They are:
Method 1:
Divide the numerator and denominator with their common factor till we are left with only the common factor, 1
Method 2:
Divide the numerator and denominator of the given fraction with their HCF.
Example 1: Find the lowest term of the fraction 12/24 using method 1.
Sol: 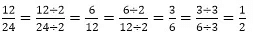
Example 2: Highest Common Factor (HCF) of 15 and 65 is 5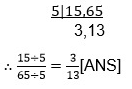
To find the fraction of a number or quantity
Divide the number by the denominator. Then, multiply the quotient so obtained by the numerator.
Example 1: A group has 120 children. 4/5 of them are girls. Find the number of boys.
Sol: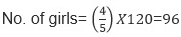
No. of boys= (120-96) = 24
Example 2: Find 1/4 of a year in months.
Sol: A year has 12 months.
1/4 X 12 = 3 months [ANS]
To compare unlike fractions
- First find the LCM of the denominators of the given fractions.
- Then convert the unlike fractions into equivalent like fractions with LCM as their common denominator.
- Compare the like fractions.
Convert mixed fractions into improper fractions to compare the
Example 1: Compare 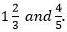
Sol: Convert all mixed fractions into improper fraction
Now we get 5/3 and 4/5
Take LCM of both the denominators (3 and 5)
The LCM of 3 and 5 is 15.
Now as 15/3 = 5, multiply 5/3 by 5
Similarly 15/5 = 3; multiply 4/5 by 3
Thus we need to compare 25/15 and 12/15
Since the denominator is same and 25 > 12, we have
25/15 > 12/15
Example 2: Arrange the following fractions in ascending and descending order.
1/2, 2/3, 3/4
Sol: LCM of 2, 3, 4 is 2 x 3 x 2 = 12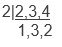
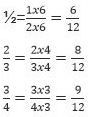
Denominator is common. And 9 > 8 > 6
Therefore, ascending order = 1/2 < 2/3 < 3/4
descending order = 3/4 > 2/3 > 1/2
To add/subtract unlike fractions
- Find the LCM of the denominators of unlike fractions.
- Then convert the unlike fraction into an equivalent like fraction with LCM as the common denominator.
- Add/subtract the like fraction so obtained.
Example 1: Add/subtract 1/2 and/from 1/6.
Sol:
Addition:
LCM of 2 and 6 is 2x3=6. 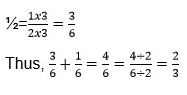
Subtraction: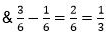
Multiplication of fractions
- Multiplication of a fraction by a whole number is the repeated addition of the fraction.
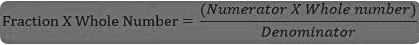
- To multiply two or more fractions, we multiply their numerators and their denominators. The ratio of the product of the numerator to the product of the denominator gives the new fraction.

Example 1: Find the value of 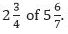
Sol: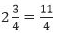
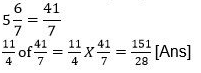
Example 2: A car goes 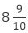 metres in one minute. How far will it go in
metres in one minute. How far will it go in 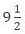 minutes?
minutes?
Sol: In one minute, the car goes 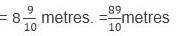
Distance traveled by the car in 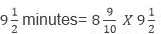
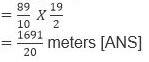
Reciprocal of a fractional number
When the product of two fractions is 1, we say that each of the fraction is the reciprocal or multiplicative inverse of the other.
Example 1: Find the reciprocal of 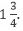
Sol: 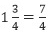
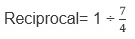
= 4/7
Division of fractions
- The division is repeated subtraction.
- Division by a fraction is the same as multiplication by its reciprocal.
0 has no reciprocal. - The reciprocal of 1 is 1.
- 0 divided by any non-zero number = 0
Example 1: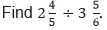
Sol: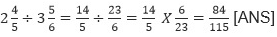
Example 2: A cloth is 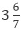 metre long. How many pieces of
metre long. How many pieces of 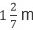 each can be cut from the rope?
each can be cut from the rope?
Sol: Number of pieces 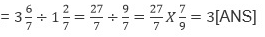
|
39 videos|158 docs|19 tests
|
FAQs on Fractions Made Easy - Mental Maths - Class 1
| 1. What is a fraction? |  |
| 2. How can mixed fractions be converted into improper fractions for comparison? |  |
| 3. How can fractions be multiplied together? |  |
| 4. What is the reciprocal of a fractional number? |  |
| 5. How can fractions be compared when the denominators are different? |  |

















