Multiplying Decimals | Mental Mathematics for Class 8 PDF Download

What are decimals?

All numbers are made up of digits: 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. Digits are like letters in a word. A word is made up of letters. Numbers are made up of digits: 23 is a two-digit number, made from the digits 2 and 3; 627 is a three-digit number made from the digits 6, 2 and 7. The position of the digit in the number tells us its value. For instance, the 2 in the number 23 has a value of 2 tens, and the 3 has a value of 3 ones. Numbers in the hundreds are three-digit numbers: 435, for example. The 4 is the hundreds digit and tells us there are 4 hundreds (400). Th  e tens digit is 3 and signifi es 3 tens (30). The units digit is 5 and signifi es 5 ones, or simply 5.

When we write a number, the position of each digit is important. The position of a digit gives that digit its place value. 

When we write prices, or numbers representing money, we use a decimal point to separate the dollars from the cents. For example, $2.50 represents 2 dollars and 50 hundredths of a dollar. The first digit after the decimal represents tenths of a dollar. (Ten 10¢ coins make a dollar.) The second digit after the decimal represents hundredths of a dollar. (One hundred cents make a dollar.) So $2.50, or two and a half dollars, is the same as 250¢. If we wanted to multiply $2.50 by 4, we could simply multiply the 250¢ by 4 to get 1,000¢. One thousand cents is the same as $10.00. 

Digits after a decimal point have place values as well. The number 3.14567 signifi es three ones, then after the decimal point we have one tenth, four hundredths, five thousandths, six ten-thousandths, and so on. So $2.75 equals two dollars, seven tenths of a dollar and five hundredths of a dollar. 

To multiply a decimal number by 10, we simply move the decimal point one place to the right. To multiply 1.2 by 10, we move the decimal one place to the right, giving an answer of 12. To multiply by 100, we move the decimal two places to the right. If there aren’t two digits, we supply them as needed by adding zeros. So, to multiply 1.2 by 100, we move the decimal two places, giving an answer of 120. 

To divide by 10, we move the decimal one place to the left. To divide by 100, we move the decimal two places to the left. To divide 14 by 100, we place the decimal after the 14 and move it two places to the left. The answer is 0.14. (We normally write a 0 before the decimal if there are no other digits.)
Now, let’s look at general multiplication of decimals.

Multiplication of Decimals

Multiplying decimal numbers is no more complicated than multiplying any other numbers. Let us take an example of 1.2 × 1.4.
We write down the problem as it is, but when we are working it out, we ignore the decimal points.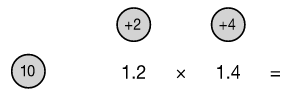
Although we write 1.2 × 1.4, we treat the problem as:
12 × 14 =
We ignore the decimal point in the calculation; we calculate 12 plus 4 is 16, times 10 is 160. Four times 2 is 8, plus 160 is 168.
The problem will look like this: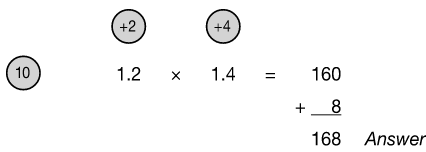
Our problem was 1.2 × 1.4, but we have calculated 12 × 14, so our work isn’t finished yet. We have to place a decimal point in the answer. To find where we put the decimal, we look at the problem and count the number of digits after the decimals in the multiplication. There are two digits after the decimals: the 2 in 1.2 and the 4 in 1.4. Because there are two digits after the decimals in the problem, there must be two digits after the decimal in the answer. We count two places from the right and put the decimal between the 1 and the 6, leaving two digits after it
1.68   Answer
An easy way to double-check this answer would be to approximate. That means, instead of using the numbers we were given, 1.2 × 1.4, we round off to 1.0 and 1.5. This gives us 1.0 times 1.5, which is 1.5, so we know the answer should be somewhere between 1 and 2. This tells us our decimal is in the right place. This is a good double-check. You should always make this check when you are multiplying or dividing using decimals. The check is simply: does the answer make sense?
Let’s try another.
9.6 × 97 =
We write the problem down as it is, but work it out as if the numbers are 96 and 97.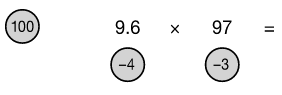
96 – 3 = 93    
93 × 100 (reference number) = 9,300    
4 × 3 = 12    
9,300 + 12 = 9,312

Where do we put the decimal? How many digits follow the decimal in the problem? One. That’s how many digits should follow the decimal in the answer.
931.2 Answer 

To place the decimal, we count the total number of digits following the decimals in both numbers we are multiplying. We will have the same number of digits following the decimal in the answer.
We can double-check the answer by estimating 10 times 90; from this we know the answer is going to be somewhere near 900, not 9,000 or 90. 

If the problem had been 9.6 × 9.7, then the answer would have been 93.12. Knowing this can enable us to take some shortcuts that might not be apparent otherwise. We will look at some of these possibilities shortly. In the meantime, try these problems. 

What if we had to multiply 0.13 × 0.14?
13 × 14 = 182
Where do we put the decimal? How many digits come after the decimal point in the problem? Four, the 1 and 3 in the first number and the 1 and 4 in the second. So we count back four digits in the answer. But wait a minute; there are only three digits in the answer. What do we do? We have to supply the fourth digit. So, we count back three digits, then supply a fourth digit by putting a 0 in front of the number. Then we put the decimal point before the 0, so that we have four digits after the decimal.
The answer looks like this:
.0182
We can also write another 0 before the decimal, because there should always be at least one digit before the decimal. Our answer would now look like this:
0.0182 

Let’s try some more:
0.014 × 1.4 =
14 × 14 = 196 

Where do we put the decimal? There are four digits after the decimal in the problem; 0, 1 and 4 in the first number and 4 in the second, so we must have four digits after the decimal in the answer. Because there are only three digits in our answer, we supply a 0 to make the fourth digit.
Our answer is 0.0196. 

Beating the system 

Understanding this simple principle can help us solve some problems that appear difficult using our method but can be adapted to make them easy.
Here is an example
8 × 79 =
What reference number would we use for this one? We could use 10 for the reference number for 8, but 79 is closer to 100. Maybe we could use 50. The speeds math method is easier to use when the numbers are close together. So, how do we solve the problem? Why not call the 8, 8.0? 

There is no difference between 8 and 8.0. The first number equals 8; the second number equals 8 too, but it is accurate to one decimal place. The value doesn’t change.
We can use 8.0 and work out the problem as if it were 80, as we did above. We can now use a reference number of 100. Let’s see what happens: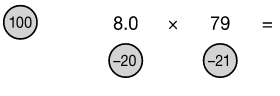

Now the problem is easy. Subtract diagonally.
79 – 20 = 59
Multiply 59 by the reference number (100) to get 5,900.
Multiply the numbers in the circles.
20 × 21 = 420
(To multiply by 20, we can multiply by 2 and then by 10.) Add the result to the subtotal.
5,900 + 420 = 6,320
The completed problem would look like this: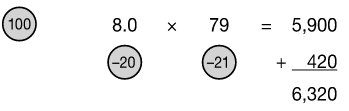

Now, we have to place the decimal. How many digits are there after the decimal in the problem? One, the 0 we provided. So we count one digit back in the answer.    
632.0  Answer

We would normally write the answer as 632.
Let’s check this answer using estimation. Eight is close to 10, so we can round upwards.
10 × 79 = 790
The answer should be less than, but close to, 790. It certainly won’t be around 7,900 or 79. Our answer of 632 fits, so we can assume it is correct.
We can double-check by casting out nines.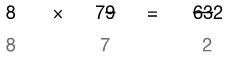

Eight times 7 equals 56, which reduces to 11, then 2. Our answer is correct.
Let’s try another.  
98 × 968 =

We write 98 as 98.0 and treat it as 980 during the calculation. Our problem now becomes 980 × 968.

Our next step is: 968 – 20 = 948
Multiply by the reference number:
948 × 1,000 = 948,000

Now multiply 32 by 20. To multiply by 20, we multiply by 2 and by 10.
32 × 2 = 64
64 × 10 = 640
It is easy to add 948,000 and 640.
948,000 + 640 = 948,640

We now have to adjust our answer because we were multiplying by 98, not 980.
Placing one digit after the decimal (or dividing our answer by 10), we get 94,864.0, which we simply write as 94,864.
Our full work would look like this: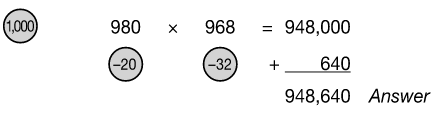

Let’s cast out nines to check the answer.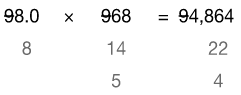

Five times 8 is 40, which reduces to 4. Our answer, 94,864, also reduces to 4, so our answer seems to be correct.
We have checked our answer, but casting out nines does not tell us if the decimal is in the correct position, so let’s double-check by estimating the answer.
Ninety-eight is almost 100, so we can see if we have placed the decimal point correctly by multiplying 968 by 100 to get 96,800. This has the same number of digits as our answer, so we can assume the answer is correct.