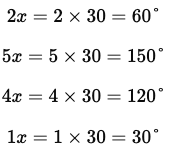Understanding Quadrilaterals Class 8 Worksheet Maths Chapter 3
| Table of contents |

|
| Multiple Choice Questions (MCQs) |

|
| True/False |

|
| Very Short Answer Questions |

|
| Short Answer Questions |

|
Multiple Choice Questions (MCQs)
Q1:How many sides does a regular polygon have if each of its interior angles is 165°?
A) 20
B) 22
C) 24
D) 26
Ans. C)
Sol:Total sum of all the exterior angles of a regular polygon = 360°
Let number of sides be n.
Measure of each interior angle = 165°
Measure of each exterior angle = 180° − 165° = 15° [Since an interior and an exterior angle forms a linear pair]
Number of sides = Sum of exterior angles / Each exterior angle
=360°/15 = 24
Q2: What will be the sum of interior angles of a polygon having 8 sides?
A) 720°
B) 1080°
C) 1260°
D) 1440°
Ans.B)
Sol: Sum of interior angles of polygon=(2n−4)⋅90
=(16−4)⋅90
=12 x 90
=1080°
Q3: Find out the number of sides of a regular polygon whose exterior angles are 60°.
A) 3
B) 4
C) 6
D) 12
Ans.C)
Sol: External Angle of a Regular Polygon = 360° / Total number of sides.
⇒ n × 60° = 360° gives n = 6.
Q4: The sides of a quadrilateral are in the ratio of 2:5:4:1. Find out the smallest angle.
A) 120°
B) 180°
C) 60°
D) 90°
Ans.C)
Sol: Let the first angle be = 2x
Let the second angle be = 5x
Let the third angle be = 4x
Let the fourth angle be = 1x (from the ratio given)
We know that the sum or addition of all the angles which are interior in the quadrilateral gives a total answer as 360°.
Therefore,
2x+5x+4x+1x = 360°
12x = 360°
x = 360/12
x= 30
The measure of all the interior angles of the quadrilateral
Q5: What is the name of a regular polygon of 3 sides?
A) Equilateral triangle
B) Square
C) Regular hexagon
D) Regular octagon
Ans. A)
Sol:A regular polygon of 3 sides is a triangle where all sides and angles are equal. This type of triangle is called an Equilateral Triangle.
True/False
Q1: A regular octagon has 1080 degree of total sum of interior angle.
Ans. True
Sol:Sum of interior angles = (n−2)×180°
Here, n=8.
Sum of interior angles = (8−2)×180°=6×180° = 1080°
Q2: A regular polygon with exterior angles of 80° has 7 sides.
Ans. False
Sol:
Therefore, regular polygon cannot have 7 sides if each exterior angle is 80°
Q3: A parallelogram has all the sides equal.
Ans. False
Sol: A parallelogram is a quadrilateral where opposite sides are parallel and equal in length. However, not all sides need to be equal. If all sides of a parallelogram are equal, it becomes a rhombus, which is a special type of parallelogram.
So, not all parallelograms have all sides equal.
Q4: Exterior angle sum of hexagon is 360°
Ans. True
Sol: The sum of the exterior angles of any polygon (regular or irregular) is always 360°, regardless of the number of sides.
Q5: The measure of exterior angle of regular polygon is 40°
Ans. True
Sol:
Very Short Answer Questions
Q1: Write down the formula of area of rhombus.
Ans. ½ × product of diagonals
Q2: Can all the angles of a quadrilateral be right angles?
Ans. Yes, all the angles of a quadrilateral can be right angles.
Q3: Name the quadrilateral whose diagonals are equal.
Ans.Square, rectangles
Q4: Each angle of a square measures ___°.
Ans.90°
Q5: How many parallel lines are in a trapezium?
Ans. 2
Q6: Which figure is equiangular and equilateral polygons?
Ans.Square, Triangle
Q7: A parallelogram can be rectangle if measure of each angle is _______.
Ans.90 degrees
Q8: If the diagonals of a quadrilateral are perpendicular bisectors of each other then it is always a______.
Ans. Rhombus
Q9: The sum of all angles in a quadrilateral is equal to_____ right angles.
Ans. 4
Short Answer Questions
Q1:ABCD is a parallelogram in which ∠A=110°. Find the measure of the angles B, C and D, respectively.
Ans. The measure of angle A=110°
The sum of all adjacent angles of a parallelogram is 180°
∠A + ∠B = 180
110°+ ∠B = 180°
∠B = 180°- 110°
= 70°.
Also ∠B + ∠C = 180° [Since ∠B and ∠C are adjacent angles]
70°+ ∠C = 180°
∠C = 180°- 70°
= 110°.
Now ∠C + ∠D = 180° [Since ∠C and ∠D are adjacent angles]
110o+ ∠D = 180°
∠D = 180°- 110°
= 70°
Q2:The two adjacent angles of a parallelogram are the same. Find the measure of each and every angle of the parallelogram.
Ans. A parallelogram with two equal adjacent angles.
To find:- the measure of each of the angles of the parallelogram.
The sum of all the adjacent angles of a parallelogram is supplementary.
∠A+∠B=180°
2∠A = 180°
∠A = 90°
∠B = ∠A = 90°
In a parallelogram, the opposite sides are the same.
Therefore,
∠C=∠A=90°
∠D=∠B=90°
Hence, each angle of the parallelogram measures 90°.
Q3: If three angles of a trapezium is 50°, 130° and 120°. Then find the other angle.
Ans.Given that the angles are 50 degrees, 130 degrees, and 120 degrees, you can find the fourth angle as follows:
Let the fourth angle be "x" degrees.
Given angles: 50°, 130°, 120°, x°
Since the sum of all angles of a quadrilateral is :
50°+130°+120° + x° = 180°
300 + x° = 180°
Now solving for "x":
x° = 360° - 300°
x° = 60°
So, the fourth angle in the trapezium is 60 degrees.
Q4: If two adjacent angles of a parallelogram are in the ratio 2:3 Find all the angles of the parallelogram.
Ans.Let P=2x and Q=3x
Since sum of all the angles of parallelogram is 360°
So, 2x + 3x =180°
5x=180°
x=180°/5
Therefore x=36°
So, P=2x
=> P=72°
and Q=3x
=> Q=108°
So R= 72° {angle opposite of P}
S=108° {angle opposite of Q}
Q5: If the angles of a quadrilateral are in the ratio 3:6:8:13. The largest angle is?
Ans.Let the angles are 3x,6x,8x,13x.
Since sum of all the angles of Quadrilateral is 360°
3x+6x+8x+13x=360°
30x=360°
x=12°
Thus, the largest angle is 156°.
Q6: The angles of a quadrilateral are x°, x+5°, x+10°, x+25°. Then find the value of x.
Ans.Since sum of all the angles of Quadrilateral is 360°
Therefore,
x+(x+5)+(x+10)+(x+25)=360°
x+x+5+x+10+x+25=360
4x+40=360°
4x=360°−40°
4x=320°
x=320°/4
x=80°
|
81 videos|423 docs|31 tests
|
FAQs on Understanding Quadrilaterals Class 8 Worksheet Maths Chapter 3
| 1. What are the properties of quadrilaterals? |  |
| 2. How do you classify different types of quadrilaterals? |  |
| 3. What is the difference between a square and a rectangle? |  |
| 4. How can the area of different quadrilaterals be calculated? |  |
| 5. What are the real-life applications of understanding quadrilaterals? |  |