Guesstimation | Mental Mathematics for Class 8 PDF Download

Introduction

So far you’ve been perfecting the mental techniques necessary to figure out the exact answers to math problems. Often, however, all you’ll want is a ballpark estimate. Say you’re getting quotes from different lenders on refinancing your home. All you really need at this information-gathering stage is a ballpark estimate of what your monthly payments will be. Or say you’re settling a restaurant bill with a group of friends and you don’t want to figure each person’s bill to the penny. The guesstimation methods described in this chapter will make both these tasks—and many more just like them—much easier. Addition, subtraction, division, and multiplication all lend themselves to guesstimation. As usual, you’ll do your computations from left to right.

Addition Guesstimation

Guesstimation is a good way to make your life easier when the numbers of a problem are too long to remember. The trick is to round the original numbers up or down: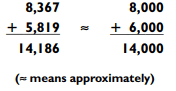

Notice that we rounded the first number down to the nearest thousand and the second number up. Since the exact answer is 14,186, our relative error is small.
If you want to be more exact, instead of rounding off to the nearest thousand, round off to the nearest hundred:

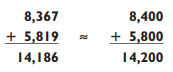
The answer is only 14 off from the exact answer, an error of less than .1%. This is what I call a good guesstimation!
Try a five-digit addition problem, rounding to the nearest hundred: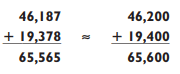
By rounding to the nearest hundred, our answer will always be off by less than 100. If the answer is larger than 10,000, your guesstimate will be within 1% of the exact answer.
Now let’s try something wild: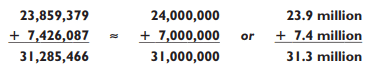

If you round to the nearest million, you get an answer of 31 million, off by roughly 285,000. Not bad, but you can do better by rounding to the nearest hundred thousand, as we’ve shown in the right-hand column. Again your guesstimate will be within 1% of the precise answer. If you can compute these smaller problems exactly, you can guesstimate the answer to any addition problem.

Guesstimating at the Supermarket 

Let’s try a real-world example. Have you ever gone to the store and wondered what the total is going to be before the cashier rings it up? For estimating the total, my technique is to round the prices to the nearest 50¢. For example, while the cashier is adding the numbers shown below on the left, I mentally add the numbers shown on the right: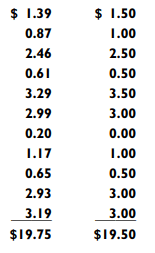
My final figure is usually within a dollar of the exact total.

Subtraction Guesstimation 

The way to guesstimate the answers to subtraction problems is the same—you round to the nearest thousand or hundreds digit, preferably the latter: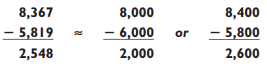

You can see that rounding to the nearest thousand leaves you with an answer quite a bit off the mark. By rounding to the second digit (hundreds, in the example), your answer will usually be within 3% of the exact answer. For this problem, your answer is off by only 52, a relative error of 2%. If you round to the third digit, the relative error will usually be below 1%. For instance: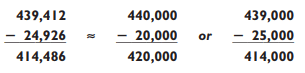

By rounding the numbers to the third digit rather than to the second digit, you improve the accuracy of the estimate by a significant amount.

Division Guesstimation

The first, and most important, step in guesstimating the answer to a division problem is to determine the magnitude of the answer: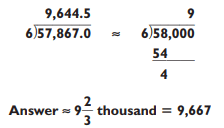

The next step is to round off the larger numbers to the nearest thousand and change the 57,867 to 58,000. Dividing 6 into 58 gives you 9 with a remainder. But the most important component in this problem is where to place the 9.

For example, multiplying 6 x 90 yields 540, while multiplying 6 x 900 yields 5,400, both of which are too small. But 6 x 9,000 = 54,000, which is pretty close to the answer. This tells you the answer is 9,000 and something. You can estimate just what that something is by first subtracting 58 - 54 = 4. At this point you could bring down the 0 and divide 6 into 40, and so forth. But if you’re on your toes, you’ll realize that dividing 6 into 4 gives you 4/6 = 2/3 ≈ . 667.  Since you know the answer is 9,000 something, you’re now in a position to guess 9,667. In fact, the actual answer is 9,645—darn close! 

Division on this level is simple. But what about large division problems? Let’s say we want to compute, just for fun, the amount of money a professional athlete earns a day if he makes $5,000,000 a year: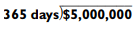

First you must determine the magnitude of the answer. Does this player earn thousands every day? Well, 365 x 1000 = 365,000, which is too low.
Does he earn tens of thousands every day? Well, 365 x 10,000 = 3,650,000, and that’s more like it. To guesstimate your answer, divide the first two digits (or 36 into 50) and figure that’s 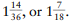 Since 18 goes into 70 about 4 times, your guess is that the athlete earns about $14,000. The exact answer is $13,698.63 per day. Not a bad estimate (and not a bad salary!).
Here’s an astronomical calculation for you. How many sec onds does it take light to get from the sun to the earth? Well, light travels at 186,282 miles per second, and the sun is (on average) 92,960,130 miles away. I doubt you’re particularly eager to attempt this problem by hand. Fortunately, it’s relatively simple to guesstimate an answer. First, simplify the problem:

Now divide 186 into 930, which yields 5 with no remainder. Then append the two 0s you removed from 93,000 and you get 500 seconds. The exact answer is 499.02 seconds, so this is a very respectable guesstimate.

Multiplication Guesstimation

You can use much the same techniques to guesstimate your answers to multiplication problems. For example,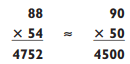
Rounding up to the nearest multiple of 10 simplifies the problem considerably, but you’re still off by 252, or about 5%. You can do better if you round both numbers by the same amount, but in opposite directions. That is, if you round 88 by increasing 2, you should also decrease 54 by 2: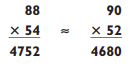

Instead of a 1-by-1 multiplication problem, you now have a 2-by-1 problem, which should be easy enough for you to do. Your guesstimation is off by only 1.5%. 

When you guesstimate the answer to multiplication problems by rounding the larger number up and the smaller number down, your guesstimate will be a little low. If you round the larger number down and the smaller number up so that the numbers are closer together, your guesstimate will be a little high. The larger the amount by which you round up or down, the greater your guesstimate will be off from the exact answer. For example: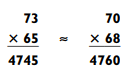
Since the numbers are closer together after you round them off, your guesstimate is a little high.
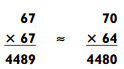Since the numbers are farther apart, the estimated answer is too low, though again, not by much. You can see that this multiplication guesstimation method works quite well. Also notice that this problem is just 67² and that our approximation is just the first step of the squaring techniques. Let’s look at one more example:
We observe that the approximation is most accurate when the original numbers are close together. Try estimating a 3-by-2 multiplication problem:

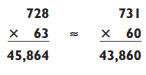
By rounding 63 down to 60 and 728 up to 731, you create a 3-by-1 multiplication problem, which puts your guesstimate within 2004 of the exact answer, an error of 4.3%. Now try guesstimating the following 3-by-3 problem: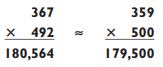

You will notice that although you rounded both numbers up and down by 8, your guesstimate is off by over 1000. That’s because the multiplication problem is larger and the size of the rounding number is larger, so the resulting estimate will be off by a greater amount. But the relative error is still under 1%.

How high can you go with this system of guesstimating multiplication problems? As high as you want. You just need to know the names of large numbers. A thousand thousand is a million, and a thousand million is a billion. Knowing these names and numbers, try this one on for size: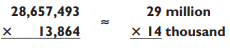

As before, the objective is to round the numbers to simpler numbers such as 29,000,000 and 14,000. Dropping the 0s for now, this is just a 2-by-2 multiplication problem: 29 x 14 = 406 (29 x 14  29 x 7 x 2  203 x 2 = 406). Hence the answer is roughly 406 billion, since a thousand million is a billion.

Square Root Estimation

Divide and Average

The quantity √n, the square root of a number n, is the number which, when multiplied by itself, will give you n. For example, the square root of 9 is 3 because 3 x 3 = 9. The square root is used in many science and engineering problems and is almost always solved with a calculator. The following method provides an accurate estimate of the answer. 

In square root estimation your goal is to come up with a number that when multiplied by itself approximates the original number. Since the square root of most numbers is not a whole number, your estimate is likely to contain a fraction or decimal point. 

Let’s start by guesstimating the square root of 19. Your first step is to think of the number that when multiplied by itself comes closest to 19. Well, 4 x 4 = 16 and 5 x 5 = 25. Since 25 is too high, the answer must be 4 point something. Your next step is to divide 4 into 19, giving you 4.75. Now, since 4 x 4 is less than 4 x 4.75 = 19, which in turn is less than 4.75 x 4.75, we know that 19 (or 4 x 4.75) lies between 4² and 4.75². Hence, the square root of 19 lies between 4 and 4.75.
I’d guess the square root of 19 to be about halfway between, at 4.375. In fact, the square root of 19 (rounded to three decimal places) is 4.359, so our guesstimate is pretty close. We illustrate this procedure as follows:

Actually, we can obtain this answer another way, which you might find easier. We know 4 squared is 16, which is shy of 19 by 3. To improve our guess, we “add the error divided by twice our guess.” Here, we add 3 divided by 8 to get  We note that this method will always produce an answer that is a little higher than the exact answer.
Now you try a slightly harder one. What’s the square root of 87?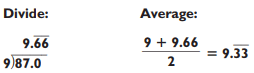

First come up with your ballpark figure, which you can get fairly quickly by noting that 9 x 9 = 81 and 10 x 10 = 100, which means the answer is 9 point something. Carrying out the division of 9 into 87 to two decimal places, you get 9.66. To improve your guesstimate, take the average of 9 and 9.66, which is 9.33—exactly the square root of 87 rounded to the second decimal place! Alternatively, our guesstimate is 9 + (error)/18

Using this technique, it’s pretty easy to guesstimate the square root of two-digit numbers. But what about three-digit numbers? Actually, they are not much harder. I can tell you right off the bat that all three-digit and four-digit numbers have two-digit square roots before the decimal point. And the procedure for computing square roots is the same, no matter how large the number. For instance, to compute the square root of 679, first find your ballpark figure. Because 20 squared is 400 and 30 squared is 900, the square root of 679 must lie between 20 and 30.

When you divide 20 into 679, you get approximately 34. Averaging 20 and 34 gives you a guesstimate of 27, but here’s a better estimate. If you know that 25 squared is 625, then your error is 679 - 625 = 54. Dividing that by 50, we have 54/50 = 108/100 = 1.08. Hence our improved guesstimate is 25 + 1.08 = 26.08. (For an even better estimate, if you know that 26 squared is 676, your error is 3, so add 3/52 ≈ .06 to get 26.06.) The exact answer is 26.06, rounded to two decimal places. To guesstimate the square root of four-digit numbers, look at the first two digits of the number to determine the first digit of the square root. For example, to find the square root of 7369, consider the square root of 73. Since 8 x 8 = 64 and 9 = 9 = 81, 8 must be the first digit of the square root. So the answer is 80 something. Now proceed the usual way. Dividing 80 into 7369 gives 92 plus a fraction, so a good guesstimate is 86. If you squared 86 to get 7396, you would be high by 27, so you should subtract 27/172 ≈ .16  for a better guesstimate of 85.84, which is right on the money.

To guesstimate the square root of a six-digit number like 593,472 would seem like an impossible task for the uninitiated, but for you it’s no sweat. Since 700² =  490,000, and 800² = 640,000, the square of 593,472 must lie between 700 and 800. In fact, all five-digit and six-digit numbers have three-digit square roots. In practice, you only need to look at the square root of the first two digits of six-digit numbers (or the first digit of five numbers). Once you figure out that the square root of 59 lies between 7 and 8, you know your answer is in the 700s. Now proceed in the usual manner: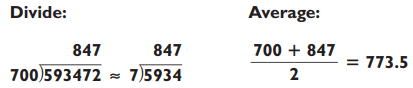

The exact square root of 593,472 is 770.37 (to five places), so you’re pretty close. But you could have been closer, as the following trick demonstrates. Note that the first two digits, 59, are closer to 64 (8 x 8) than they are to 49 (7 x 7). Because of this you can start your guesstimation with the number 8 and proceed from there: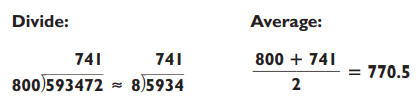

Just for fun, let’s do a real whopper—the square root of 28,674,529. This isn’t as hard as it might seem. Your first step is to round to the nearest large number—in this case, just find the square root of 29.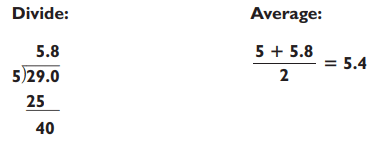

All seven-digit and eight-digit numbers have four-digit square roots, so 5.4 becomes 5400, your estimate. The exact answer is slightly greater than 5354.8. Not bad!
This wraps up the chapter on guesstimation math. After doing the exercises below, turn to the next chapter on pencil-and-paper math, where you will learn to write down answers to problems, but in a much quicker way than you’ve done on paper before.

More Tips on Tips 

As we indicated in Chapter 0, it is easy to figure out tips for most situations. For example, to figure out a 10% tip, we merely multiply the bill by 0.1 (or divide the bill by 10). For example, if a bill came to $42, then a 10% tip would be $4.20. To determine a 20% tip, you simply multiply the bill by 0.2, or double the amount of a 10% tip. Thus a 20% tip on a $42 bill would be $8.40. 

To determine a 15% tip, we have a few options. If you have mastered the techniques of Chapter 2, and are comfortable with multiplying by 15 = 5 x 3, you can simply multiply the bill by 15, then divide by 100. For example, with a $42 bill, we have 42 x 15 = 42 x 5 x 3 = 210 x 3 = 630, which when divided by 100, gives us a tip of $6.30. Another method is to take the average of a 10% tip and a 20% tip. From our earlier calculation, this would be

Perhaps the most popular approach to taking a 15% tip is to take 10% of the bill, cut that amount in half (which would be a 5% tip), then add those two numbers together. So, for instance, with a $42 bill, you would add $4.20 plus half that amount, $2.10, to get

$4.20 + $2.10  = $6.30

Let’s use all three methods to compute 15% on a bill that is $67. By the direct method, 67 x 3 x 5 = 201 x 5 = 1005, which when divided by 100 gives us $10.05. By the averaging  method, we average the 10% tip of $6.70 with the 20% tip of $13.40, to get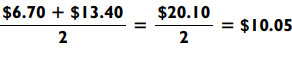

Using the last method, we add $6.70 to half that amount, $3.35 to get

$6.70 +  $3.35  = $10.05

Finally, to calculate a 25% tip, we offer two methods. Either multiply the amount by 25, then divide by 100, or divide the amount by 4 (perhaps by cutting the amount in half twice). For example, with a $42 bill, you can compute 42 x 25 =  42 x 5 x 5  = 210 x 5 = 1050, which when divided by 100 produces a tip of $10.50. Or you can divide the original amount directly by 4, or cut in half twice: half of $42 is $21, and half of that is $10.50. With a $67 bill, I would probably divide by 4 directly: since 67 = 4 = 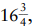 we get a 25% tip of $16.75.

Not-Too-Taxing Calculations

In this section, I will show you my method for mentally estimating sales tax. For some tax rates, like 5% or 6% or 10%, the calculation is straightforward. For example, to calculate 6% tax, just multiply by 6, then divide by 100. For instance, if the sale came to $58, then 58 x 6 = 348, which when divided by 100 gives the exact sales tax of $3.48. (So your total amount would be $61.48.)
But how would you calculate a sales tax of 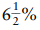  on $58?

I will show you several ways to do this calculation, and you choose the one that seems easiest for you. Perhaps the easiest way to add half of a percent to any dollar amount is to simply cut the dollar amount in half, then turn it into cents. For example, with $58, since half of 58 is 29, simply add 29 cents to the 6% tax (already computed as $3.48) to get a sales tax of $3.77. Another way to calculate the answer (or a good mental estimate) is to take the 6% tax, divide it by 12, then add those two numbers. For example, since 6% of $58 is $3.48, and 12 goes into 348 almost 30 times, then add 30 cents for an estimate of $3.78, which is only off by a penny. If you would rather divide by 10 instead of 12, go ahead and do it. You will be calculating 6.6% instead of 6.5% (since 6/10 = 0.6) but that should still be a very good estimate. Here, you would take $3.48 and add 34¢ to get $3.82. 

Let’s try some other sales tax percentages. How can we calculate 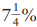 sales tax on $124? Begin by computing 7% of 124. From the methods shown in Chapter 2, you know that 124 x 7 = 868, so 7% of 124 is $8.68. To add a quarter percent, you can divide the original dollar amount by 4 (or cut it in half, twice) and turn the dollars into cents. Here, 124  = 4 = 31, so add 31¢ to $8.68 to get an exact sales tax of $8.99.

Another way to arrive at 31¢ is to take your 7% sales tax, $8.68, and divide it by 28. The reason this works is because 7/28 = 1/4. For a quick mental estimate, I would probably divide $8.68 by 30, to get about 29¢, for an approximate total sales tax of $8.97. 

When you divide by 30, then you are actually computing a tax of 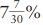, which is approximately 7.23% instead of 7.25%. How would you calculate a sales tax of 7.75%? Probably for most approximations, it is sufficient to just say that it is a little less than 8% sales tax. But to get a better approximation, here are some suggestions. As you saw in the last example, if you can easily calculate a 1/4% adjustment, then simply triple that amount for the 3/4% adjustment. For example, to calculate 7.75% of $124, you first calculate 7% to obtain $8.68. If you calculated that 1/4% is 31¢, then 3/4% would be 93¢, for a grand total of $8.68 + 0.93 = $9.61. For a quick approximation, you can exploit the fact that 7/9 =  .777 is approximately .75, so you can divide the 7% sales tax by 9 to get slightly more than the .75% adjustment. In this example, since $8.68 divided by 9 is about 96¢, simply add $8.68 + 0.96 = $9.64 for a slight overestimate. 

We can use this approximation procedure for any sales tax. For a general formula, to estimate the sales tax of $A.B%, first multiply the amount of the sale by A%. Then divide this amount by the number D, where A/D is equal to 0.B. (Thus D is equal to A times the reciprocal of B.) Adding these numbers together gives you the total sales tax (or an approximate one, if you rounded D to an easier nearby number). For instance, with 7.75%, the magic divisor D would be 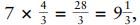, which we rounded down to 9. For sales tax of 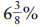, first compute the sales tax on 6%, then divide that number by 16, since 6/16 = 3/8. (To divide a number by 16, divide the number by 4 twice, or divide the number by 8, then by 2.) Try to come up with methods for finding the sales tax in the state that you live in. You will find that the problem is not as taxing as it seems! 

Some “INTEREST-ING” Calculations

Finally, we’ll briefly mention some practical problems pertaining to interest, from the standpoint of watching your investments grow, and paying off money that you owe.
We begin with the famous Rule of 70, which tells you approximately how long it takes your money to double: To find thenumber of years that it will take for your money to double, divide the number 70 by the rate of interest. Suppose that you find an investment that promises to pay you 5% interest per year. Since 70/ 5 = 14, then it will take about 14 years for your money to double. For example, if you invested $1000 in a savings account that paid that interest, then after 14 years, it will have $1000(1.05)¹⁴  $1979.93. With an interest rate of 7%, the Rule of 70 indicates that it will take about 10 years for your money to double. Indeed, if you invest $1000 at that annual interest rate, you will have after ten years $1000(1.07)¹⁰  = $1967.15. At a rate of 2%, the Rule of 70 says that it should take about 35 years to double, as shown below:

$1000(1.02)³⁵  = $1999.88 

A similar method is called the Rule of 110, which indicates how long it takes for your money to triple. For example, at 5% interest, since 110/5 =22, it should take about 22 years to turn $1000 into $3000. This is verified by the calculation $1000(1.05)²² = $2925.26. The Rule of 70 and the Rule of 110 are based on properties of the number e = 2.71828 . . . and “natural logarithms” (studied in precalculus), but fortunately we do not need to utilize this higher mathematics to apply the rules.
Now suppose that you borrow money, and you have to pay the money back. For example, suppose that you borrow $360,000 at an annual interest rate of 6% per year (which we shall interpret to mean that interest will accumulate at a rate of 0.5% per month) and suppose that you have thirty years to pay off the loan. About how much will you need to pay each month? First of all, you will need to pay $360,000 times 0.5% = $1,800 each month just to cover what you owe in interest. (Although, actually, what you owe in interest will go down gradually over time.)

Since you will make 30 x 12 = 360 monthly payments, then paying an extra $1,000 each month would cover the rest of the loan, so an upper bound on your monthly payment is $1,800 + $1,000 = $2,800. But fortunately you do not need to pay that much extra. Here is my rule of thumb for estimating your monthly payment.
Let i be your monthly interest rate. (This is your annual interest rate divided by 12.) Then to pay back a loan of $P in N months, your monthly payment M is about

In our last example, P = $360,000, and i = 0.005, so our formula indicates that our monthly payment should be about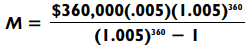

Notice that the first two numbers in the numerator multiply to $1,800. Using a calculator (for a change) to compute (1.005)³⁶⁰ = 6.02, we have that your monthly payment should be about $1,800(6.02)/5.02, which is about $2,160 per month.
Here’s one more example. Suppose you wish to pay for a car, and after your down payment, you owe $18,000 to be paid off in five years, with an annual interest rate of 4%. If there was no interest, you would have to pay $18,000/60 = $300 per month. Since the first year’s interest is $18,000(.04) = $720, you know that you will need to pay no more than $300 + $60 = $360. Using our formula, since the monthly interest rate is i  = 04/12 = 0.00333, we have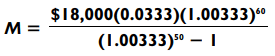

and since (1.00333)⁶⁰ = 1.22, we have a monthly payment of about $60(1.22)/(0.22)  $333.
We conclude with some exercises that we hope will hold your interest.