Class 8 Maths - Direct and Inverse Proportions CBSE Worksheets
Q1: The cost of 7m of a particular quality of pipe is ₹200 tabulate the cost of 4 meter of pipe of the same type.
(a) 114.28
(b) 28.114
(c) 11.42
(d) 1.428
Ans: (a)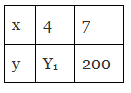 Therefore x1/y1 = x2/y2
Therefore x1/y1 = x2/y2
4/y1 = 7/200
= 4×200/7 = y1
y1 = 800/7 = 114.28
Q2: A train is moving at a uniform speed of 60 km/hr. How far will it travel in 30 minutes?
(a) 20
(b) 25
(c) 30
(d) 40
Ans: (c)
Given that the travelled 60 km per hour i.e., 60 km in 60 minutes,
so, 60/60 = x/30
x = 30 minutes
So the train will cover a distance 30 km in 30 minutes.
Q3: The scale of map is given as 1:40000000 two cities are 3cm apart on the map. Find the actual distance between them?
(a) 1400
(b) 1300
(c) 1200
(d) 1100
Ans: (c)
Let the map distance be x cm and actual distance by y cm then,
1:40000000 = x:y, where x = 4
1/4×107 = x/y
1/4×107 = 4/y
y = 4×3×107 = 12×107 cm = 1200 km
Q4: A train is moving at uniform speed of 60km/hr. Find the time required to cover a distance 200 km?
(a) 200 min
(b) 300 min
(c) 60 min
(d) 250 min
Ans: (a)
Given that train travels 60 km per hour i.e., 60 km in 60 minutes,
so, 60/60 = 200/y
y = 200 minutes
Q5: A machine in Cocacola factory fills 640 bottles in 4 hours. How many bottles will it fill in 5 hours?
(a) 700
(b) 1000
(c) 900
(d) 800
Ans: (d)
Given that, the factory fills 640 bottles in 4 hours,
so, 640/4 = x/5
160×5 = x
x = 800
Q6: 5 pipes are required to fill a tank in 1 hour 20 minute. How long will it take if only 4 pipes of the same type are used?
(a) 200 min
(b) 100 min
(c) 60 min
(d) 40 min
Ans: (b)
5 pipes filled the tank in 1 hr 20 minutes i.e., 80 minutes
Let the desired time to fill the tank x minutes.
Lesser the number of pipes, more will be the time required by it to fill the tank,
So, this is a case of inverse proportion 80×5 = x×4
x =80×5/4
x = 100 minutes
Q7: If 10 workers can build a wall in 40 hours how many workers will be required to do the same work in 20 hours?
(a) 10
(b) 30
(c) 20
(d) 40
Ans: (c)
Given that 10 workers can build a wall in 40 hours
Let y workers can build the wall in 20 hours
so, 40×10 = 20×y
40×10 = y
y = 20
Q8: Observe the following tables and find which pair of variables are in inverse proportion.
(a)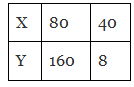 (b)
(b)
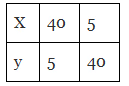 (c)
(c)
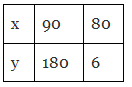 (d)
(d)
 Ans: (d)
Ans: (d)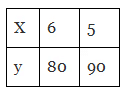 This table is in the inverse tables.
This table is in the inverse tables.
Q9: There are 50 students in hostel. Food provision for them is for 20 days. How long will these provision last 50 more students join the group?
(a) 15
(b) 20
(c) 30
(d) 10
Ans: (d)
New number of students = 50+50=100
so, 50×20 = 100×y
50×20/100 = y
y = 10
Q10: A batch of mango were packed in 25 boxes with 20 mangoes in each box if the same batch is packed using 25 mangoes in each box, how many boxes would be filed?
(a) 10
(b) 30
(c) 40
(d) 20
Ans: (d)
25×20 = y× 25
25×20/25 = y
y = 20
20 boxes would be filled
Q11: A farmer has enough food to feed 30 animals in his cattle for 6 days. How long would the food last if there were 12 animals in his cattle?
(a) 14
(b) 12
(c) 15
(d) 13
Ans: (c)
30×6 = 12×y
30×6/12 = y
y = 15
Q12: Motorcycles takes 2 hour to reach a destination by travelling at the speed of 40km/hr. How long will it take when the motor travels at the speed of 80 km/hr?
(a) 1hr
(b) 2hr
(c) 1.30hr
(d) 2.30hr
Ans: (a)
2×40 = 80×y
2×40/80 = y
y = 80/80
y = 1hr
Q13: A loaded train travels 28km in 30 minutes. If the speed remains the same, how far can it travel in 5 hours?
(a) 100
(b) 210
(c) 240
(d) 280
Ans: (d)
Given that the train can travel 28 km in 30 min
30 min = 1/2 hr
28/(1/2) = x/5
28×2×5 = x
x = 280 km
Q14: The cost of 10 meters of particular quality of cloth ₹200 tabulate the cost of 8 meters of cloth the same type.
(a) 120
(b) 140
(c) 160
(d) 180
Ans: (c)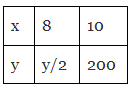 x1/y1 = x2/y2,
x1/y1 = x2/y2,
10/200 = 8/y2,
20 × 8 = y2
y2 = Rs 160
Q15: An electric pole 18 meters high castle shadow of 10 meters. Find the height of electric pole that cost a shadow of 20 meters under similar condition?
(a) 32
(b) 36
(c) 34
(d) 40
Ans: (b)
18/10 = x/20
18×20/10 = x
x= 36
|
79 videos|409 docs|31 tests
|
FAQs on Class 8 Maths - Direct and Inverse Proportions CBSE Worksheets
| 1. What is the difference between direct and inverse proportions? |  |
| 2. How can I identify if two variables are directly or inversely proportional? |  |
| 3. Can you provide a real-life example of direct proportionality? |  |
| 4. What are some practical applications of inverse proportions? |  |
| 5. How do you solve problems involving direct and inverse proportions? |  |


















