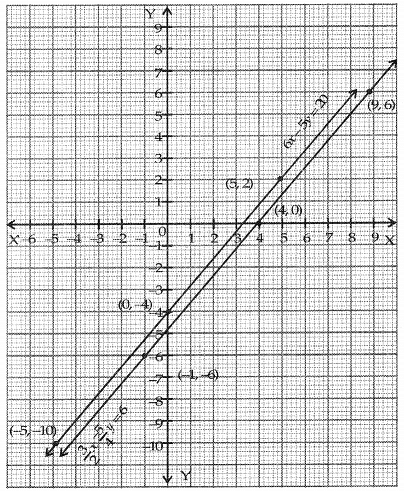
Pair of Linear Equations in Two Variables Class 10 Worksheet Maths Chapter 3
| Table of contents |

|
| Multiple Choice Questions |

|
| Fill in the blanks |

|
| Very Short Answer Questions |

|
| Short Answer Type Questions |

|
| Long Answer Type Questions |

|
Multiple Choice Questions
Q1: A pair of linear equations which have a unique solution x = 2, y = – 3 is:
(a) 2x – 3y = – 5, x + y = – 1
(b) 2x + 5y + 11 = 0, 4x + 10y + 22 = 0
(c) x – 4y – 14 = 0, 5x – y – 13 = 0
(d) 2x – y = 1, 3x + 2y = 0
Ans:(b) x – 4y – 14 = 0, 5x – y – 13 = 0
Sol:
1. 2x + 5y + 11 = 0
2. 4x + 10y + 22 = 0
Substituting x = 2 and y = -3
Equation 1: 2(2) + 5(-3) + 11 = 4 - 15 + 11 = 0 (satisfied)
Equation 2: 4(2) + 10(-3) + 22 = 8 - 30 + 22 = 0 (satisfied)
Q2: If a system of a pair of linear equations in two unknowns is consistent, then the lines representing the system will be
(a) parallel
(b) always coincident
(c) always intersecting
(d) intersecting or coincident
Ans: (d) intersecting or coincident
Sol: A consistent system of linear equations means that there is at least one solution. This can occur in two scenarios:
- Intersecting Lines: The lines intersect at exactly one point, meaning there is one unique solution.
- Coincident Lines: The lines lie on top of each other, meaning there are infinitely many solutions.
Q3: The pair of equations x = 0 and y = 0 has
(a) one solution
(b) two solutions
(c) infinitely many solutions
(d) no solution
Ans: (a) one solution
Sol: The equations x=0 and y=0 represent the x-axis and y-axis respectively.
The only point where these two lines intersect is at the origin, which is the point (0,0). Therefore, there is exactly one solution to this system of equations
Q4: A pair of system of equations x = 2, y = -2; x = 3, y = – 3 when represented graphically enclose
(a) Square
(b) Trapezium
(c) Rectangle
(d) Triangle
Ans: (c) Rectangle
Sol: The equations x=2 andx=3 represent vertical lines, while y=−2 and y=−3 represent horizontal lines. The intersection points of these lines are (2,−2), (2,−3), (3,−2), and (3,−3). These points form the vertices of a rectangle, making the shape enclosed by these lines a rectangle on the graph.
Q5: If two lines are parallel to each other then the system of equations is
(a) consistent
(b) inconsistent
(c) consistent dependent
(d) (a) and (c) both
Ans: inconsistent
Sol: If two lines are parallel, they never intersect, meaning there is no solution to the system of equations. Thus, the system is inconsistent.
Fill in the blanks
Q1: If in a system of equations corresponding to coefficients of member, equations are proportional then the system has ______________ solution (s).
Ans: infinite
Q2: A pair of linear equations is said to be inconsistent if its graph lines are ____________.
Ans: parallel
Q3: A pair of linear equations is said to be ____________ if its graph lines intersect or coincide.
Ans: Consistent
Q4: A consistent system of equations where straight lines fall on each other is also called _____________ system of equations.
Ans: Dependent
Q5: Solution of linear equations representing 2x – y = 0, 8x + y = 25 is ____________ .
Ans: x = 2.5, y = 5
Sol:
1. From 2x - y = 0, we can express y as:
y = 2x
2. Substitute y into the second equation 8x + y = 25:
8x + 2x = 25
10x = 25 → x = 25/10 = 2.5
3. Substitute x = 2.5 back into y = 2x:
y = 2(2.5) = 5
Thus, the solution is x = 2.5 and y = 5,
Very Short Answer Questions
Q1: In Fig., ABCD is a rectangle. Find the values of x and y.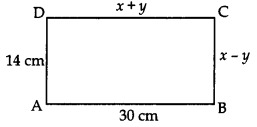
Sol: Since ABCD is a rectangle
⇒ AB = CD and BC = AD
x + y = 30 …………….. (i)
x – y = 14 ……………. (ii)
(i) + (ii) ⇒ 2x = 44
⇒ x = 22
Plug in x = 22 in (i)
⇒ 22 + y = 30
⇒ y = 8
Q2: Graphically, determine whether the following pair of equations has no solution, a unique solution, or infinitely many solutions:
(1) 2x - 3y + 4 = 0
(2) 4x - 6y + 8 = 0
Sol: Identify the System of Equations:
(1) 2x - 3y + 4 = 0
(2) 4x - 6y + 8 = 0Compare the Equations by Scaling:
Notice that Equation (2) is simply Equation (1) multiplied by 2.
2 × (2x - 3y + 4) = 4x - 6y + 8
This simplifies to:
4x - 6y + 8 = 0, which is identical to Equation (2).
Therefore, these two lines are coincident. Therefore, they represent the same line.
Conclusion:
The system of equations has infinitely many solutions because both equations represent the same line.
Q3: If 51x + 23y = 116 and 23x + 51y = 106, then find the value of (x – y).
Sol: Given equations are:
51x + 23y = 116 ……….. (i)
23x + 51y = 106 ………… (ii)
Subtracting (ii) from (i)
28x – 28y = 10
28(x – y) = 10
⇒ (x – y) ==
514
Q4: For what value of V does the point (3, a) lie on the line represented by 2x – 3y = 5?
Sol: Since (3, a) lies on the equation 2x – 3y = 5.
∴ (3, a) must satisfy this equation
⇒ 2(3) – 3(a) = 5
⇒ 6 – 3a = 5
⇒ – 3a = 5 – 6 = – 1
a = 1/31
∴ a = 1/313
Q5: Determine whether the following system of linear equations is inconsistent or not.
3x – 5y = 20
6x – 10y = -40
Sol: Given
3x – 5y = 20 ……… (i)
6x – 10y = – 40 ………… (ii)
Hence given pair of linear equations are parallel.∴ It is inconsistent.
Short Answer Type Questions
Q1: The father’s age is six times his son’s age. Four years hence, the age of the father will be four times his son’s age. Find the present ages of the son and the father.
Sol:
Let the father's age be y and the son's age be x.
First condition: y = 6x
Second condition: y + 4 = 4 (x + 4)
So, we have 6x + 4 = 4 x + 16
x = 6 and y = 36
Q2: If the lines x + 2y + 7 = 0 and 2x + ky + 18 = 0 intersect at a point, then find the value of k.
Sol: For a unique solution
Substituting the values
Q3: Find the value of k for which the system of equations x + 2y -3 = 0 and ky + 5x + 7 = 0 has a unique solution.
Sol: For a unique solution
Substituting the values
Q4: Find the values of a and b for which the following system of linear equations has an infinite number of solutions:
2x + 3 y = 7
2αx + (a + b) y = 28
Sol: We have
Solving this , we get a = 4 and b = 8
Q5: In a cyclic quadrilateral ABCD, Find the four angles.
a. ∠A = (2 x + 4), ∠B = (y + 3), ∠C = (2y + 10) , ∠D = (4x − 5) .
b. ∠A = (2 x − 1) , ∠ B = (y + 5) , ∠C = (2 y + 15) and ∠D = (4 x − 7)
Sol: a. ∠ A = (2 x + 4) , ∠B = (y + 3), ∠C = (2 y + 10), ∠D = (4 x − 5)
In a cyclic quadrilateral, Opposite angles are supplementary.
∠A + ∠C = 180° and ∠ B + ∠ D = 180°
So, 2x + 4 + 2y + 10 = 180
or x + y = 83 - (1)
y + 3 + 4 x − 5 = 180
or y + 4 x = 182 -(2)
Solving the equations (1) and (2)by Substitution method
x = 33 and y = 50
So Angles are 70°, 53°,110°,127°b. ∠A = (2 x − 1) , ∠B = (y + 5) , ∠C = (2 y + 15) and ∠D = (4 x − 7)
Solving similarly, we get
65°, 55°, 115°, 125°
Long Answer Type Questions
Q1: Draw the graph of 2x + y = 6 and 2x – y + 2 = 0. Shade the region bounded by these lines and the x-axis. Find the area of the shaded region.
Sol: The given system of equations is
2x + y – 6 = 0 ………. (i)
2x – y + 2 = 0 ……… (ii)
Let us write three solutions for each equation of the system in a table.
(i) ⇒ y = 6 – 2x
Table of solutions for 2x + y – 6 = 0Similarly (ii) ⇒ y = 2x + 2
Table of solutions for 2x – y + 2 = 0
Plotting these points of each table of solutions on the same graph paper and joining them with a ruler, we obtain the graph of two lines represented by equations (i) and (ii) respectively as shown in the graph below. Since, the two lines intersect at point P(1, 4). Thus x = 1, y = 4 is the solution of the given system of equations. In the graph, the area is bounded by the lines and the x-axis is ∆PAB which is shaded.Draw PM ⊥ x-axis
Clearly, PM = y-coordinate of P(1, 4) = 4 units
Also, AB = 1 + 3 = 4 units
∴ Area of the shaded region = Area of ∆PAB =× AB × PM=
× 4 × 4 = 8 sq. units.
Q2: Draw the graphs of the following equations:
2x – y = 1, x + 2y = 13
(i) Find the solution of the equations from the graph.
(ii) Shade the triangular region formed by lines and the y-axis.
Sol: 2x – y = 1 …………….. (i)
x + 2y = 13 ………………. (ii)
Let us draw a table of values for (i) and (ii)Plotting these points on the graph paper, we see that the two lines representing equations (i) and (ii) intersect at points (3, 5).
(i) Therefore, (3, 5) is the solution of a given system,
(ii) Also, two lines enclose a triangular region (∆ABC) with a y-axis shaded in the graph.
Q3: A man travels 370 km partly by train and partly by car. If he covers 250 km by train and the rest by car, it takes him 4 hours. But, if he travels 130 km by train and the rest by car, he takes 18 minutes longer. Find the speed of the train and that of the car.
Sol: Let the speed of the train= x km/ hour
Speed of the car = y km/hour
Case I:
Total distance travelled = 370 km
Distance traveled by train = 250 km
Distance travelled by car = (370 – 250) km = 120 km
or 250y + 120x = 4xyor 60x + 125y = 2xyCase II:
Total distance covered = 370 km
Distance covered by train = 130 km
Distance covered by car = (370 -130) km = 240
Time is taken by train =hour
Time is taken by car =hour
According to 2nd condition,= 4 hours 18 minutes
130x+240y=4310
1300y + 2400x = 43xy
or 2400x + 1300y = 43xy
Multiplying equation (i) by 40, we get
or x = 100
From (i) and (iii), we get 60(100) + 125y = 2(100)y
6000 + 125y = 200y
or (200 – 125) y = 6000
or 75y = 6000
or y == 80
Hence, the speeds of the train and car is 100 km/hour and 80 km/hour respectively
Q4: The taxi charges in a city comprise a fixed charge together with the charge for the distance covered. For a journey of 10 km, the charge paid is ₹75 and for a journey of 15 km, the charge paid is ₹110. What will a person have to pay for traveling a distance of 25 km?
Sol: Let fixed charges for taxi be ₹x and charges for covering distance be ₹y per km.
Then, according to the question, we have
x + 10y = 75 ……… (i)
and x + 15y = 110
Subtracting (i) from (ii), we get
5y = 35 ⇒ y = 35 ÷ 5 = 7
Putting y = 7 in (i), we get
x + 10 (7) = 75
⇒ x = 75 – 70 = 5
∴ The person will have to pay for travelling a distance of 25 km = x + 25y = 5 + 25(7) = ₹180.
Q5: Solve the following system by drawing their graph:
(3/2)x – (5/4)y = 6, 6x – 6y = 20.
Determine whether these are consistent, inconsistent, or dependent.
Sol:
Plotting the points and joining by a ruler in each case. Here, we see that the graph of given equations are parallel lines. The two lines have no point in common. The given system of equations has no solution and is, therefore, inconsistent.
|
126 videos|457 docs|75 tests
|
FAQs on Pair of Linear Equations in Two Variables Class 10 Worksheet Maths Chapter 3
| 1. What are the methods to solve a pair of linear equations in two variables? |  |
| 2. How can we determine if a pair of linear equations has no solution, one solution, or infinitely many solutions? |  |
| 3. What is the graphical representation of a pair of linear equations? |  |
| 4. How do you convert a pair of linear equations into their standard form? |  |
| 5. Can you provide a real-life application of pair of linear equations in two variables? |  |

|
Explore Courses for Class 10 exam
|

|
 =
= 

 Substituting the values
Substituting the values


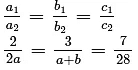


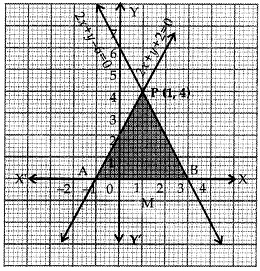 Draw PM ⊥ x-axis
Draw PM ⊥ x-axis × AB × PM=
× AB × PM=  × 4 × 4 = 8 sq. units.
× 4 × 4 = 8 sq. units.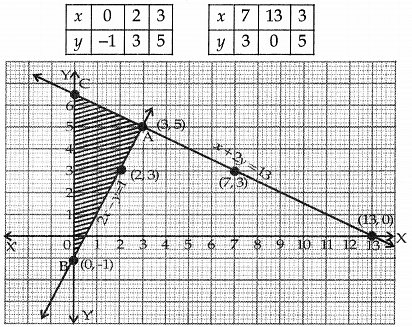

 hour
hour hour
hour = 4 hours 18 minutes
= 4 hours 18 minutes

 = 80
= 80