Understanding Number Series | Science Olympiad Class 6 PDF Download
Introduction
Number Series is a widely asked topic in the Logical Reasoning section of competitive examinations held in India. In these types of questions, there will be a series of numbers given, along with a blank to be filled out. You are given the task of finding out the answer to the blank by figuring out the pattern between the numbers, their predecessor and their successor. It may appear to be a simple task but figuring out the logic behind the pattern is tricky.
What are Number Patterns?
- A list of numbers follows a specific sequence based on a rule. Such as algebraic or arithmetic, geometric, and the Fibonacci pattern.

Arithmetic or Algebraic Patterns
- Using addition or subtraction we can find the missing number in a sequence.
- The difference between the first and second numbers in the below figure is +3.
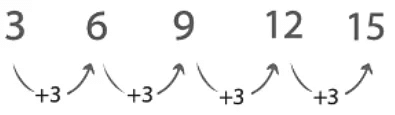
Example: Complete the following number patterns?
5, 10,15 , __, __, __
First Digit = 5
Second Digit = 5 + 5 = 10
Third Digit = 10 + 5 = 15
Clearly, we will add 5 to the preceding digits respectively to find the rest of the digits.
Fourth Digit = 15 + 5 = 20
Similarly , Fifth Digit = 20 + 5 = 25
Sixth Digit = 25 + 5 = 30
Hence the pattern is 5,10,15,20,25,30.

Geometric Series Pattern
- A geometric pattern is a series of numbers formed by multiplying and dividing them.
- Example: Here multiply each term by 2 to get the next term.
2, 4, 8, 16, 32, 64, 128...
Example: Complete the following number patterns?
10, 100,1000 , __, __, __
First Digit = 10
Second Digit = 10 × 10 = 100
Third Digit = 100 × 10 = 1000
Clearly, we will multiply 10 by the preceding digits respectively to find the rest of the digits.
Fourth Digit = 1000 × 10 = 10000
Similarly , Fifth Digit = 10000 × 10 = 100000
Sixth Digit = 100000 × 10 = 1000000
Hence the pattern is 10,100,1000,10000,100000,1000000.
Fibonacci Pattern
- The Fibonacci Pattern is a number sequence in which each consecutive number is obtained by adding the two preceding numbers together.
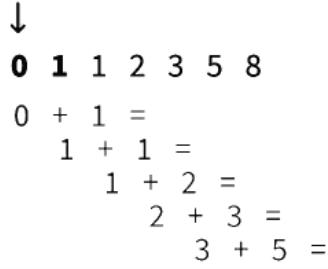
Equal Numbers
- When two or more quantities are exactly the same, we can say they are equal.
- In number patterns, if there is an equal sign(=) in the pattern, then LHS and RHS will have the same numbers.
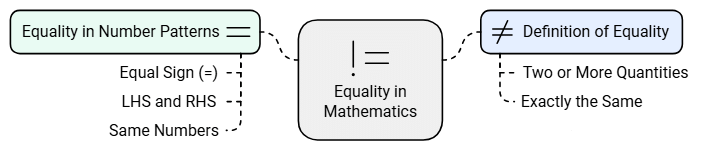
Examples 1: Find the missing numbers in the following pattern: 10, 20, _ = 10, _, 15.
As you can see, there are two numbers in the LHS: 10 and 20.
And in RHS: 10 and 15
As there is an equal sign it means both sides will have the same numbers.
So the missing numbers in the LHS = 15
And, the missing number in the RHS = 20
Numbers in LHS: 10, 20, 15
Numbers in RHS: 10, 20, 15
Numbers in LHS = Numbers in RHS
Therefore LHS = RHS
Examples 2. Check whether LHS is equal to RHS: 15+ _ + _ = 30 + 20 + 15 ?
As you can see, there are three numbers in the RHS: 30 + 20 + 15.
And in LHS only 15
As there is an equal sign it means both sides will have the same numbers.
So the missing numbers will be the numbers that are in the RHS i.e, 30 and 20
So, missing numbers in LHS will be 15 + 30 + 20
If you add both LHS and RHS we get,
LHS: 15 + 30 + 20 = 65
RHS: 30 + 20 + 15 = 65
Therefore LHS = RHS
Palindrome
- Special words/numbers which remain the same when reversed.
- For example, 99 when reversed remains 99; 101, when reversed, remains 101.

Fun with Odd Numbers
- Integers that do not appear in the table of two are known as odd numbers.
- Note: When we add the first n odd numbers, we will get the sum as n × n, where (n) is the number of odd numbers taken at a time.
Example 1: Let us find the sum of the first 3 odd numbers.
First 3 odd numbers: 1,3, 5. Here n = 3
Adding 1 + 3 + 5 we get 9.
Also, we know that When we add first n odd numbers,
we will get the sum as n × n.
Sum of first 3 odd numbers = n × n i.e. 3 × 3 = 9
So, the Sum of the first 3 odd numbers is 9.
Example 2: Find the sum of the first 6 odd numbers.
First 6 odd numbers: 1, 3, 5, 7, 9, 11. Here n = 6
Adding 1 + 3 + 5 + 7 + 9 + 11 we get 36.
Also, we know that when we add first n odd numbers,
we will get the sum as n × n.
Sum of first 6 odd numbers = n × n i.e. 6 × 6 = 36
So, the Sum of the first 6 odd numbers is 36.
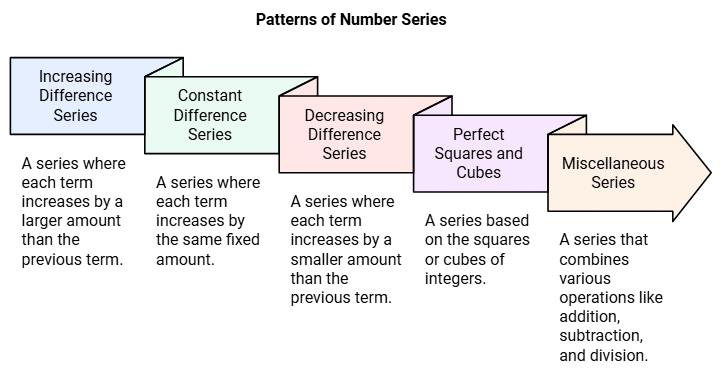
Important Patterns of Number Series
- Series with an increasing difference (most commonly asked)
- Series with a constant difference (the difference will be the same)
- Series with decreasing difference (the difference will be decreasing)
- Perfect squares and cubes of numbers’ series (concept of squares and cubes will be there, either directly or indirectly)
- Miscellaneous series (which may consist of different operations together like addition, subtraction, division, etc.)
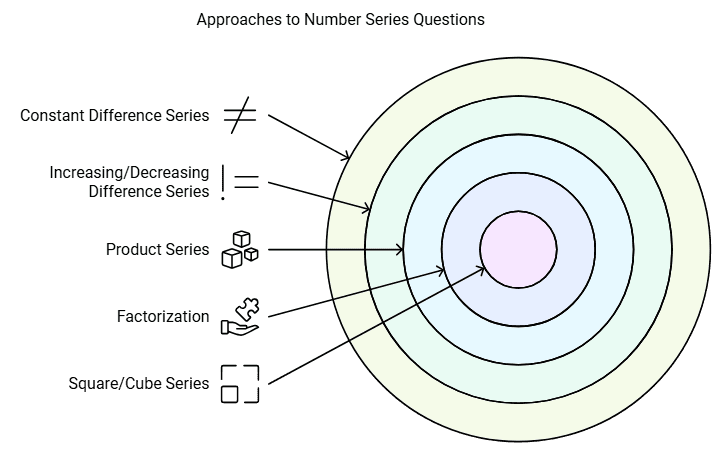
Tips and Tricks to Solve Number Series Questions
The Easiest way to approach number series questions is to observe the difference between the various terms.
Here are some methods and tips you can use to solve number series questions:
- If you observe carefully a constant difference between the different numbers, it means that the question belongs to the series with a constant degree category.
- If you observed carefully the difference between the various numbers it is either increasing or decreasing, then the question belongs to either the series with an increasing difference or the series with decreasing difference respectively.
- In case, you are not able to spot an increasing or decreasing difference between the numbers, try to divide the 2nd term of the series with the first, the 2nd term with the 3rd term and so on. If the answer to the constant division comes as the same number, then this question belongs to the product series.
- In case, none of the above approach works, you can write every term of the question as to the multiplication of 2 factors and try to spot a pattern between the terms.
- If you are not able to spot a pattern and the difference between the terms is decreasing or increasing at an accelerated rate, you can try for the square/cube series.
|
69 videos|145 docs|104 tests
|
FAQs on Understanding Number Series - Science Olympiad Class 6
| 1. What are number patterns and why are they important in mathematics? |  |
| 2. What is a geometric series pattern? |  |
| 3. How does the Fibonacci pattern work? |  |
| 4. What are some tips for solving number series questions effectively? |  |
| 5. Can you explain the significance of equal numbers in number patterns? |  |

















