Short and Long Question: Perimeter and Area | Short & Long Answer Questions for Class 7 PDF Download

Q1: The perimetre is given at 320 m. Calculate the area of the square park.
Ans: According to the given question,
the Perimeter of the square = 320 m
Length of the side of the park = 320/4 = 80 m
Since 4 × length of the side of the park = 320 m
Area of the square park = (length of the park side)² = (80)² = 6400 m².

Q2: Calculate the breadth when the perimetre and length of the rectangular sheet given are 100 cm and 35 cm respectively. Also, calculate the area.
Ans: According to the given question,
Perimetre given is 100 m
Length of the rectangular sheet given is 35 cm
Since perimetre = 2 ( length + breadth )
On applying the formula
100 = 2 (35 + breadth)
100/2 = 35 + breadth
50 = 35 + breadth
50 – 35 = breadth,
Therefore, breath is calculated as 15 cm.
Since we know that the
Area = length × breadth = 35 × 15 = 525 cm²
So, the area of the rectangular sheet is 525 cm²

Q3: Suppose the shape of the wire is a rectangle. The length and breadth of the rectangle are 40 cm and 22 cm respectively. What is going to be the measurements of each side if the wire is bent in the shape of a square? Find out about the shape which encloses more area.
Ans:  The perimetre of the square = perimetre of a rectangle, as given in the question
According to the given question,
the Length of the rectangle = 40 cm
Breadth of the rectangle = 22 cm
Since the perimetre of square and rectangle are equal
2 (length + breadth) = 4 × side
2(40 + 22) = 4 × side
2 × 62 = 4 × side
124 = 4 × side
124/4 = side = 31 cm
Area of the rectangle = length × breadth = 40 × 22 = 880 cm²
Area of the square = side2 = 31 × 31 = 961 cm²
Based on the above values it could be said that the square shape enclosed more area.

Q4: The parallelograms are given below to calculate the area.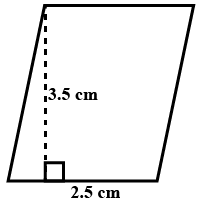

Ans: As given in the figure,
Height = 4 cm, base = 7 cm
Area of the parallelogram = base × height = 7 × 4 = 28 cm²
Height = 3 cm, base = 5 cm
Area of the parallelogram = base × height = 5 × 3 = 15 cm²
Height = 3.5 cm, base = 2.5 cm
Area = 2.5 × 3.5 = 8.75 cm²
Height = 4.8 cm, base = 5 cm
Area = 5 × 4.8 = 24 cm²
Height = 4.4 cm, base =² cm
Area of the parallelogram = 2 × 4.4 = 8.8 cm²

Q5: PQRS is a parallelogram, QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm then calculate the area of the parallelogram PQRS. Calculate QN when PS gave as 8 cm.
Ans: 
SR = 12 cm, QM = 7.6 cm
Area of the parallelogram = length × breadth = SR × QM = 12 × 7.6 = 91.2 cm²
For the second part of the question, calculating QN includes:
Area of the parallelogram = length × breadth
91.2 = PS × QN
91.2 = 8 × QN
QN = 91.2/8 = 11.4 cm

Q6: A rectangular piece of land has a length of 500 m and a breadth of 300 m respectively. Find the area and the cost of the land. The condition given is 1 m2 of the land cost Rs 10,000.
Ans: According to the given question,
The length of the triangle = 500 m
The breadth of the triangle = 300 m
Since the formula for area = length × breadth = 500 × 300 m2 = 150000 m2
If Rs 10,000 is the cost of land of 1m2
Then the cost of 150000 m2 land = 10000 × 150000 = Rs 1500000000

Q7: Calculate the breadth and perimetre of the rectangular plot when the area given is 400 m² and the length given is 22 m.
Ans: According to the given question,
The Area of the given rectangular plot = 440 m2
Length of the plot = 22 m
Applying the formula, area = length × breadth
Therefore, area/length = breadth
Breadth = 440/22 = 20 m
Perimeter of the rectangle will be calculated as = 2(length + Breadth) = 2(22 + 20) = 2 × 42 = 84 m.
So the rectangular plot has a perimetre of 84 m.

Q8: The square park and the rectangular park have the same area. Calculate the breadth of the rectangular park when the side of the rectangular park is 60 m and the length of the rectangular park is 90 m.
Ans: According to the given question,
the Area of the square park = area of the rectangular park
Side of the square park is 60 m
Length of the rectangular park is 90 m
We know the formula that,
Area of the square park = (one of the sides of the square )² = (60)² = 3600 m²
Area of the rectangular park = 3600 m² 
On applying the formula
3600 = 90 × breadth
3600/90 = breadth
40 m = breadth

Q9: The length of the door is 2 m and the breadth is 1 m and it is fitted in a wall. The wall has a length of 4.5 m and a breadth of 3.6 m, what is the cost required for whitewashing the wall when the rate is Rs 20 per m² for whitewashing.
Ans: According to the given question,
The Door has length = 2 m
Door has breadth = 1 m
Wall has length = 4.5 m
Wall has breadth = 3.6 m
Area of the door = length × breadth = 2 × 1 = 2 m²
Area of the wall = length × breadth = 4.5 × 3.6 = 16.2 m²
The area for whitewashing = 16.2 – 2 = 14.2 m²
The cost of the whitewashing 1 m2 area = 20 Rs
Cost of whitewashing the area of 14.2 m2 = 14.2 × 20 = 284 Rs