Short and Long Question: Visualising Solid Shapes | Short & Long Answer Questions for Class 7 PDF Download

Q1: Give (i) an oblique sketch and (ii) an isometric sketch for each of the following:
(a) A cuboid of dimensions 5 cm,3 cm and 2 cm. (Is your sketch unique?)
(b) A cube with an edge 4 cm long.
Ans: The sketch is not unique. Because, any of the three faces can be placed front and the view could be different eventhough the object is the same.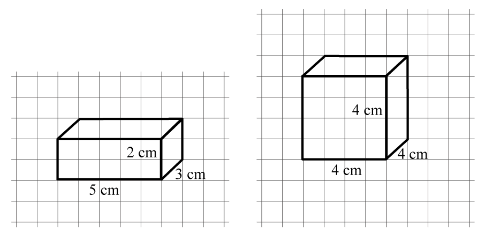

Q2: Write number of edges, faces and vertices of cube, cuboid, cone, cylinder, sphere, triangular pyramid, rectangular and prism.
Ans:
→Cube
No. of edges=12
No. of faces=6
No. of vertices=8
→Cuboid
No. of edges=12
No. of faces=6
No. of vertices=8
→Cone
No. of edges=0
No. of faces=1
No. of vertices=0
→Cylinder
No. of edges=0
No. of faces=2
No. of vertices=0
→Sphere
No. of edges=0
No. of faces=0
No. of vertices=0
→Triangular pyramid
No. of edges=6
No. of faces=4
No. of vertices=4
→Rectangular prism
No. of edges=9
No. of faces=5
No. of vertices=6

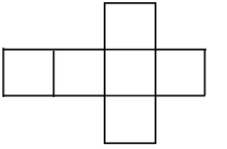
Q3: Draw nets for each of the following polyhedrons:

Ans: Net for cube is shown in the above figure.

Q4: Name any four objects from your environment, which have the form of a cuboid.
Ans: The four objects from the environment which have the form of a cuboid are as follows and the pictures of the objects are shown in the above image:

• A storage box 
• A cupboard 
• A book
•  A duster

Q5: Fill in the blanks to make the following statements true:
________edges of a cube (or cuboid) meet at each of its vertices.
Ans: 
A cube or cuboid is a 3D object having 6 flat faces, 12 edges and 8 vertices.
A vertex is the point where three edges meet.
Hence, three edges of a cube (or cuboid) meet at each of its vertices.

Q6: Write down the number of edges of a Triangular prism
Ans: A triangular prism has 9 edges.
Namely AB,BC,CD,DA,EF,FC,FD,EA,BE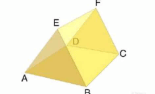

Q7: Write the name of
(a) Vertices  (b) edges  (c) Faces of the prism shown in figure

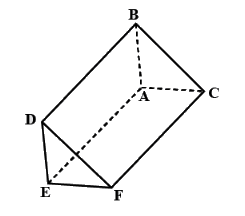Ans: 
Finding the vertices, edges and faces of a prism:
(a). Points at which sides of a polyhedron made up of line segments intersect are known as vertices.
By using the above definition, A, B, C, D, E and F are the vertices.
(b). Line segments from which formation of a polyhedron takes place are known as edges.
Hence in the given figure, AB, BC, CA, ED, DF, FE, BD, CF and AE are the edges.
(c). Two dimensional surfaces in a three-dimensional figure are known as faces.
In the given prism, DBCF, DEAB, EFCA, EDF and ABC are the faces of prism.

Q8: State true or false:
A cone has one vertex.
A. True
B. False
Ans: We know that vertex is a point where two or more line segments meet.
The above figure shows a cone. It has 1 vertex, 1 curved edge, 1 flat face and $1$$ curved face.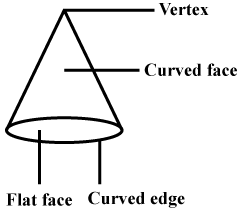
Hence, the given statement is true.

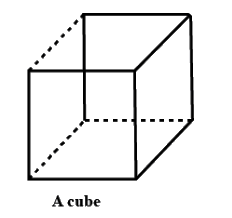
Q9: A cube has 6 faces, 12 edges and 8 vertices.
A. True
B. False
Ans: A cube is a 3D object, like shown in the above diagram.
It has 6 square-shaped faces, 12 edges and 8 corners or vertices.

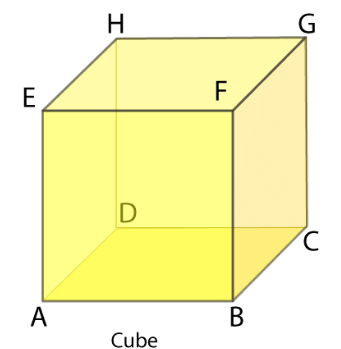Hence, the given statement is true.

Q10: For each of the following solids, identify the front, side and top views and write it in the space provided.

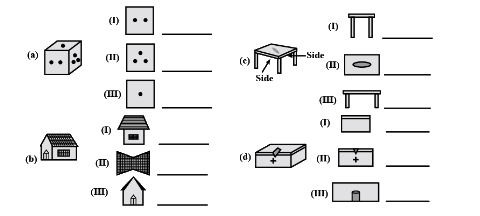
Ans:
From observation we can see that in:
figure (a):
(i) is a front view,
(ii) is a side view, and
(iii) is a top view
figure (b):
(i) is a side view,
(ii) is a top view, and
(iii) is a front view
figure (c):, both horizontal view are side view, so
(i) is a side view,
(ii) is a top view, and
(iii) is a side view
figure (d):
(i) is a side view,
(ii) is a front view, and
(iii) is a top view

Q11: A polyhedron can have 3 faces.
A. True
B. False
Ans: The given statement is false.
because, tetrahedron is a polyhedron with the minimum number of faces equal to 4.
So, polyhedron cannot have 3 faces.

Q12: In a three-dimensional shape, diagonal is a line segment that joins two vertices that do not lie on the _____ face.
Ans: In a three-dimensional shape, diagonal is a line segment that joins two vertices that do not lie on the same face.
Because, diagonal is line joining extreme corners of 3 dimensional shape.

Q13: If the sum of the number of vertices and faces in a polyhedron is 14, then the number of edges in the shape is ______.
Ans: 
Euler's Formula for any polyhedron is, F + V − E = 2.
Where, F = Faces and V = Vertices and E =  Edges.
Therefore, it is given that,
F + V = 14
⇒ 14 − E = 2
⇒ E = 12
So, If the sum of the number of vertices and faces in a polyhedron is 14, then the number of edges in the shape is 12.

Q14: The net of a rectangular prism has _______ rectangles. (Hint: Every square is a rectangle but every rectangle is not a square.)
Ans: Rectangular prism has two rectangles at opposite ends and 4 rectangles on each side connecting end rectangles.

So, in total has 6 rectangles.

Q15: Every cylinder has 2 opposite faces as congruent circles, so it is also a prism.
A. True
B. False
Ans: The given statement is false.
Prism is a polyhedron.
But cylinder has non-straight line as its edges i.e circles.
So, it is not a polyhedron and hence it is not a prism.