Class 10 Maths Chapter 11 Practice Question Answers - Area Related to Circles
Q1. The length of an arc of a sector of a circle of radius r units and of centre angle θ is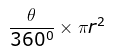
(a) True
(b) False
(c) Neither
(d) Either
Ans: b
Sol: Length of arc subtending angle 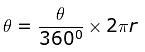 Note that area will have the dimension of square of length. So,
Note that area will have the dimension of square of length. So, 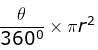 cannot be the length.
cannot be the length.
Q2. If the sum of the circumferences of two circles with radii R1 and R2 is equal to the circumference of a circle of radius R, then
(a) R1 + R2 = R
(b) R1 + R2 > r
(c) R1 + R2 < r
(d) Nothing definite can be said about the relation among R1 ,R2 and R.
Ans: (b)
Sol:
The circumference of circle with radius R1= 2πR1
and the circumference of circle with radius R2 = 2πR2
∴ The Sum of Circumferences, Sum=2π(R1+ R2)
Again the circumference of circle with radius R=2πR.
∴ By given condition,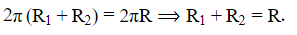
Q3. Find the area of shaded portion, where the length of it is 14 units and radius of the upper semicircle is 7 units.
(a) 196
(b) 98
(c) 200
(d) None
Ans: (a)
Sol:
Requried area of figure = Area of shaded portion
If we substract area of semi circle from area of rectangle & then add the area of upper semi circle, we get the net area or alternatively, if we calculate the area of rectangle, we get the net area = l x b
= 14 x 14
=196
Q4. Length of an arc of a sector of a circle with radius r and angle with degree measure θ is 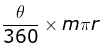
m is
Sol:
The whole circle of 360º makes arc length of 2πr
Thus angle of θ will make a length = 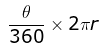
Q5. If the sector of a circle of diameter 10 cm subtends an angle of 144º at the centre, then the length of the arc of the sector is
(a) 2π cm
(b) 4π cm
(c) 5π cm
(d) 6π cm
Ans: (b)
Sol: Given, diameter =10 cm, θ=144º
Length of an arc of a circle 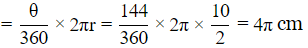
Hence, option B is correct.
Q6. ABCD is a trapezium of area 24.5 sq. cm. In it, AD∥BC,∠DAB=90º, AD=10 cm and BC=4 cm. If ABE is a quadrant of a circle, find the area of the shaded region.
(Take π = 22/7)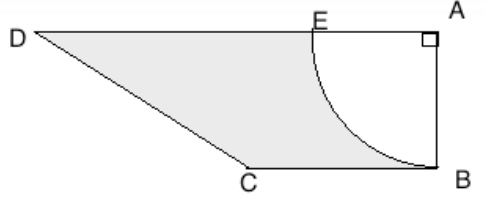
Sol:
Given:
AD=10 cm
BC=4 cm
Area of trapezium =24.5 cm2
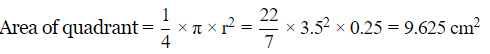
The area of shaded region = Area of trapezium – Area of given quadrant
The area of shaded region =24.5–9.625=14.875 cm2
Q7. Take π=3.14, the circumference of a circle with diameter = 1.2 m is 3.768 m. If true then enter 1 and if false then enter 0.
Sol:
Given that,
Diameter of a circle is 1.2 m.
The circumference of the circle is 3.768 m.
We know that, circumference =2πr or πd.
=3.14×1.2[ given π=3.14 ]
=3.768 m
So, it is true that the circumference of the circle is 3.768 m.
Hence, 1 is the answer.
Q8. If the area of a circle is 154 cm2 , then its circumference in cm is
Sol:
Area of the circle =πr2
Circumference of the circle 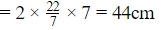
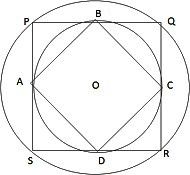
Q9. The figure below shows two concentric circles with centre O. PQRS is a square inscribed in the outer circle. It also circumscribes the inner circle, touching it at point B,C,D and A. The ratio of the perimeter of the outer circle to that of polygon ABCD is
(a) π/4
(b) 3π/4
(c) π/2
(d) π
Ans: (c)
Sol:
Let the radius of the outer circle be r.
∴ perimeter of outer circle = 2πr
But OQ=BC=r [diagonals of the square BQCO]
∴ Perimeter of Square ABCD =4r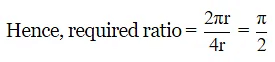
Q10. The figure is shown in a rectangle topped with a semicircle. The base of the rectangle is one-third its height. If h is the height of the rectangle, what is the area of the figure?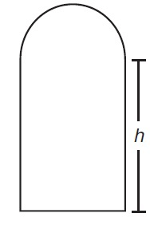 (a)
(a) 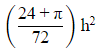
(b) 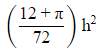
(c) 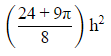
(d) 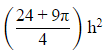
Ans: (a)
Sol:
Given that:
The height of the rectangle is equal to h.
The base of the rectangle = h/3
The base of the rectangle = Diameter of the semicircle
∴ Radius of the circle = h/6
Now,
Area of the figure = Area of the rectangular part + Area of the semicircular part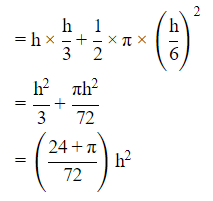
Hence, option A is correct.
|
127 videos|584 docs|79 tests
|
















