Class 9 Maths Chapter 8 Question Answers - Quadrilaterals

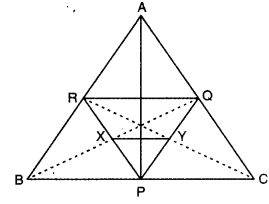
Q1: In the figure, P, Q and R are the mid-points of the sides BC, AC and AB of ΔABC. If BQ and PR intersect at X and CR and PQ intersect at Y, then show that XY = 1/4 BC.

Ans:
Here, in ΔABC, R and Q are the mid-points of AB and AC respectively.
∴ By using mid-point theorem, we have
RQ || BC and RQ = 1/2 BC
∴ RQ = BP = PC [∵ P is the mid-point of BC]
∴ RQ || BP and RQ || PC
In quadrilateral BPQR
RQ || BP, RQ = BP (proved above]
∴ BPQR is a parallelogram. [∵ one pair of opp. sides is parallel as well as equal]
∴ X is the mid-point of PR. [∵ diagonals of a ||gm bisect each other]
Now, in quadrilateral PCQR
RQ || PC and RQ = PC [proved above)
∴ PCQR is a parallelogram [∵ one pair of opp. sides is parallel as well as equal]
∴ Y is the mid-point of PQ [∵ diagonals of a ||gm bisect each other]
In ΔPQR
∴ X and Y are mid-points of PR and PQ respectively.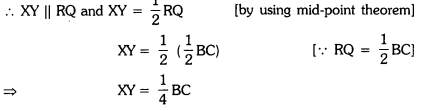


Q2: In ΔABC, AB = 8 cm, BC = 9 cm and AC = 10 cm. X, Y and Z are mid-points of AO, BO and CO respectively as shown in the figure. Find the lengths of the sides of ΔXYZ.

Ans:
Here, in ΔABC, AB = 8 cm, BC = 9 cm, AC = 10 cm.
In ΔAOB, X and Y are the mid-points of AO and BO.
∴ By using mid-point theorem, we have
XY = 1/2 AB = 1/2 x 8 cm = 4 cm
Similarly, in Δ𝜏BOC, Y and Z are the mid-points of BO and CO.
∴ By using mid-point theorem, we have
YZ = 1/2 BC = 1/2 x 9cm = 4.5 cm
And, in Δ𝜏COA, Z and X are the mid-points of CO and AO.
∴ ZX = 1/2 AC = 1/2 x 10 cm = 5 cm
Hence, the lengths of the sides of ΔXYZ are XY = 4 cm, YZ = 4.5 cm and ZX = 5 cm.

Q3: ABCD is a parallelogram. If the bisectors DP and CP of angles D and C meet at P on side AB, then show that P is the mid-point of side AB.
Ans:

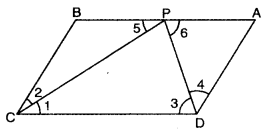
Since DP and CP are angle bisectors of ∠D and ∠C respectively.
: ∠1 = ∠2 and ∠3 = ∠4
Now, AB || DC and CP is a transversal
∴ ∠5 = ∠1 [alt. int. ∠s]
But ∠1 = ∠2 [given]
∴ ∠5 = ∠2
Now, in ABCP, ∠5 = ∠2
⇒ BC = BP … (I) [sides opp. to equal ∠s of a A]
Again, AB || DC and DP is a transversal.
∴ ∠6= ∠3 (alt. int. Δs]
But ∠4 = ∠3 [given]
∴ ∠6 = ∠4
Now, in ΔADP, ∠6 = ∠4
⇒ DA = AP …. (ii) (sides opp. to equal ∠s of a A]
Also, BC = DA… (iii) (opp. sides of parallelogram)
From (i), (ii) and (iii), we have
BP = AP
Hence, P is the mid-point of side AB.

Q4: In the figure, ΔBCD is a trapezium in which AB || DC. E and F are the mid-points of AD and BC respectively. DF and AB are produced to meet at G. Also, AC and EF intersect at the point O. Show that :
(i) EO || AB
(ii) AO = CO

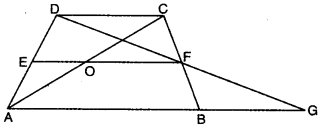
Ans:
Here, E and F are the mid-points of AD and BC respectively.
In ΔBFG and ΔCFD
BF = CF [given]
∠BFG = ∠CFD (vert. opp. ∠s]
∠BGF = ∠CDF (alt. int. ∠s, as AB || DC)
So, by using AAS congruence axiom, we have
ΔBFG ≅ ΔCFD
⇒ DF = FG [c.p.c.t.)
Now, in ΔAGD, E and F are the mid-points of AD and GD.
∴ By mid-point theorem, we have
EF || AG
or EO || AB
Also, in ΔADC, EO || DC
∴ EO is a line segment from mid-point of one side parallel to another side.
Thus, it bisects the third side.
Hence, AO = CO

Q5: PQRS is a square and ∠ABC = 90° as shown in the figure. If AP = BQ = CR, then prove that ∠BAC = 45°

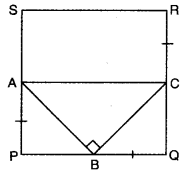
Ans:
Since PQRS is a square.
∴ PQ = QR … (I) [∵ sides of a square are equal]
Also, BQ = CR … (ii) [given]
Subtracting (ii) from (i), we obtain
PQ – BQ = QR – CR
⇒ PB = QC … (iii)
In Δ𝜏APB and Δ𝜏BQC
AP = BQ[given
∠APB = ∠BQC = 90°](each angle of a square is 90°)
PB = QC (using (iii)]
So, by using SAS congruence axiom, we have
ΔAPB ≅ ΔBQC
∴ AB = BC [c.p.c.t.]
Now, in ΔABC
AB = BC [proved above]
∴ ∠ACB = ∠BAC = x° (say) [∠s opp. to equal sides]
Also, ∠B + ∠ACB + ∠BAC = 180°
⇒ 90° + x + x = 180°
⇒ 2x° = 90°
x° = 45°
Hence, ∠BAC = 45°

Q6: In the given figure, AE = DE and BC || AD. Prove that the points A, B, C and D are concyclic. Also, prove that the diagonals of the quadrilateral ABCD are equal.

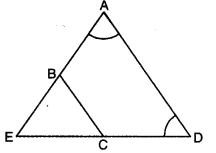
Ans:
Since AE = DE
∠D = ∠A …. (i) [∵ ∠s opp. to equal sides of a Δ]
Again, BC || AD
∠EBC = ∠A …. (ii) (corresponding ∠s]
From (i) and (ii), we have
∠D = ∠EBC …. (iii)
But ∠EBC + ∠ABC = 180° (a linear pair]
∠D + ∠ABC = 180° (using (iii)]
Now, a pair of opposite angles of quadrilateral ABCD is supplementary
Thus, ABCD is a cyclic quadrilateral i.e., A, B, C and D’are concyclic. In ΔABD and ΔDCA
∠ABD = ∠ACD [∠s in the same segment for cyclic quad. ABCD]
∠BAD = ∠CDA [using (i)]
AD = AD (common]
So, by using AAS congruence axiom, we have
ΔABD ≅ ΔDCA
Hence, BD = CA [c.p.c.t.]