Class 9 Maths Chapter 5 Practice Question Answers - Introduction To Euclid’s Geometry
Q1: Which Euclid's postulate led to the discovery of several other geometries while attempting to prove it using other postulates and axioms
(a) Fifth Postulate
(b) First Postulate
(c) Second Postulate
(d) Third Postulate
Ans: (a)
Attempts to prove Euclid's Fifth Postulate using other postulates and axioms led to the discovery of several others geometries
Q2: Euclid stated that if equals are subtracted from equals, the remainders are equals in the form of:
(a) an axiom
(b) a postulate
(c) a definition
(d) a proof
Ans: (a)
The above statement is Euclid's third axiom which states that If equals are subtracted from equals, the remainders are equal. So, A is correct.
Q3: John is of the same age as Mohan. Ram is also of the same age as Mohan. State the Euclid's axiom that illustrates the relative ages of John and Ram.
(a) First axiom
(b) Second axiom
(c) Third axiom
(d) Fourth axiom
Ans: (a)
Given that,
John's age = Mohan's age &
Ram's age = Mohan's age.
Euclid's first axiom states that, things which are equal to the same thing, are equal to one another.
So, by the first axiom of Euclid,
John's age = Ram's age.
Hence, Euclid's first axiom is applicable here.
Q4: Euclid's stated that all right angles are equal to each other in the form of :
(a) an axiom
(b) a definition
(c) a postulate
(d) a proof
Ans: (c)
One of Euclid's five postulates is:
All right angles are CONGRUENT.
So, the correct option is C.
Q5: The things which are double of same thing are :
(a) equal
(b) halves of same thing
(c) unequal
(d) double of the same thing
Ans: (a)
According to an Euclidian axiom,
The things which are double of the same things are equal to one another.
Example: if 2x=2y, then x=y.
Hence, option A is correct.
Q6: Euclidean geometry is valid only for curved surfaces.
(a) True
(b) False
(c) Sometimes True
(d) Data Insufficient
Ans: (b)
Euclid's postulates:
⇒ A straight line can be drawn joining any two points.
⇒ A straight line segment can be extended indefinitely in a straight line.
⇒ A circle can be drawn having the segment as radius and one endpoint as center.
⇒ All right angles are congruent and equal.
⇒ Parallel postulate.
Hence, we can observe that euclidian geometry is valid for 2-dimensional geometrical figures.
Q7: Axioms are assumed
(a) universal truths in all branches of mathematics
(b) universal truths specific to geometry
(c) theorems
(d) definitions
Ans: (a)
From time immemorial, axioms have been acquired by man through the day to day experiences.
No mathematical deduction is needed to prove them.
Practically they are starting points of reasoning.
So axioms are assumed universal truths in all branches of mathematics.
Q8: The things which coincide with one another are:
(a) equal to another
(b) unequal
(c) double of same thing
(d) Triple of same things
Ans: (a)
According to Euclid's postulates, equal things coincide with each other.
Hence, A is correct.
Q9: The boundaries of the solids are called curves.
(a) True
(b) False
(c) Ambiguous
(d) Data Insufficient
Ans: (b)
The boundaries of the solids are called surfaces.
While the boundaries of the surfaces are called curves.
Q10: The total number of propositions in the Elements book written by Euclid are
(a) 465
(b) 460
(c) 13
(d) 55
Ans: (a)
Elements is the book written by a mathematician Euclid's and it has 465 propositions , 131 definitions 5 postulates of Euclid's and 5 common notions are written
Therefore, there are 465 propositions in the elements.
Q11: In figure A and B are the centres of the two intersecting circles.
With the help of Euclid's first axiom, state the type of ΔABC.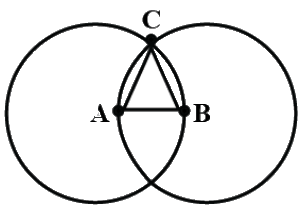 (a) An equilateral triangle.
(a) An equilateral triangle.
(b) An isosceles triangle
(c) A scalene triangle
(d) A right angle triangle
Ans: (a)
From the above figure, AB and AC are the radii of the circle on the left, where C is the point of intersection of the two circles.
Similarly, BA and BC are the radii of the circle on the right, where C is the point of intersection of the two circles.
We know, AB=AC and BC=AB, thus by Euclid's first axiom, AC=BC.
Hence AC=BC=AB which makes triangle ABC an equilateral triangle.
Q12: Read the following axioms:
(i) Things which are equal to the same thing are equal to one another.
(ii) If equals are added to equals, the wholes are equal.
(iii) Things which are double of the same thing are equal to one another.
Check whether the given system of axioms is consistent or inconsistent.
(a) Consistent
(b) Inconsistent
(c) Either
(d) Neither
Ans: (a)
This set of axiom is consistent.
(i) If a=b and b=c then a =c
(ii) If a = b and c = d then a+ b =c +d
(iii) If x = 2y and z = 2y then x = z
Q13: Two distinct ________ lines cannot be parallel to the same line.
(a) Intersecting
(b) Non-intersecting
(c) Parallel
(d) None of these
Ans: (a)
Two intersecting lines cannot be parallel to same line as this statement is equivalent to Euclid's fifth postulate.
Q14: Euclid's second axiom is
(a) the things which are equal to the same thing are equal to one another
(b) if equals be added to equals, the wholes are equal
(c) if equals be subtracted from equals, the remainders are equals
(d) things which coincide with one another are equal to one another
Ans: (b)
Euclid's second axiom can be stated as any terminated straight line can be projected indefinitely or it can be stated as if equals be added to equals, the wholes are equal.
Q15: Euclid stated that all right angles are equal to one another in the form of a/an ..........
(a) Axiom
(b) Defination
(c) Postulate
(d) Proof
Ans: (c)
- A straight line may be drawn from any point to any other point.
- A terminated line (line segment) can be produced indefinitely.
- A circle may be described with any centre and any radius.
- All right angles are equal to one another.
- If a straight line falling on two straight lines makes the interior angles on the same side of it, taken together less than two right angles, then the the two straight lines if produced indefinitely, meet on that side on which the sum of angles is taken together less than two right angles. Euclid used the term postulate for the assumptions that were specific to geometry and otherwise called axioms. A theorem is a mathematical statement whose truth has been logically established.
Q16: Using Euclid's division algorithm, find whether the pair of numbers 231,396 are coprime or not.
Ans: ⇒396=1×231+165
⇒231=1×165+66
⇒165=2×66+33
⇒66=2×33+0
∴ The HCF of 231,396 is 33 not 1, so they are not co-prime.
Q17: Construct ΔPQR such that ∠R = 100º , QR = RP = 5.4cm.
Ans: Draw a line, from one end, make angle 100º by the protector and mark it as ∠R. From R mark point at 5.4cm on both lines and join the points mark them as P and Q.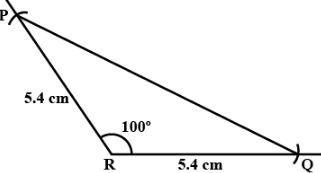
Q18: What is the need of introducing axioms?
Ans: Earlier Greek Mathematician has to depends on some factors like point, straight lines, plane etc. But this was not enough to prove everything. They had to assembled certain statement whose validity was absolute, Thus there was a need of introducing axioms.
Q19: Point C is the mid-point of line segment AB, prove that every line segment has one and only one mid-point.
Ans: AC = BC ... (i)
If possible, let D be another mid-point of AB.
AD = DB ... (ii)
Subtracting (ii) from (i)
AC – AD = BC – DB
DC = −DC (∵AC−AD = DC and CB − DB = −DC)
DC + DC = 0
2DC = 0
DC = 0
So, C and D coincide.
Thus, every line segment has one and only one mid-point.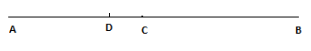
Q20: It is possible to draw a straight line from any point to any other point. The given statement is _________.
(a) theroem
(b) conjectures
(c) postulate
(d) operation
Ans: (c)
It is possible to draw a straight line from any point to any other point. A postulate is a statement that is accepted without proof. Axiom is another name for a postulate.
For example, if you know that Pam is five feet tall and all her siblings are taller than her, you would believe her if she said that all of her siblings are at least five foot one. Pam just stated a postulate, and you just accepted it without grabbing a tape measure to verify the height of her siblings.
|
40 videos|471 docs|57 tests
|





















