Class 9 Maths Chapter 8 Practice Question Answers - Quadrilaterals
Q1: The value of x in the given diagram is ?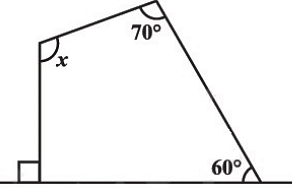
(a) 130o
(b) 140o
(c) 150o
(d) 160o
Ans: (b)
Step 1: Find x using angle sum property.
We know, by angle sum property, the sum of angles of a quadrilateral is 360 o .
The given angles are 70o , 60o , 90o , x.
[Linear pairs are supplementary]
Then, 70º + 60º + 90º + x = 360º.
Therefore, the unknown angle is:
⇒ 360º − (70º + 60º + 90º) = x
⇒ x = 360º −220º = 140º.
Therefore, the unknown angle is x = 140º.
Hence, option B is correct.
Q2: Can all the four angles of a quadrilateral be obtuse angle?
(a) Yes
(b) No
(c) May be
(d) Cannot be determined
Ans: (b)
⇒ An obtuse angle is greater than 90o and by angle sum property, the sum of all four angles of a quadrilateral is 360o.
⇒ If we take all four angles greater than 90o then, there sum will be obviously greater than 360o.
Hence, all the four angles of a quadrilateral cannot be obtuse.
Therefore, option B is correct.
Q3: Can a quadrilateral ABCD be a parallelogram for the following condition? (Enter 1 for True and 0 for False)AB = DC = 8 cm, AD = 4 cm and BC= 4.4 cm.
Ans: The answer is false.
Its given that AB = DC = 8cm,
⇒ AD = 4cm and BC = 4.4cm
To form a parallelogram the opposite sides should be of same length here, AD=BC
Hence, the answer is False.
Q4: All rhombuses are parallelograms?
(a) True
(b) False
(c) Ambiguous
(d) Data Insufficient
Ans: (a)
Opposite sides of a parallelogram are equal but all sides of a rhombus are equal. So, rhombus is a parallelogram but parallelogram is not a rhombus.
Q5: Find the unknown angle in the figure.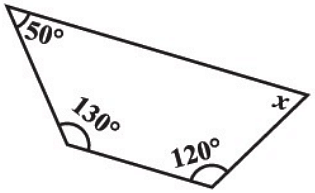 (a) 40º
(a) 40º
(b) 50º
(c) 60º
(d) 70º
Ans: (c)
We know, by angle sum property, the sum of angles of a quadrilateral is 360o.
The given angles are 50º , 130º, 120º , x.
Then, 50º +130º +120º + x = 360º.
Therefore, the unknown angle is:
⇒ 360º −(50º +130º +120º) = xº
⇒ xº = 360º − 300º = 60º.
Therefore, the unknown angle is xº = 60º. Hence, option C is correct.
Q6: If two adjacent angles of a parallelogram are in the ratio of 2:3 find all the angles of the parallelogram.
Ans: Let parallelogram be PQRS
Two adjacent angles of parallelogram are in ratio 2:3
Let ∠P = 2x
∠Q = 3x
∠P + ∠Q = 2x + 3x = 5x
180 = 5x
x = 180/5 = 36
∠P = 2x = 2 × 36 = 72
∠Q = 3x = 3 × 36 = 108
∠P = ∠R(opposite angles)
∠R = 72º
∠Q and ∠S are equal
∠S = 108º
∴angles of parallelogram are 72º, 108º, 720 and 108º
Q7: The angles of a quadrilateral are of the measures 120o , 90o, 72o and xo , then find x.
Ans: We know, by angle sum property, the sum of angles of a quadrilateral is 360o.
The given angles are 120º, 90º, 72º,x.
Then, 120º + 90º + 72º + x = 360º.
⇒ x = 360º −(120º + 90º + 72º)
⇒ x = 360º − 282º = 78º.
Therefore, the unknown angle is x = 78º.
Q8: Angles of a quadrilateral are in the ratio 3 : 6 : 8 : 13. The largest angle is :
(a) 178º
(b) 90º
(c) 156º
(d) 36º
Ans: (c)
Given ratio of angles are 3:6:8:13.
Let the angles be 3x ,6x ,8x ,13x.
By angle sum property, the sum of all angles of quadrilateral is 360º.
So, 3x + 6x + 8x + 13x = 360º
⟹ 30x = 360º
⟹ x = 360º/30
⟹ x = 12º.
Then, 3x = 3 × 12o = 36o ,
6x = 6 × 12o = 72o ,
8x = 8 × 12o = 96o
and 13x = 13 × 12o = 156o.
Hence, the largest angle is 156o.
Therefore, option C is correct.
Q9: Three angles of a quadrilateral are of the measure 130º, 82º , 40º . Find the measure of the fourth angle.
Ans: We know, by angle sum property, the sum of angles of a quadrilateral is 360o.
The given angles are, 130º , 82º , 40º.
Let the fourth angle be xº.
Then, 130º + 82º + 40º + xº = 360º .
⇒ 360º −(130º +82º +40º)= xº
⇒ xº = 360º −252º =108º.
Therefore, the fourth angle is xº =108º.
Q10: The angles of a quadrilateral are in the ratio 2:3:5:8. Find the smallest angle of the quadrilateral.
Ans: Given ratio of angles of quadrilateral ABCD is 2:3:5:8
Let the angles of quadrilateral ABCD be 2x,3x,5x,8x, respectively.
We know, by angle sum property, the sum of angles of a quadrilateral is 360º.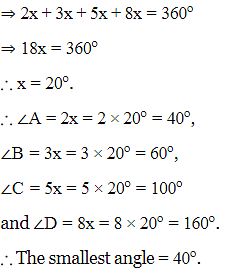
Q11: One angle of a quadrilateral is of 108º and the remaining three angles are equal. Find each of the three equal angles.
(a) 64o
(b) 74o
(c) 84o
(d) 94o
Ans: (c)
We know, by angle sum property, the sum of angles of a quadrilateral is 360º.
Given, one angle is 108º and remaining three angles are equal.
Let the remaining angles be xº, yº, zº .
Since they are equal, xº + yº + zº = xº + xº + xº = 3xº.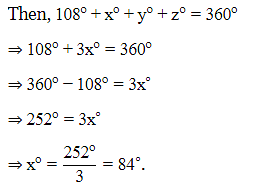
Therefore, each of the three remaining angle is xo = 84o.
Hence, option C is correct.
Q12: D and E are the mid-points of the sides AB and AC of ABC and O is any point on side BC.O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is:
(a) a square
(b) a rectangle
(c) parallelogram
(d) quadrilateral whose opposite angles are supplementary
Ans: (d)
Given:
ABC is a triangle, D & E are the respective mid points of AB &AC.
O is any point on BC, P & Q are mid points of OB & OC respectively.
To find:
Type of quadrilateral of DEQP.
In ΔABC,D&E are the respective mid points of AB & AC.
∴DE∥(BCorPQ) ....(1)
Again in ΔABO,P&D are the respective mid points of AB & BO
∴DP∥AO ... (2)
Similarly, in ΔACO,EQ∥AO ...(3)
∴ From (2) & (3), we get
DP∥EQ ... (4)
∴ From (1) & (4), we have
DE∥PQ and DP∥EQ
So, DEQP is parallelogram.
Hence, option D.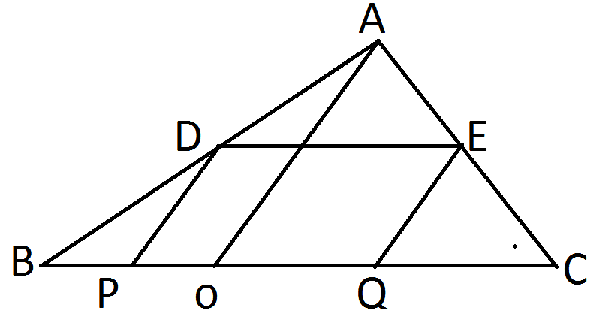
Q13: Three angles of a quadrilateral are 75º ,90º and 75º. The measure of fourth angle is?
(a) 90º
(b) 95º
(c) 105º
(d) 120º
Ans: (d)
We know, by angle sum property, the sum of angles of a quadrilateral is 360º.
The given angles are, 75º, 90º,75º.
Let the fourth angle be xº.
Then, 75º + 90º +75o + xo = 360o.
⇒ 360o − (75o + 90o + 75o)= x∘
⇒ xo = 360o − 240o = 120º.
Therefore, the fourth angle is xº =120º.
Hence, option D is correct.
Q14: Can all the angles of a quadrilateral be acute angles?
(a) Yes
(b) No
(c) May be
(d) Cannot be determined
Ans: (b)
Let us take a qudrilateral ABCD with BD as diagonal.
In ΔABD we have,
∠ADB +∠ABD + ∠DAB = 180º .......(i)
And in ΔDBC we have
∠DCB+∠CBD+∠BDC=180 O ......(ii)
Adding (i) & (ii), we get,
∠ADB+∠ABD+∠DAB+∠DCB+∠CBD+∠BDC = 360º
⟹∠A+∠B+∠C+∠D = 360º
So, the sum of the angles of a quadrilateral is 360 O .....(iii).
Now, if the angles are acute then ∠A < 90º ,∠B<90º ,∠C<90º ,∠D<90º
⟹∠A+∠B+∠C+∠D<90º +90º +90º +90º
⟹∠A+∠B+∠C+∠D<360º.
But this does not comply with (iii) . Therefore, all the angles of a quadrilateral cannot be acute angles. Hence, option B is correct.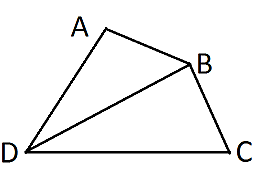
Q15: Can the angles 110º , 80o , 70 º and 95º be the angles of a quadrilateral?
(a) Yes
(b) No
(c) May be
(d) Cannot be determined
Ans: (b)
We know, by angle sum property, the sum of angles of a quadrilateral is 360º.
The given angles are 110º , 80º, 70º, 95º.
Then, 110º + 80º + 70º + 95º .
=190º + 165º
= 355º ≠ 360º.
Therefore, the given angles are not the angles of a quadrilateral. Hence, option B is correct.
Q16: The figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only if,
(a) ABCD is a rhombus
(b) diagonals of ABCD are equal
(c) diagonals of ABCD are equal and perpendicular
(d) diagonals of ABCD are perpendicular.
Ans: (c)
In given figure,
ABCD is a quadrilateral and P,Q,R & S are mid-pints of sides AB,BC,CD and DA respectively. Then, PQRS is a square.
∴PQ=QR=RS=PS --------- (1)
and PR=SQ
But PR=BC and SQ=AB
∴AB=BC
Thus, all sides of quadrilateral ABCD are equal.
Hence, quadrilateral ABCD is either a square or a rhombus.
Now, in △ADB,
By using Mid-point theorem,
SP∣∣DB;SP= 1/2 DB ------ (2)
Similarly in △ABC,
PQ∣∣AC;PQ= 1/2 AC ----- (3)
From equation (1),
PS = PQ
From (2) and (3),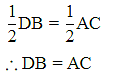
Thus, diagonals of ABCD are equal and therefore quadrilateral ABCD is a square. So, diagonals of quadrilateral also perpendicular.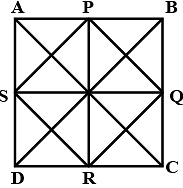
Q17: The quadrilateral formed by joining the mid-points of the sides AB,BC,CD,DA of a quadrilateral ABCD is
(a) a trapezium but not a parallelogram
(b) a quadrilateral but not a trapezium
(c) a parallelogram only
(d) a rhombus
Ans: (c)
Given quadrilateral formed By joining mid points of the sides AB,BC,CD,DA
Let mid point of AB,BC,CD,DA are P,Q,R,S respectively.
To prove:- PQRS is a parallelogram.
Draw diagonal BD and PS is mid segment of ΔABD therefore PS∣∣BD also QR is mid segment ΔBCD therefore QR∣∣BD
∵PS∣∣BD and QR∣∣BD
∴PS∣∣QR
Draw diagonal AC,SR is the mid segment of ΔACD therefore SR∣∣AC also PQ is the mid segment of ΔABC therefore PQ∣∣AC
∵SR∣∣AC and PQ∣∣AC
∴SR∣∣PQ
∵PS∣∣QR and SR∣∣PQ
∴ quadrilateral PQRS is a parallelogram as. A parallelogram is a simple quadritiral with two pairs of parallel sides.
Q18: State the angle sum property of a quadrilateral.
Ans: The sum of angles of a quadrilateral is 360°. This is the angle sum property of quadrilaterals.
Q19: ABCD is a parallelogram. The circle through A,B and C intersects CD produced at E. If AB=10 cm,BC=8 cm,CE=14 cm . Find AE
Ans: Given : ABCD is a parallelogram and a circle is drawn through A,B and C which intersects CD produced, at E
AB=10cm BC=8cm CE=14cm
Now,
∠AED+∠ABC=180º →(1) (Sum of opposite angles of a cyclic quadrilateral is supplementary)
∠EDA+∠ADC=180º →(2) (linear pair)
∠EDA+∠ABC=18º →(3) (∵ ∠ADC=∠ABC as they are the opposite angles of a parallelogram)
From (1) & (3) we have, ∠AED=∠EDA→(4)
⇒ in ΔAED two angles are equal, hence the opposite sides corresponding to these angles must also be equal
i.e. AE=AD
and AD=BC (opposite sides of a parallelogram are equal)
∴ AE=8cm.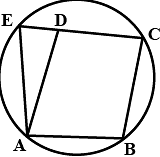
Q20: If the tangents PA and PB from a point P to the circle with cetre O inclined to each other at the angle of 110 , then find ∠POA.
Ans: Given ∠BPA=110°
Since the angle subtended by the tangent at the boundary of circle is 90°
⇒∠A=∠B=90°
In PBAO
⇒∠P+∠B+∠O+∠A=360°
Sum of angles of a quadrilateral is 360°
⇒110°+90+90°+∠O=360°
⇒290+∠O=360°
⇒∠O=360°−290°
⇒∠AOB=70°
Hence, the answer is 70°.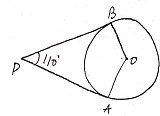
|
44 videos|412 docs|54 tests
|

|
Explore Courses for Class 9 exam
|

|

















