Class 9 Maths Chapter 11 Practice Question Answers - Surface Areas and Volumes
Q1: The dimensions of a cuboid in cm are 16 × 14 × 20. Find its total surface area.
Ans:
Total surface area of a cuboid =2(l × b + b × h + l × h)
Let A be the total surface area of the cuboid with length =16cm, breadth =14 cm and height =20 cm
Thus,
A = 2(16 × 14 + 14 × 20 + 20 × 16)
=2(224 + 280 + 320)
=1648cm2
Q2: The cuboid water tank has length 2 m, breadth 1.6m and height 1.8m. Find the capacity of the tank in litres.
Ans:
Volume of a cuboid of length l, breadth b and height h = l × b × h
So, the volume of the tank =2 × 1.6 × 1.8 = 5.76 m3
One m3 can occupy 1000 litres.
Hence, 5.76 m3 can occupy 5.76 × 1000=5760 litres.
Q3: What is the length of the sheet, 2 meter wide, required for making an open tank 15 m long, 10 m wide and 5 m deep?
Ans:
Area of the sheet required to make the tank
= lb + 2bh + 2lh
=15 × 10 + 2 × 10 × 6 + 2 × 15 × 6
=450m2
Length of the sheet required = Area / Width
= 450/2
m = 225m
Q4: How much length of the iron sheet 11 cm wide is required for making an open cylinder 15 cm high and 7 cm as base radius (π=22/7)?
Ans:
Surface of an open cylinder = area of the iron sheet
Let A be the surface area of open cylinder
A = πr2 + 2πrh
= 22/7 x 72 + 2 x 22/7 x 7 + 15
= (154+660)cm2
= 814cm2
Sheet is of the rectangular shape whose area is given as length times breadth.
∴ Length of the sheet
= (814 ÷ 11)cm
= 74cm
Q5: Is a square prism same as a cube? Explain.
Ans: Comparing a cube with a square prism
- A prism is a polyhedron whose base and top are congruent.
- A square prism has the base and top as equal square but its lateral faces need not be equal
- But a cube has base, top and lateral faces all congruent
- Hence, a square prism is not the same as a cube
Hence, A square prism is not a cube since its lateral faces need not be congruent to the base and top
Q6: 30 circular plates, each of radius 14 cm and thickness 3 cm are placed one above the another to form a cylindrical solid. Find the total surface area.
Ans:
Given, radius 14 cm, thickness =3 cm, number of plates = 30
Therefore, height of cylinder will be 3 × 30 = 90 cm
We know, total surface area of cylinder = 2πr(r + h) cm2
Therefore, total surface area =2π(14)(14 + (90)) = 9152 cm2
Q7: The total surface of a rectangular block is 846 cm2 . Find the volume, if the dimensions are in proportion 5 : 4 : 3.
Ans:
Let the dimensions be 5x, 4x, and 3x.
Total surface area =2(lb + bh + hl)
= 2(5x × 4x + 4x × 3x + 3x × 5x)cm2
= 94x2 cm2
Now,
94x2 = 846cm2 (given)
⇒ x2 = 9 or x = 3cm
∴ Volume of the block = 5x × 4x × 3x
= 60x3 = 1620cm3
Q8: A cone, a hemisphere and a cylinder stand on equal bases and have the same height What is the ratio of their respective volumes ?
Ans:
Let the volume of the cone, hemisphere, and cylinder be V1 ,V2 ,V3
Let the radius of the cone, hemisphere, and cylinder be r
∴ height of the hemisphere is also r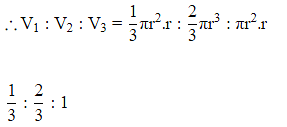
= 1 : 2 : 3
Q9: Rukhsar painted the outside of the cabinet of measure 1 m × 2m × 1.5 m . How much surface area did she cover if she painted all except the bottom of the cabinet?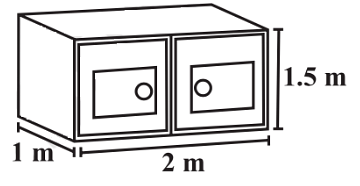 Ans:
Ans:
A cabinet has 6 surfaces including bottom surface.
However, we have to paint only 5 surfaces.
So, we have one front and one back surface (2 × 1.5), one left and one right surface (1 × 1.5) and one upper surface (2 × 1).
So, area to be painted is
= (2 × (2 × 1.5)) + (2 × (1 × 1.5)) + (2 × 1)
= 11 sq. m
Q10: The length, breadth and height of a room are 5 m, 4 m and 3 m respectively. Find the cost white washing the walls of the room and ceiling at the rate of Rs. 7.50 per m2.
Ans:
Given:
L= 5 m, B = 4 m, H = 3m
⇒ Area to be white-washed = Area of cuboid − Area of base.
=2lh + 2bh + 2lb − lb
=2lh + 2bh + lb
= [2 × 5 × 3 + 2 × 4 × 3 + 5 × 4]m2
= 74m2
Cost of white washing per m2 area = Rs.7.50
Cost of white washing 74m2 area = 74 × 7.50
= Rs.555
Q11: A road roller takes 750 complete revolutions to move once over to level a road. Find the area of the road if the diameter of a road roller is 84 cm and length is 1 m. Ans:
Ans:
Given:
⇒ D = 84 cm, l = 1m
⇒ r = 42cm
⇒ Area of road covered in 1 revolution = 2πrl = 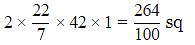 m
m
⇒ Area of road covered in 750 revolution = 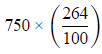
= 1980 sq m
Q12: The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of 10 per m2 is 15000, find the height of the hall (in meters).
Ans:
Given:
Perimeter = 250m
⇒ Area of 4 walls = 2lh + 2bh
= 2(b + l)h
⇒ Perimeter of floor of wall = 2l + 2b
⇒ 2(l + b) = 250 m
∴ Area of 4 walls =2(l + b)h
= 250h m2
⇒Cost of painting per m2 area = Rs. 10
⇒ Cost of painting 250h m2 area = Rs(250h × 10)
= Rs.2500h
⇒ Painting cost of walls = Rs. 15000
⇒ 2500h = 15000
⇒ h = 15000/2500
⇒ h= 6m
Q13: A small indoor greenhouse (herbarium) is made entirely of glass panes (including base) held together with tape. It is 30 cm long, 25 cm wide and 25 cm high.
(i) What is the area of the glass?
(ii) How much of tape is needed for all the 12 edges?
Ans:
Given:
⇒ l = 30, b = 25, h = 25
(i) Total S.A of green house
=2(lb+bh+lb)
= 2(30 × 25 + 30 × 25 + 25 × 25)
= 4250 cm2
(ii) For 12 edges: Total length
= 4l + 4b + 4h
= 4(30 + 25 + 25)
= 320 cm
Q14: Find the side of a cube whose surface area is 600 sq. cm
Ans:
Surface area = 600 sq.cm
⇒ 6l2 = 600 ...... where l is side of cube.
⇒ l = 10 cm
Side of cube = 10 cm
Q15: From a solid wooden cube of sides 14 cm a biggest hemispherical depression is carved out. What is the total surface area of the remain solid?
Ans:
Total surface area of remaining solid
= 6a2 −πr2 +2πr2
= 6a2 +πr2
= 6(14)2 + 22/7 x 7 x 7
= 6 x 196 + 154
= 1330 cm2
Q16: A box with a lid is made of wood which is 3 cm thick. Its external length, breadth and height are 5 cm,39 cm and 30 cm respectively. Find the capacity of the box. Also find the volume of wood used to make the box.
Ans:
Volume = (56 − 6) × (39 − 6) × (30 − 6)
= 39600cm3
Volume of wood =3cm×SAofexternalbox
⇒3 × 2(56 × 39 + 56 × 30 × 39 × 30)
⇒ 30204cm3 .
Hence, the answer is 30204cm3 .
Q17: Mary wants to decorate her Christmas tree. She wants to place the tree on a wooden block covered with colored paper with a picture of Santa Claus on it. She must know the exact quantity of paper to buy for this purpose. If the box has length, breadth and height as 80cm,40cm and 20cm respectively. How many square sheets of paper of side 40cm would she require?
Ans:
Quantity of paper required by Mary to cover the wooden block is equal to its total surface area which is equal to
2(80 × 40 + 40 × 20 + 20 × 80)cm2 = 11200 cm2
Number of square sheets of paper of side 40cm = 11200 / 40 x 40 = 7
Q18: Find the volume of a sphere whose radius is 7 cm.
Ans:
Given, radius of the sphere =7 cm
We know that the volume of sphere with radius r is V = 4/3πr3.
Thus,
Volume = 4/3πr3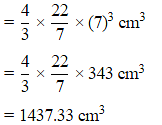
Hence, the volume of the sphere is 1437.33 cm3
Q19: The three coterminous edges of a rectangular solid are 36 cm, 75 cm and 80 cm respectively, find the edge of a cube which will be of the same capacity.
Ans:
Let the edge of the cube having same capacity be a.
Volume of the cube = Volume of the cuboid
(a)3 = 36 × 75 × 80
= (3 × 3 × 4 × 5 × 5 × 3 × 4 × 4 × 5)
= (3 × 4 × 5)3
a = (3 × 4 × 5)
= 60 cm
Q20: Two cubes each of edge 12 cm are joined end to end. Find the surface area of the resulting cuboid.
Ans:
Length of the resulting cuboid\
= (12 + 12)cm
= 24cm
Breadth and height remaining the same i.e. 12 cm each
Surface area = 2(lb + bh + lh)
= 2(24 × 12 + 12×12 + 24 × 12)2
= 1440cm2
|
44 videos|412 docs|54 tests
|
























