Class 10 Maths Chapter 2 Case Based Questions - Polynomials
| Table of contents |

|
| Case Study – 1 |

|
| Case Study – 2 |

|
| Case Study – 3 |

|
| Case Study – 4 |

|
| Case Study – 5 |

|
Case Study – 1
Basketball and soccer are played with a spherical ball. Even though an athlete dribbles the ball in both sports, a basketball player uses his hands and a soccer player uses his feet. Usually, soccer is played outdoors on a large field and basketball is played indoor on a court made out of wood. The projectile (path traced) of soccer ball and basketball are in the form of parabola representing quadratic polynomial.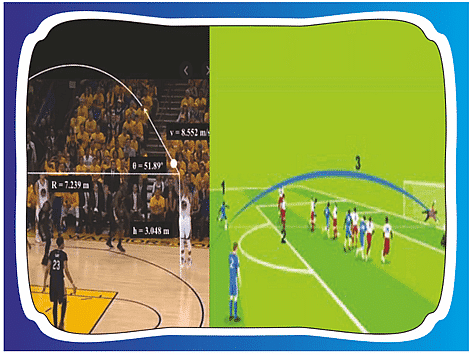 Q1: The shape of the path traced shown is
Q1: The shape of the path traced shown is
(a) Spiral
(b) Ellipse
(c) Linear
(d) Parabola
Ans: (d)
Explanation: The pose shown above are in the format of parabola. Hence, the correct option is (D).
Q2: The graph of parabola opens upwards, if
(a) a = 0
(b) a < 0
(c) a > 0
(d) a ≥ 0
Ans: (c)
Explanation: If a > 0, the parabola is upward. If a < 0, the parabola is downward. Hence, the correct option is (C).
Case Study – 2
An asana is a body posture, originally and still a general term for a sitting meditation pose, and later extended in hatha yoga and modern yoga as exercise, to any type of pose or position, adding reclining, standing, inverted, twisting, and balancing poses. In the figure, one can observe that poses can be related to representation of quadratic polynomial.

Q1: The shape of the poses shown is
(a) Spiral
(b) Ellipse
(c) Linear
(d) Parabola
Ans: (d)
Explanation: The pose shown above are in the format of parabola. Hence, the correct option is (D).
Q2: The graph of parabola opens downwards, if
(a) a ≥ 0
(b) a = 0
(c) a < 0
(d) a > 0
Ans: (c)
Explanation: If a > 0, the parabola is upward. If a < 0, the parabola is downward. Hence, the correct option is (C).
Q3: The zeroes of the quadratic polynomial 4√3 x² + 5x – 2√3 are
(a) 2/√3, √3/4
(b) -2/√3, √3/4
(c) 2/√3, -√3/4
(d) -2/√3, -√3/4
Ans: (b)
Explanation: The step-by-step process to solve the problem is as follows:
Step 1: Given the quadratic polynomial is 4√3x² + 5x – 2√3.
Step 2: We can rewrite the middle term (5x) by splitting it into two terms such that the sum of the two terms is 5x and their product is equal to the product of the first term (4√3x²) and the last term (-2√3). So, 5x can be written as 8x - 3x.
Step 3: Now, rewrite the polynomial: 4√3x² + 8x - 3x - 2√3.
Step 4: Take out the common factors from the first two terms and the last two terms separately. From the first two terms, the common factor is 4x, and from the last two terms, the common factor is -√3. So we get: 4x(√3x + 2) - √3(√3x + 2).
Step 5: Again, take out the common factor from the two terms, which is (√3x + 2). We then get: (√3x + 2)(4x - √3).
Step 6: Equate the quadratic polynomial to zero and solve for x to find the roots of the polynomial. If (√3x + 2)(4x - √3) = 0, then either √3x + 2 = 0 or 4x - √3 = 0.
Step 7: Solving √3x + 2 = 0 gives x = -2/√3 and solving 4x - √3 = 0 gives x = √3/4.
Therefore, the zeroes of the given quadratic polynomial are -2/√3 and √3/4. Hence, the correct option is (b) -2/√3, √3/4.
Case Study – 3
Observe the position of the athlete taking long jump. He use to follow every time a particular shape of path. In the figure, a student can observe that the different positions can be related to representation of quadratic polynomial.
Q1: The path of the different positions form a
(a) Spiral
(b) Ellipse
(c) Linear
(d) Parabola
Ans: (d)
Explanation: When we draw a dotted line following the different positions of athlete, it show a parabolic path. So, it is a parabola. Hence, the correct option is (D).
Q2: If the above case is represented by quadratic polynomial ax² + bx + c, then
(a) a ≥ 0
(b) a = 0
(c) a < 0
(d) a > 0
Ans: Option C
Explanation: If a > 0, the parabola is upward. If a < 0, the parabola is downward. Hence, the correct option is (C).
Q3: If the sum of zeros of quadratic polynomial ax² + bx + c is equal to product of zero, then
(a) b + c = 0
(b) c + a = 0
(c) a + b = 0
(d) None of the above
Ans: (c)
Explanation: In the given question, it's stated that the sum of zeros of the quadratic polynomial ax² + bx + c is equal to the product of zero.
The general form of a quadratic polynomial is ax² + bx + c, where a, b, and c are constants. The sum and product of the zeros of the quadratic polynomial are given by the formulas:
Sum of zeros = -b/a
Product of zeros = c/a
According to the question, the sum of zeros is equal to the product of zeros. Therefore, we can equate the two equations:
-b/a = c/a
Cross multiplying, we get:
-b = c
But we know that c is the product of zeros and -b is the sum of zeros which cannot be equal unless a or b is zero. Therefore, we can conclude that a * b = 0.
So, our correct option is (C) a * b = 0.
Please note that this is only possible in exceptional cases where one or both of the zeros are zero, making the sum and product equal.
Case Study – 4
The below picture are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.

Q1: In the standard form of quadratic polynomial, ax² + bx + c, a, b and c are
(a) All are real numbers.
(b) All are rational numbers.
(c) ‘a’ is a non-zero real number and b and c are any real numbers.
(d) All are integers.
Ans: (c)
Explanation: Because if a = 0, the equation become linear. Then it is not a quadratic equation. Hence, the correct option is (C).
Q2: If the roots of the quadratic polynomial are equal, where the discriminant D = b² – 4ac, then
(a) D > 0
(b) D < 0
(c) D ≥ 0
(d) D = 0
Ans: (d)
Explanation: A quadratic polynomial is represented by the equation ax² + bx + c = 0, where a, b, and c are constants. The roots of a quadratic polynomial can be found using the quadratic formula, which is x = [−b ± sqrt(b² – 4ac)] / 2a. The term under the square root, b² – 4ac, is called the discriminant (D), and it determines the nature of the roots of the quadratic equation.
When the discriminant (D) is greater than 0 (D > 0), the quadratic equation has two distinct real roots. This happens when the parabola represented by the quadratic equation intersects the x-axis at two distinct points.
When the discriminant (D) is less than 0 (D < 0), the quadratic equation has no real roots. This happens when the parabola represented by the quadratic equation does not intersect the x-axis at any point.
Finally, when the discriminant (D) is equal to 0 (D = 0), the quadratic equation has exactly one real root. This happens when the parabola represented by the quadratic equation just touches the x-axis at a single point. In other words, the parabola has a vertex on the x-axis.
Given that the roots of the quadratic polynomial in the question are equal, this means that the discriminant should be equal to 0 (D = 0). Hence, the correct option is (d) D = 0.
Q3: If α and 1/ α are the zeroes of the quadratic polynomial 2x² – x + 8k, then k is
(a) 4
(b) 1/4
(c) -1/4
(d) 2
Ans: (b)
Explanation: The problem is related to the properties of the roots of a quadratic polynomial. A quadratic polynomial is of the form ax² + bx + c, where a, b, and c are constants and a ≠ 0. The roots of a quadratic polynomial are given by the formula x = [-b ± sqrt(b² - 4ac)] / 2a.
Here, the quadratic polynomial is given as 2x² – x - 8k. Comparing it with the general form of a quadratic polynomial, we can see that a = 2, b = -1, and c = -8k.
We are given that the roots of the polynomial are α and 1/α. The product of the roots of a quadratic polynomial is given by c/a. Therefore, the product of the roots α and 1/α is -8k / 2 = -4k.
According to the problem, α x (1/α) = -4k. Since any number multiplied by its reciprocal is 1, this simplifies to 1 = -4k.
Solving for k, we get k = 1 / -4 = -1/4.
Therefore, the correct answer is (c) -1/4. The answer given as (b) 1/4 appears to be a mistake.
Q4: The graph of x² + 1 = 0
(a) Intersects x‐axis at two distinct points.
(b) Touches x‐axis at a point.
(c) Neither touches nor intersects x‐axis.
(d) Either touches or intersects x‐ axis.
Ans: (c)
Explanation: The given equation: x² + 1 = 0 or 1.x² + 0.x + 1 = 0 Here, a = 1, b = 0 and c = 1 D = b² – 4ac = 0² – 4 х 1 х 1 = – 4, therefore, there is no real root. So, the graph of the equation neither touches nor intersects x‐axis. Hence, the correct option is (C).
Q5: If the sum of the roots is –p and product of the roots is -1/p, then the quadratic polynomial is
(a) k(-px² + x/p + 1)
(b) k(px² – x/p – 1)
(c) k(x² + px – 1/p)
(d) k(x² – px + 1/p)
Ans: (c)
Explanation: To solve this problem, we need to understand the relationship between the roots of a quadratic equation and the coefficients of the equation itself. The general form of a quadratic equation is k(ax² + bx + c), where k is a constant, and a, b, and c are the coefficients of the equation.
We know from the problem statement that the sum of the roots is -p and the product of the roots is -1/p. We also know from the properties of quadratic equations that the sum of the roots is equal to the negation of the coefficient of the x term (i.e., b) divided by the coefficient of the x² term (i.e., a), and the product of the roots is equal to the constant term (i.e., c) divided by the coefficient of the x² term (i.e., a).
So, if we let a = 1 (since the coefficient of x² is typically normalized to be 1), then we have b = -(-p) = p and c = -1/p.
Substituting these values into the general form of the equation, we get:
k(1*x² + p*x - 1/p) = k(x² + px - 1/p).
So, the correct option is (c), as the given equation matches this form.
Case Study – 5
During the skipping through skipping rope, its look like the in the form of parabola. It is a natural examples of parabolic shape which is represented by a quadratic polynomial. Similarly, we can observe in many other cases forming a in a variety of forms of different parabolas.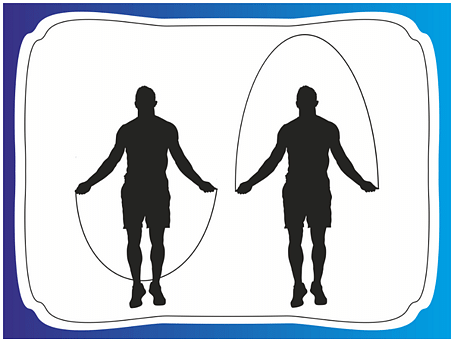
Q1: In the standard form of quadratic polynomial, ax² + bx + c, the condition between a, b and c are
(a) a may be 0, but b and c must be non-zero.
(b) a, b and c all may be zero.
(c) ‘a’ is a non-zero real number and b and c are any real numbers.
(d) All are integers.
Ans: (c)
Explanation: Because if a = 0, the equation become linear. Then it is not a quadratic polynomial. Hence, the correct option is (C).
Q2: If the roots of the quadratic polynomial are unequal, where the discriminant D = b² – 4ac, then
(a) D > 0
(b) D < 0
(c) D ≥ 0
(d) D = 0
Ans: (a)
Explanation: A quadratic polynomial can be written in the form of ax² + bx + c = 0, where a, b, and c are constants, and a ≠ 0. The roots of this equation are given by the quadratic formula:
x = [-b ± sqrt(b² - 4ac)] / 2a
The term within the square root, b² - 4ac, is called the discriminant (D). The value of the discriminant determines the nature of the roots of the quadratic polynomial.
1. If D > 0, then the roots are real and unequal. This is because we're taking the square root of a positive number, which leads to two different roots due to the ± sign in the quadratic formula.
2. If D = 0, then the roots are real and equal. This is because the square root of zero is zero, and the ± sign no longer results in different roots.
3. If D < 0, then the roots are complex or imaginary. This is because the square root of a negative number is not a real number, leading to imaginary roots.
So, if the roots of the quadratic polynomial are unequal, it means that the discriminant (D) must be greater than 0. This is why the correct answer is (a) D > 0.
Q3: If α and -α are the zeroes of the quadratic polynomial 2x² – 3(k – 4)x – 8, then k is
(a) 4
(b) 1/4
(c) -1/4
(d) 2
Ans: (a)
Explanation: The given quadratic polynomial is 2x² – 3(k – 4)x – 8. The roots of the polynomial are α and -α.
In a quadratic equation of the form ax² + bx + c = 0, the sum of the roots is given by -b/a and the product of the roots is given by c/a.
Here, the sum of the roots α and -α is equal to -(-3(k – 4))/2 = 3(k – 4)/2. This is because the coefficient of x in the polynomial is -3(k – 4) and the coefficient of x² is 2.
Now, since the roots are α and -α, their sum is α - α = 0.
Therefore, equating the sum of the roots to zero, we have 3(k – 4)/2 = 0. Simplifying this equation gives us k – 4 = 0.
Solving further, we find the value of k to be 4.
Therefore, the answer is (a) 4.
Q4: The graph of x² – 1 = 0
(a) Intersects x‐axis at two distinct points.
(b) Touches x‐axis at a point.
(c) Neither touches nor intersects x‐axis.
(d) Either touches or intersects x‐ axis at one point.
Ans: (a)
Explanation: The given equation: x² – 1 = 0 or 1.x² + 0.x – 1 = 0 Here, a = 1, b = 0 and c = – 1 D = b² – 4ac = 0² – 4 х 1 х(- 1) = 4, therefore, there is two real root. So, the graph of the equation intersects x‐axis at two distinct points. Hence, the correct option is (A).
Q5: If the sum of the roots is p and product of the roots is -p, then the quadratic polynomial is
(a) k(px² + p + P)
(b) k(px² – x/p – 1)
(c) k(x² – px – p)
(d) k(x² – px + p)
Ans: (c)
Explanation: The question is based on the concept of roots of a quadratic polynomial. In a quadratic polynomial represented by ax² + bx + c = 0, the sum of the roots is given by -b/a and the product of the roots is given by c/a.
In this question, we are given that the sum of the roots is p and the product of the roots is -p. So, we can replace -b/a with p and c/a with -p.
Now, we can write the quadratic polynomial in the form of k [x² – (sum of roots)x + product of roots]. The value of sum of roots is p and the product of the roots is -p. Substituting these values, we get k [x² – (p)x - p].
So, the quadratic polynomial is k(x² – px – p), which is option (c).
In other words, a quadratic polynomial is generally represented as k(x² – Sx + P), where S is the sum of roots and P is the product of roots. In this case, S = p and P = -p. By substituting these values, we arrive at the quadratic polynomial k(x² – px – p), which is option (c).

|
Explore Courses for Class 10 exam
|

|

















