Class 10 Maths Chapter 3 Case Based Questions - Pair of Linear Equations in Two Variables

Case study - 1

It is common that Governments revise travel fares from time to time based on various factors such as inflation ( a general increase in prices and fall in the purchasing value of money) on different types of vehicles like auto, Rickshaws, taxis, Radio cab etc. The auto charges in a city comprise of a fixed charge together with the charge for the distance covered. Study the following situations:
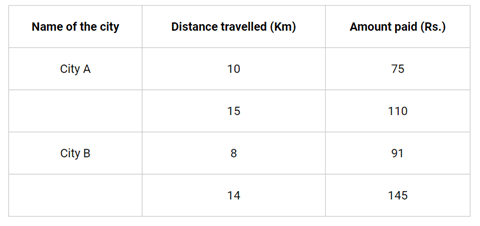Situation 1: In city A, for a journey of 10 km, the charge paid is Rs 75 and for a journey of 15 km, the charge paid is Rs 110.
Situation 2: In a city B, for a journey of 8km, the charge paid is Rs91 and for a journey of 14km, the charge paid is Rs 145.

Refer situation 1:
Q1: If the fixed charges of auto rickshaw be Rs x and the running charges be Rs y km/hr, the pair of linear equations representing the situation is
(a) x + 10y =110, x + 15y = 75
(b) x + 10y = 75, x + 15y = 110
(c) 10x + y = 110, 15x + y = 75
(d) 10x + y = 75, 15x + y = 110
Ans: (b)
Explanation: The cost of the auto rickshaw ride consists of two components - a fixed charge (x) and a variable charge based on the distance of the journey (y per km). The total cost of the ride would therefore be the sum of these two components.
In the first situation, the auto rickshaw ride in city A costs Rs 75 for a 10 km journey and Rs 110 for a 15 km journey. We can express these two situations as two linear equations:
For the 10 km journey: x + 10y = 75 (equation 1)
For the 15 km journey: x + 15y = 110 (equation 2)
Where x is the fixed charge and y is the cost per km.
Therefore, the pair of linear equations representing the situation is x + 10y = 75, x + 15y = 110 (option b). 

Q2: A person travels a distance of 50km. The amount he has to pay is
(a) Rs.155
(b) Rs.255
(c) Rs.355
(d) Rs.455
Ans: (c)
Explanation: To solve this case-based problem, we first need to understand the relationship between distance traveled and the charge paid. This can be represented as a linear equation in the form of y = mx + c, where y is the charge paid, m is the rate charged per km, x is the distance traveled, and c is the fixed charge.
From Situation 1, we have two equations based on the given data:
1) 75 = 10m + c
2) 110 = 15m + c
Subtracting equation 1 from equation 2, we get:
35 = 5m
So, m = 35/5 = 7. This means the rate charged per km in city A is Rs. 7.
Substituting m = 7 in equation 1, we get:
75 = 10*7 + c
So, c = 75 - 70 = 5. This means the fixed charge in city A is Rs. 5.
So, the total charge for traveling a distance of x km in city A is given by the equation:
Charge = 7x + 5
Now, let's calculate the charge for traveling a distance of 50km in city A:
Charge = 7*50 + 5 = Rs. 355
Therefore, the answer is (c) Rs. 355. 

Refer situation 2:
Q3: What will a person have to pay for travelling a distance of 30km?
(a) Rs.185
(b) Rs.289
(c) Rs.275
(d) Rs.305
Ans: (b)
Explanation: To solve this problem, we first need to find the rate of the fare per kilometer and the fixed charge in city B. We can solve this problem by making two equations from the given situations and then solve them simultaneously.
Let's take the fixed charge as F (in Rs.) and the rate per kilometer as R (in Rs. per km).
From the given situation 2, we know that:
For a journey of 8km, the charge paid is Rs 91.
For a journey of 14km, the charge paid is Rs 145.
So, we can formulate two equations:
1) F + 8R = 91
2) F + 14R = 145
Subtract equation 1 from equation 2 and we get 6R = 54, therefore R = 54/6 = 9 Rs per km.
Substitute the value of R in equation 1, we get F = 91 - 8*9 = 91 - 72 = 19 Rs.
So, the fixed charge is Rs 19 and the fare per kilometer is Rs 9 in city B.
Now, to find out what a person will have to pay for traveling a distance of 30km, we add the fixed charge to the product of the fare per kilometer and the distance.
Therefore, the fare for 30km = F + 30R = 19 + 30*9 = 19 + 270 = Rs 289.
So, the correct answer is (b) Rs.289. 

Case Study - 2

Amit is planning to buy a house and the layout is given below. The design and the measurement has been made such that areas of two bedrooms and kitchen together is 95 sq.m.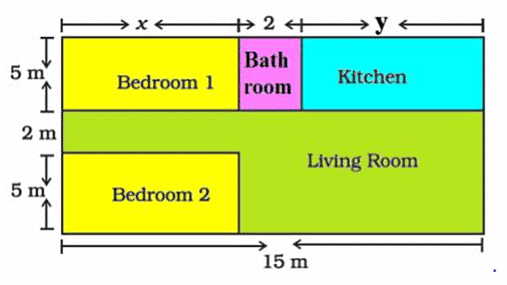

Based on the above information, answer the following questions:
Q1: Form the pair of linear equations in two variables from this situation.
Ans: Area of two bedrooms= 10x sq.m
Area of kitchen = 5y sq.m
10x + 5y = 95
2x + y =19
Also, x + 2+ y = 15
x + y = 13

Q2: Find the length of the outer boundary of the layout.
Ans: Length of outer boundary = 12 + 15 + 12 + 15 = 54m 

Q3: Find the area of each bedroom and kitchen in the layout.
Ans: On solving two equation part(i)
x = 6m and y = 7m
area of bedroom = 5 x 6 = 30m
area of kitchen = 5 x 7 = 35m

Q4: Find the area of living room in the layout.
Ans: Area of living room = (15 x 7) – 30 = 105 – 30 = 75 sq.m 

Q5: Find the cost of laying tiles in kitchen at the rate of Rs. 50 per sq.m.
Ans: Total cost of laying tiles in the kitchen = Rs.50 x 35 = Rs1750.

Case Study - 3

A test consists of ‘True’ or ‘False’ questions. One mark is awarded for every correct answer while ¼ mark is deducted for every wrong answer. A student knew answers to some of the questions. Rest of the questions he attempted by guessing. He answered 120 questions and got 90 marks.

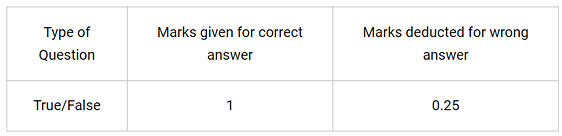Q1: If answer to all questions he attempted by guessing were wrong, then how many questions did he answer correctly?
Ans: Let the no of questions whose answer is known to the student x and questions attempted by cheating be y
x + y =120
x – 1/4y =90
solving these two
x = 96 and y = 24
He answered 96 questions correctly. 

Q2: How many questions did he guess?
Ans: Let the no of questions whose answer is known to the student x and questions attempted by cheating be y
x + y =120
x – 1/4y =90
solving these two
x = 96 and y = 24
He attempted 24 questions by guessing. 

Q3: If answer to all questions he attempted by guessing were wrong and answered 80 correctly, then how many marks he got?
Ans: Let the no of questions whose answer is known to the student x and questions attempted by cheating be y
x + y =120
x – 1/4y =90
solving these two
x = 96 and y = 24
Marks = 80- ¼ 0f 40 =70

Q4: If answer to all questions he attempted by guessing were wrong, then how many questions answered correctly to score 95 marks?
Ans: Let the no of questions whose answer is known to the student x and questions attempted by cheating be y
x + y =120
x – 1/4y =90
solving these two
x = 96 and y = 24
x – 1/4 of (120 – x) = 95
5x = 500, x = 100