Class 10 Maths Chapter 9 Practice Question Answers - Some Applications of Trigonometry
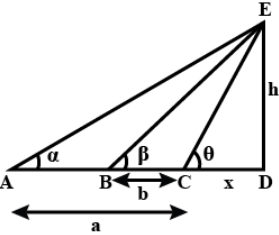
Q1: Two stations due South of a leaning tower which leans towards the North, are at distances a and b from its foot. If α and β are the elevations of the top of the tower from these stations, then prove that its inclination θ to the horizontal is given by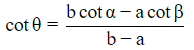
Ans: height of the tower DE = h
Distance between first station to foot of tower AD = a + x
Distance between second station to foot of tower BD = b + x
Distance between C and D = x
Give α, β are the angle of elevation two stations to top of the tower
thatis ∠DAE = α, ∠DBE = β, ∠DCE = θ
In Δ ADE
Cot θ = x/h _______(1)
In Δ BDE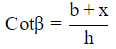
(b + x) = h Cotβ (multiply an on both sides )
(ab + ax) = haCot β ________(2)
In Δ CDE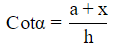
(a + x) = hCotα (multiply b on both sides )
(ab + bx) = hbCotα _______ (3)
substract(3)−(2)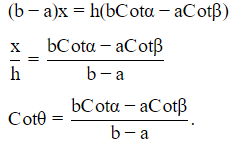
Q2: There are two towers one on each bank of a river, just opposite to each other one tower is 50m high. From the top of this tower, the angles of depression of the top and foot of the other tower are 30o and 60o respectively. Find the width of the river and the height of the other tower.
Ans: Let AB and CE are two temples each at the bank of river. The top of the temple CE makes angle of depressions at the top and bottom of tower AB are 30° and 60° Let CE = 50m and AB = H m and ∠CBE = 60, ∠DAE = 30 The corresponding figure is as follows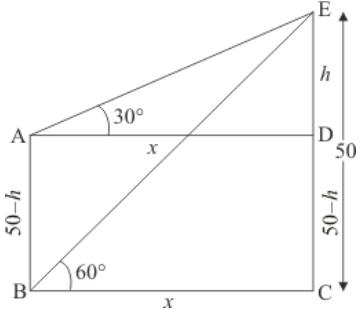
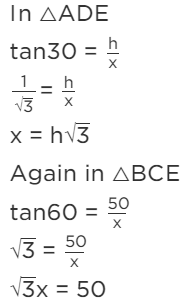
h = 50/3
Now the distance between the temples,
Therefore, H = 50 − h = 50 − 50/3 = 33.33 m.
Hence distance between the temples is 28.83m and height of temple is 33.33m.
Q3: The angles of depression of the top and bottom of a building 50 meters high as 4 observed from the top of a tower are 30 and 60, respectively. Find the height of the tower and also the horizontal distance between the building and the tower.
Ans: In ΔBTP,
tan 30° = TP/BP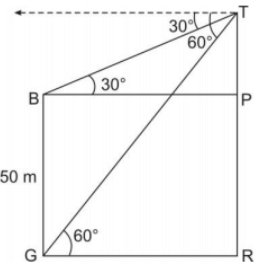 1/√3 = TP/BP
1/√3 = TP/BP
BP = TP√3
In ΔGTR,
tan 60° = TR/GR
√3 = TR/GR
GR = TR/√3
As BP = GR
TP√3 = TR/√3
3 TP = TP + PR
2 TP = BG
TP = 50/2 m = 25 m
Now, TR = TP + PR
TR = (25 + 50) m
Height of tower = TR = 75 m
Distance between building and tower = GR = TR/√3
GR = 75/√3 m = 25√3 m
Q4: From the top of a 70m tall tower, the angle of depression of the top and the base of a pole are found to be 30 and 45 respectively. Find the distance of the pole from the tower and the height of the pole.
Ans: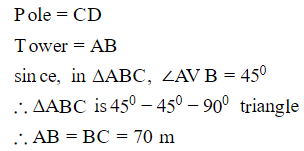
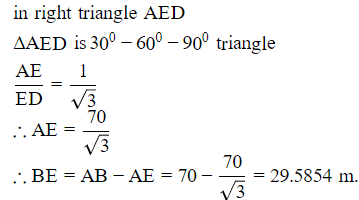
Q5: At the foot of a mountain, the elevation of its summit is 45∘ , after ascending 2 km towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘. Find the height of the mountain.
Ans: Let A be the foot and B be the summit of the mountain OB at height h.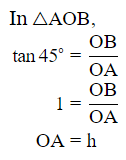
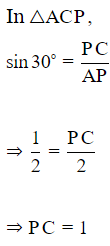
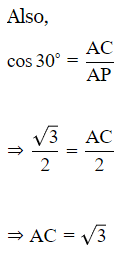
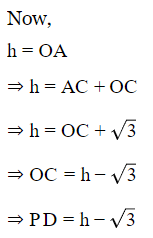

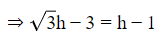
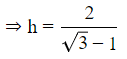
⇒ h = √3 +1
⇒ h ≈ 2.732 km
Hence, the height of the mountain is 2.732 km.

|
Explore Courses for Class 10 exam
|

|
















