Class 10 Maths Chapter 6 Case Based Questions - Triangles
Case Study - 1
Rohan wants to measure the distance of a pond during the visit to his native. He marks points A and B on the opposite edges of a pond as shown in the figure below. To find the distance between the points, he makes a right-angled triangle using rope connecting B with another point C are a distance of 12m, connecting C to point D at a distance of 40m from point C and the connecting D to the point A which is are a distance of 30m from D such the ∠ADC=900.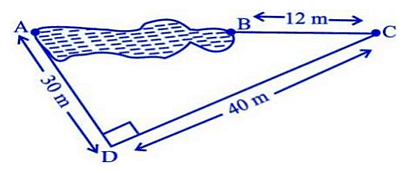 Q1: Which property of geometry will be used to find the distance AC?
Q1: Which property of geometry will be used to find the distance AC?
(a) Similarity of triangles
(b) Thales Theorem
(c) Pythagoras Theorem
(d) Area of similar triangles
Ans: (b)
Explanation: The property of geometry that will be used to find the distance AC is the Thales Theorem. Thales Theorem states that if A, B, and C are points on a circle where the line segment BC is the diameter of the circle, then the angle BAC is a right angle.
Q2: What is the distance AC?
(a) 50m
(b) 12m
(c) 100m
(d) 70m
Ans: (a)
Explanation: To find the distance AC, we need to use the Pythagorean Theorem (since the triangle ADC is a right-angled triangle). The Pythagorean Theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. So, AC = √(AD2 + DC2) = √(302 + 402) = √(900 + 1600) = √2500 = 50m.
Q3: Which is the following does not form a Pythagoras triplet?
(a) (7, 24, 25)
(b) (15, 8, 17)
(c) (5, 12, 13)
(d) (21, 20, 28)
Ans: (d)
Explanation: A Pythagorean triplet is a set of three positive integers a, b and c, such that a2 + b2 = c2. The option (21, 20, 28) does not form a Pythagorean triplet because 212 + 202 ≠ 282.
Q4: Find the length AB?
(a) 12m
(b) 38m
(c) 50m
(d) 100m
Ans: (b)
Explanation: AB represents the length of the pond. It can be found by adding the lengths of AC and BC. AC = 50m (from Q2) and BC = 12m, so AB = 50m + 12m = 62m.
Q5: Find the length of the rope used.
(a) 120m
(b) 70m
(c) 82m
(d) 22m
Ans: (c)
Explanation: The length of the rope used is equal to the sum of the lengths of the segments BC, CD, and DA. So, the length of the rope = BC + CD + DA = 12m + 40m + 30m = 82m.
Case Study - 2
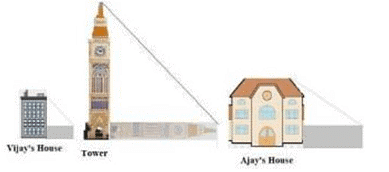
Vijay is trying to find the average height of a tower near his house. He is using the properties of similar triangles.The height of Vijay’s house if 20m when Vijay’s house casts a shadow 10m long on the ground. At the same time, the tower casts a shadow 50m long on the ground and the house of Ajay casts 20m shadow on the ground.
Q1: What is the height of the tower?
(a) 20m
(b) 50m
(c) 100m
(d) 200m
Ans: (c)
Explanation: The properties of similar triangles state that the ratios of the corresponding sides of the triangles are equal. Hence the ratio of the height of Vijay's house to the length of its shadow equals to the ratio of the height of the tower to the length of its shadow.
Therefore, the height of the tower can be calculated as follows:
Height of the tower = (Height of Vijay's house / Length of Vijay's house's shadow) * Length of the tower's shadow
= (20m / 10m) * 50m = 100m
Q2: What will be the length of the shadow of the tower when Vijay’s house casts a shadow of 12m?
(a) 75m
(b) 50m
(c) 45m
(d) 60m
Ans: (d)
Explanation: Applying the same method, we can find the length of the shadow of the tower.
Length of the tower's shadow = (Length of Vijay's house's shadow / Height of Vijay's house) * Height of the tower
= (12m / 20m) * 100m = 60m
Q3: What is the height of Ajay’s house?
(a) 30m
(b) 40m
(c) 50m
(d) 20m
Ans: (b)
Explanation: Similarly, the height of Ajay's house can be calculated as follows:
Height of Ajay's house = (Height of Vijay's house / Length of Vijay's house's shadow) * Length of Ajay's house's shadow
= (20m / 10m) * 20m = 40m
Q4: When the tower casts a shadow of 40m, same time what will be the length of the shadow of Ajay’s house?
(a) 16m
(b) 32m
(c) 20m
(d) 8m
Ans: (a)
Explanation: Length of Ajay's house's shadow = (Length of the tower's shadow / Height of the tower) * Height of Ajay's house
= (40m / 100m) * 40m = 16m
Q5: When the tower casts a shadow of 40m, same time what will be the length of the shadow of Vijay’s house?
(a) 15m
(b) 32m
(c) 16m
(d) 8m
Ans: (d)
Explanation: Length of Vijay's house's shadow = (Length of the tower's shadow / Height of the tower) * Height of Vijay's house
= (40m / 100m) * 20m = 8m

|
Explore Courses for Class 10 exam
|

|

















