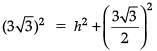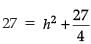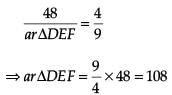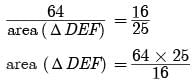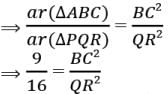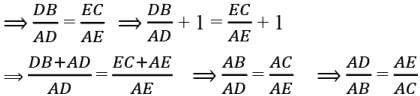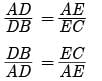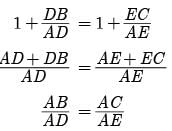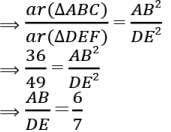Q1:
Question for Assertion & Reason Type Questions: Triangles
Try yourself:Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
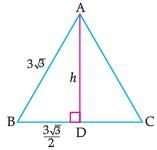
Assertion (A): In an equilateral triangle of side 3√3 cm, then the length of the altitude is 4.5 cm.
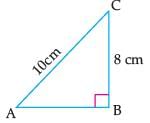
Reason (R): If a ladder 10 cm long reaches a window 8 m above the ground, then the distance of the foot of the ladder from the base of the wall is 6 m.
Explanation
In case of assertion

ΔABD, ∠D = 90°

or

or

or, h2 = 81/4
∴ h = 9/2 = 4.5 m
∴ Assertion is correct.
In case of reason: Let BC be the height of the window above the ground and AC be a ladder.

Here, BC = 8 cm and AC = 10 cm
∴ In right angled triangle ABC, AC2 = AB2 + BC2
(By using Pythagoras Theorem)
⇒ (10)2 = AB2 + (8)2
⇒ AB2 = 100 – 64
= 36
⇒ AB = 6 m.
∴ Reason is correct.
Hence, both assertion and reason are correct but reason is not the correct explanation for assertion.
Report a problem
Q2:
Question for Assertion & Reason Type Questions: Triangles
Try yourself: Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : In the ΔABC , AB = 24 cm , BC = 10 cm and AC = 26 cm , then ΔABC is a right angle triangle.
Reason : If in two triangles, their corresponding angles are equal, then the triangles are similar.
Explanation
We have, AB
2 + BC
2 = (24)
2 + (10)
2= 576 + 100 = 676 = 2
AB2 + BC2 = AC2
ABC is a right angled triangle.
Also, two triangle are similar if their corresponding angles are equal.
So, both A and R are correct but R does not explain A.
Report a problem
Q3:
Question for Assertion & Reason Type Questions: Triangles
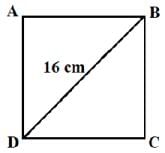
Try yourself: Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : The length of the side of a square whose diagonal is 16 cm, is 8√2 cm
Reason : In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Explanation
We know that In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. This is Pythagoras theorem. So, Reason is correct

Let the side of square be x cm.
In ∆ABD, by Pythagoras theorem, we have BD2 = AB2 + AD2
⇒ 162 = x2 + x2
⇒ 2x2 = 256 ⇒ x2 = 128 ⇒ x = 8√2 cm
So, Assertion is also correct.
Report a problem
Q4:
Question for Assertion & Reason Type Questions: Triangles
Try yourself: Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): Corresponding sides of two similar triangles are in the ratio of 2 : 3. If the area of the smaller triangle is 48 cm2, then the area of the larger triangle is 108 cm2.
Reason (R): If D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC, then CA2 = CB × CD.
Explanation
In case of assertion
Let ΔABC and ΔDEF are two similar triangles.

Given that ar ΔABC = 48 cm2. Then,

Thus, the area of larger triangle is 108 cm2.
∴ Assertion is correct.
In case of reason:

In ΔBAC and ΔADC,
∠BAC= ∠ADC [Given]
∠BCA= ∠ACD [Common angle]
By AA similarity, ΔBAC ~ ΔADC
Thus,
CA/CD = BC/CA
∴ Reason is correct.
Hence, both assertion and reason are correct but reason is not the correct explanation for assertion.
Report a problem
Q5:
Question for Assertion & Reason Type Questions: Triangles
Try yourself: Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : ABC and DEF are two similar triangles such that BC = 4 cm , EF = 5 cm and area of ΔABC = 64 cm2 , then area of ΔDEF = 100 cm2.
Reason : The areas of two similar triangles are in the ratio of the squares of teh corresponding altitudes.
Explanation
Reason is true. [standard result]
For Assertion, since ΔABC ∼ ΔDEF

(ratio of areas of two similar Δs is equal to the ratio of the squares of corresponding sides)

= 4 x 25 = 100 cm2
Assertion is true. But Reason is not correct explanation for Assertion.
Report a problem
Q6:
Question for Assertion & Reason Type Questions: Triangles
Try yourself: Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : The areas of two similar triangles ABC and PQR are in the ratio 9 :16. If BC = 4.5 cm, then the length of QR is 6 cm.
Reason : The ratio of the areas of two similar triangles is equal to the ratio of their corresponding sides.
Explanation
We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
So, Reason is not correct


So, Assertion is correct
Report a problem
Q7:
Question for Assertion & Reason Type Questions: Triangles
Try yourself: Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): If D is a point on side QR of ΔPQR such that PD ⊥ QR, then ΔPQD ~ ΔRPD.
Reason (R): In the figure given below, if ∠D = ∠C then ΔADE ~ ΔACB.

Explanation
In case of assertion

In ΔPQD and ΔRPD, ∠PDQ = ∠PDR= 90°.
There is no other information to be similar.
Thus, it is not it will be correct to say that ΔPQD ~ ΔRPD.
∴ Assertion is incorrect.
In case of reason:
In ΔADE and ΔACB, we have
∠ADE= ∠ACB [Given]
∠DAE= ∠CAB [Common angle]
By AA similarity, we get ΔADE ~ ΔACB.
∴ Reason is correct
Hence, assertion is incorrect but reason is correct
Report a problem
Q8:
Question for Assertion & Reason Type Questions: Triangles
Try yourself: Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : ABC is an isosceles, right triangle, right angled at C . Then AB2 = 3AC2
Reason : In an isosceles triangle ABC if AC = BC and AB2 = 2AC2 , then ∠C = 90°
Explanation
If Assertion is incorrect, but Reason is correct.
In right angled ΔABC ,

AB2 = AC2 + BC2(By Pythagoras Theorem)
= AC2 + AC2 [BC = AC]
= 2AC2AB2 = 2AC2
Assertion is false.
Again since, AB2 = 2AC2
= AC2 + AC2 = AC2 + BC2 (AC = BC given)
∠ = 90°
(By converse of Pythagoras Theorem)Reason is true.
Report a problem
Q9:
Question for Assertion & Reason Type Questions: Triangles
Try yourself: Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : In ∆ABC , AB = 6√3, AC = 12 cm and BC = 6cm then ∠B = 90°.
Reason : If in a triangle, square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
Explanation
We know that If in a triangle, square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle. This is converse of Pythagoras theorem.
So, Reason is correct
Now, AB2 = (6√3)2 = 108
AC2 = 122 = 144
and BC2 = 62 = 36
∴ 2 = 2 + 2
By converse of Pythagoras theorem, ∠B = 90°
So, Assertion is also correct.
Report a problem
Q10:
Question for Assertion & Reason Type Questions: Triangles
Try yourself: Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, then triangles will be similar.
Reason (R): If the ratio of the corresponding altitudes of two similar triangles is 3/5, then the
ratio of their areas is 6/5.
Explanation
In case of assertion: In the given two right triangles, both have equal right angles and one of the acute angles of one triangle is equal to an acute angle of the other triangle.
Thus, by AA similarity, the given two triangles are similar.
∴ Assertion is correct.
In case of reason:
We know that the ratio of the areas of two similar triangles is the square of the ratio of the corresponding altitudes of two similar triangles.
Thus, the ratio of the areas of two similar triangles is (3/5)2 = 9/25.
Report a problem
Q11:
Question for Assertion & Reason Type Questions: Triangles
Try yourself: Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : Two similar triangle are always congruent.
Reason : If the areas of two similar triangles are equal then the triangles are congruent.
Explanation
Two similar triangles are not congruent generally.
So, A is incorrect but R is correct.
Report a problem
Q12:
Question for Assertion & Reason Type Questions: Triangles
Try yourself: Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : ABC is an isosceles triangle right angled at C then AB2 = 2AC2.
Reason : If in a triangle, square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
Explanation
We know that If in a triangle, square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle. This is converse of Pythagoras theorem.
So, Reason is correct By
Pythagoras theorem, we have AB2 = AC2 + BC2
= AC2 + AC2 [∵ AC = BC Given]
⇒ AB2 = 2AC2So, Assertion is also correct.
But reason (R) is not the correct explanation of assertion (A).
Report a problem
Q13:
Question for Assertion & Reason Type Questions: Triangles
Try yourself: Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : ΔABC is an isosceles triangle right angled of C , then AB2 = 2AC2.
Reason : In right ΔABC , right angled at B, AC2 =AB2 +BC2.
Explanation
In an isosceles ΔABC , right angled at C is
AB2 = AC2 + BC2AB2 = AC2 + AC2AB2 = 2AC2 (AC = BC)
So, both A and R are correct and R explains A.
Report a problem
Q14:
Question for Assertion & Reason Type Questions: Triangles
Try yourself: Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : ABC is an isosceles triangle with AC = BC. If AB2 = 2 AC2, then ΔABC is a right triangle.
Reason : If in a triangle, square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
Explanation
We know that If in a triangle, square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle. This is converse of Pythagoras theorem.
So, Reason is correct
AB2 = 2AC2 = AC2 + AC2= BC2 + AC2 [∵ AC = BC Given]
⇒ AB2 = BC2 + AC2By converse of Pythagoras theorem, ΔABC is a right angled triangle.
So, Assertion is also correct.
Report a problem
Q15:
Question for Assertion & Reason Type Questions: Triangles
Try yourself:Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : ΔABC ~ ΔDEF such that ar(ΔABC) = 36cm2 and ar(ΔDEF) = 49cm2 then, AB : DE = 6 :7
Reason : If ΔABC ~ ΔDEF , then ar(ΔABC)/ar(ΔDEF) = AB2/DE2 = BC2/EF2 = AC2/DF2
Explanation
ar(ΔABC)/ar(ΔDEF) = AB2/DE2
36/49 = AB2/DE2
AB/DE = 6/7
AB:DE = 6:7
So, both A and R are correct and R explain A.
Report a problem
Q16:
Question for Assertion & Reason Type Questions: Triangles
Try yourself: Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : In the ∆ABC , AB = 24 cm, BC = 7 cm and AC = 25 cm, then ∆ABC is a right angle triangle.
Reason : The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Explanation
We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
So, Reason is correct
Now, AB2 + BC2 = 242 + 102
= 576 + 49 = 625
= AC2
⇒ AB2 + BC2 = AC2
By converse of Pythagoras theorem, ∆ABC is a right angled triangle.
So, Assertion is also correct.
But reason (R) is not the correct explanation of assertion (A).
Report a problem
Q17:
Question for Assertion & Reason Type Questions: Triangles
Try yourself: Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : In ∆ABC , DE|| BC such that AD = (7x - 4)cm, AE = (5 - 2)cm, DB = (3 + 4) cm and EC = 3 cm than x equal to 5.
Reason : If a line is drawn parallel to one side of a triangle to intersect the other two sides in distant point, than the other two sides are divided in the same ratio.
Explanation
We have,
AD/DB = AE/EC

21x2 - 12x = 15x2 + 20x - 6x - 8x
6x2 - 26x + 8 = 0
3x2 - 13x + 4 = 0
3x2 - 12x - x + 4 = 0
3x(x - 4) - 1(x - 4) = 0
(x - 4) (3x - 1) = 0

So, A is incorrect but R is correct.
Report a problem
Q18:
Question for Assertion & Reason Type Questions: Triangles
Try yourself: Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : If a line intersects sides AB and AC of a Δ ABC at D and E respectively and is parallel to BC, then AD/AB = AE/AC
Reason : If a line is parallel to one side of a triangle then it divides the other two sides in the same ratio.
Explanation
We know that If a line is parallel to one side of a triangle then it divides the other two sides in the same ratio. This is Basic Proportionality theorem.
So, Reason is correct.

By Basic Proportionality theorem, we have AD/DB = AE/EC

So, Assertion is correct
Report a problem
Q19:
Question for Assertion & Reason Type Questions: Triangles
Try yourself: Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : Assertion : If in a ∆ABC , a line DE || BC , intersects AB in D and AC in E , then AB/AD = AC/AE
Reason : If a line is drawn parallel to one side of a triangle intersecting the other two sides, then the other two sides are divided in the same ratio.
Explanation
Reason is true : [This is Thale’s Theorem]
For Assertion Since, DE || BC by Thale’s Theorem



Assertion (a) is true
Since, reason gives Assertion.
Report a problem
Q20:
Question for Assertion & Reason Type Questions: Triangles
Try yourself: Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : ΔABC ~ ΔDEF such that ar(ΔABC) = 36cm2 and ar(ΔDEF) = 49cm2. Then, the ratio of their corresponding sides is 6 : 7
Reason : The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Explanation
We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
So, Reason is correct

So, Assertion is correct.
Report a problem