Very Short Questions: Practical Geometry - Class 6 PDF Download

Q1: Draw ∆ABC. Draw perpendiculars from A, B and C respectively on the sides BC, CA and AB. Are there perpendicular concurrent? (passing through the same points).
Ans: Step I: Draw any ∆ABC.
Step II: Draw the perpendicular AD from A to BC.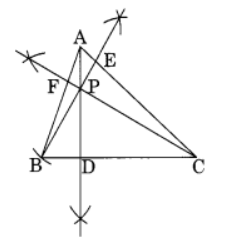
Step III: Draw the perpendicular BE from B to AC.
Step IV: Draw the perpendicular CF from C to AB.
We observe that the perpendiculars AD, BE and CF intersect each other at P.
Thus, P is the point of intersection of the three perpendiculars.

Q2: What is the first step in constructing a line segment of a given length?
Ans: The first step in constructing a line segment of a given length is to draw a line from the zero mark on the ruler to the mark that indicates the desired length.

Q3: How can you construct an angle of 60 degrees using a compass?
Ans: An angle of 60 degrees can be constructed by first drawing a line, putting the point of the compass at one end of the line, and drawing an arc. Then, without changing the compass width, put the point of the compass where the arc intersects the line and draw another arc intersecting the first arc. Draw a line from the point where the arcs intersect to the end of the original line.

Q4: What is a perpendicular bisector and how can you construct it?
Ans: A perpendicular bisector is a line that divides another line into two equal parts at a 90-degree angle. It can be constructed by drawing two arcs from the ends of the line segment that intersect above and below the line. Then draw a line through the points of intersection.

Q5: How can we construct a perpendicular bisector to a line segment?
Ans: We can construct a perpendicular bisector to a line segment using a compass and a straightedge or ruler. First, we draw two arcs from the ends of the line segment that intersect. Then, we draw a line through the point of intersection that will be perpendicular to the initial line segment and will bisect it. 

Q6: Using compasses and ruler, draw an angle of 75° and hence construct an angle of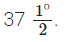
Ans: Step I: Draw a line segment OA.
Step II: Construct ∠BOA = 90° and ∠EOA = 60°
Step III: Draw OC as the bisector of ∠BOE, which equal to

Step IV: Draw the bisector OD of ∠COA.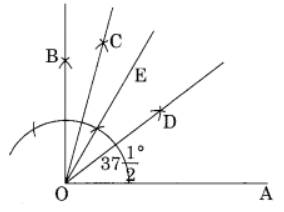
Thus ∠DOA is the required angle of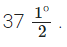

Q7: Draw an angle of 120° and hence construct an angle of 105°.
Ans: Step I: Draw a line segment
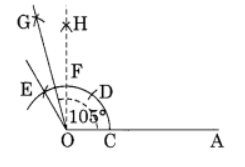Step II: With centre O and proper radius, draw an arc which meets OA at C.
Step III: With centre C and radius same, mark D and E on the previous arc.
Step IV: Join O to E and produce.
Step V: ∠EOA is the required angle of 120°.
Step VI: Construct an angle of 90° which meets the previous arc at F.
Step VII: With centre E and F and proper radius, draw two arcs which meet each other at G.
Step VIII: Join OG and produce.
Thus ∠GOA is the required angle of 105°.

Q8: Construct an angle of 60° and bisect it.
Ans: Step I: Draw a line segment

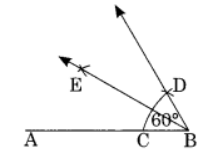
Step II: With centre B and proper radius, draw an arc which meets AB at C.
Step III: With C as centre and the same radius as in step II, draw an arc cutting the previous arc at D.
Step IV: Join B to D and produce.
Step V: Draw the bisector BE of ∠ABD.
Thus BE is the required bisector of ∠ABD.

Q9: Construct a perpendicular to a given line segment at point on it.
Ans: Step I: Draw a line  and take any point A on it.

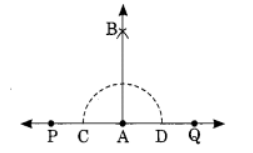
Step II: With centre A draw an arc which meets PQ at C and D.
Step III: Join AB and produce.
Step IV: With centres C and D and radius equal to half of the length of the previous arc, draw two arcs which meets each other at B.
Thus AB is the required perpendicular to .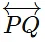

Q10: If AB = 3.6 and CD = 1.6 cm, construct a line segment equal to 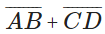and measure the total length.
Ans: Step I: Draw a ray OX.
Step II: With centre 0 and radius equal to the length of AB (3.6 cm) mark a point P on the ray.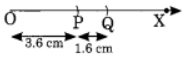
Step III: With centre P and radius equal to the length of CD (1.6 cm) mark another point Q on the ray.
Thus OQ is the required segment such that OQ = 3.6 cm + 1.6 cm = 5.2 cm.