Circles Class 9 Worksheet Maths Chapter 10
True and False
Q1: If two arc of a circle are congruent. Then corresponding chord are unequal.
Ans: False (Corresponding chords are equal)
Q2: Two perpendicular bisector of chord intersect at center of circle.
Ans: True ( each perpendicular bisector of chord passes through the center so center is common point for the two perpendicular bisectors of the chords)
Q3: The line joining the mid-point of a chord to centre perpendicular to chord.
Ans: True (A line joining the mid-point of a chord to the centre of circle, perpendicular to the chord)
Q4: It is possible to draw two circles from three non-collinear points.
Ans: False (One and only one circle can be passes through three co-linear points in a plane.)
Answer the following Questions
Q1: If O is the center of circle of radius 5 cm OP perpendicular to AB and OQ perpendicular to CD, AB||CD, AB = 6cm and CD = 8 cm. Determine PQ.
Ans: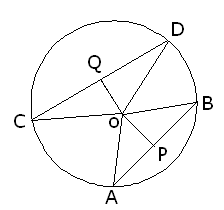 QP = OP+OQ
QP = OP+OQ
OQ ⊥ CD and OP ⊥ AB
So Q and P are mid point of Chord (A perpendicular line from centre to chord intersect at mid point.)
In ΔOPB right angled at P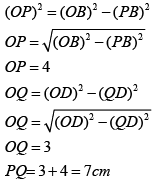
Q2: AB and CD are the two chord of the circle such that AB = 6 cm, CD = 12 cm and AB||CD, if the distance between AB and CD is 3 cm, find the radius of the circle.
Ans: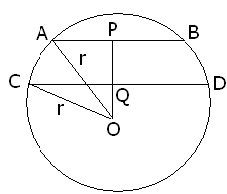 let OQ = xcm
let OQ = xcm
P and Q are the mid points of Chords in ΔAPO

Q3: Prove that the line joining to the centre of circle to the mid-point of a chord, is perpendicular to the chord.
Ans: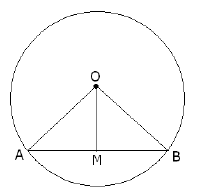 O is the centre of the circle and AB is the Chord ,OM is the line segment intersecting at M , Mid point of AB
O is the centre of the circle and AB is the Chord ,OM is the line segment intersecting at M , Mid point of AB
In ΔAMO and ΔBMO
AM = BM (M is the mid point of AB)
OA = OB (radius of circle)
OM = OM (Same side)
Hence
ΔAMO ≌ ΔBMO (By SSS)
∠AMO = ∠BMO ( BY C.P.C.T)
∠AMO +∠ BMO = 180 (linear pair angles)
∠AMO = 90
Q4: Given an arc of circle how you will find its centre and complete the circle.
Ans: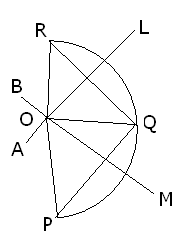 Construction :
Construction :
Step 1: Take 3 points P,Q,R on circumference of arc join P to Q and R to Q
Step 2: Draw Perpendicular bisector of line PQ and RQ these intersect at point O
Step 3: join O to P , O to Q and O to R
O is the centre of given arc where OQ and OR and OP are the radius of circle
Q5: Two equal chord AB and CD of circle with center O, when produced meet at a point E, proving that BE=DE and AE=CE
Ans: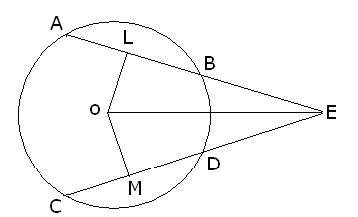 Let OL and OM be two perpendiculars from centre O to chord AB and CD respectively so L and M are the mid points of Chord AB and CD
Let OL and OM be two perpendiculars from centre O to chord AB and CD respectively so L and M are the mid points of Chord AB and CD
Since AB = CD (Given)
AB/2 = CD/2 or LB = MD
In ΔOLE and ΔOME
OL = OM (Equal Chords having equal distance from the centre)
<OLE = <OME (both 90 degree)
OE = OE (common side)
So BY R.H.S
ΔOLE ≌ ΔOME
So LE = ME ( by C.P.C.T)
LE = LB+BE
ME = MD+DE
LB+BE = MD+DE
But LB = MD (proved above)
So BE = DE
Q6: Two equal circles intersect in P and Q. A straight line through P meets the circles in A and B. prove that QA=QB
Ans: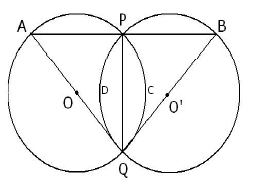 Let O and O’ be the centre of the circle where C(o, r) ≌ C(o’, r) circles are equal
Let O and O’ be the centre of the circle where C(o, r) ≌ C(o’, r) circles are equal
So PQ is the common arc in both the circle
arc(PDQ) = arc(PCQ)
<QAP = <QBP (equal chords makes equal angles on the circles)
in triangle ABQ <A = <B
so
Side AQ = Side BQ (Sides opposite to equal sides are equal)
|
44 videos|412 docs|54 tests
|
FAQs on Circles Class 9 Worksheet Maths Chapter 10
| 1. What is a circle? |  |
| 2. How is the radius of a circle determined? |  |
| 3. What is the diameter of a circle? |  |
| 4. How to calculate the circumference of a circle? |  |
| 5. Can two circles have the same circumference but different radii? |  |

|
Explore Courses for Class 9 exam
|

|

















